SPLAY or SPALY ?

写在前面：

由我们可爱的Daniel Sleator和Robert Tarjan提出的一种数据结构，平衡树的一种，本质是二叉树。

至于到底是splay还是spaly，我认为可能splay更对一些

毕竟splay是有实意的单词，更有可能一点。而且WIKI百科页也是splay

以下是本人学习splay的一点过程，请多指教喽

---

SPLAY

那么我在这里复习整理一下spaly的代码相关吧

例题：http://www.lydsy.com/JudgeOnline/problem.php?id=3224

参考博客：http://blog.csdn.net/clove_unique/article/details/50636361

 #include<cstdio>
 #define maxn 500100
 using namespace std;
 int root,N,tot;
 inline int read(){
     register int x=,t=;
     register char ch=getchar();
     while((ch<''||ch>'')&&ch!='-')ch=getchar();
     if(ch=='-'){t=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-;ch=getchar();}
     return x*t;
 }
 struct node{
     int ch[],ff,cnt,val,sum;
 }t[maxn];
 void pushup(int u){
     t[u].sum=t[t[u].ch[]].sum+t[t[u].ch[]].sum+t[u].cnt;
 }
 void rotate(int x){
     register int y=t[x].ff;
     register int z=t[y].ff;
     register int k=t[y].ch[]==x;
     t[z].ch[t[z].ch[]==y]=x;t[x].ff=z;
     t[y].ch[k]=t[x].ch[k^];t[t[x].ch[k^]].ff=y;
     t[x].ch[k^]=y;t[y].ff=x;
     pushup(y),pushup(x);
 }
 void splay(int x,int goal){
     while(t[x].ff!=goal){
         int y=t[x].ff;
         int z=t[y].ff;
         if(z!=goal)
             (t[y].ch[]==x)^(t[z].ch[]==y)?rotate(x):rotate(y);
         rotate(x);
     }
     if(goal==)
         root=x;
 }
 void insert(int x){
     int u=root,ff=;
     while(u&&t[u].val!=x){
         ff=u;
         u=t[u].ch[x>t[u].val];
     }
     if(u)
         t[u].cnt++;
     else{
         u=++tot;
         if(ff)
             t[ff].ch[x>t[ff].val]=u;
         t[tot].ch[]=;
         t[tot].ch[]=;
         t[tot].ff=ff;t[tot].val=x;
         t[tot].cnt=t[tot].sum=;
     }
     splay(u,);
 }
 void find(int x){
     int u=root;
     if(!u)return;
     while(t[u].ch[x>t[u].val]&&x!=t[u].val)
         u=t[u].ch[x>t[u].val];
     splay(u,);
 }
 int next(int x,int f){
     find(x);
     int u=root;
     if((t[u].val>x&&f)||(t[u].val<x&&!f))return u;
     u=t[u].ch[f];
     while(t[u].ch[f^])u=t[u].ch[f^];
     return u;
 }
 void del(int x){
     int la=next(x,);
     int ne=next(x,);
     splay(la,),splay(ne,la);
     int d=t[ne].ch[];
     if(t[d].cnt>){
         t[d].cnt--;
         splay(d,);
     }
     else
         t[ne].ch[]=;
 }
 int K_th(int x){
     int u=root;
     if(t[u].sum<x)
         return ;
     while(){
         int y=t[u].ch[];
         if(x>t[y].sum+t[u].cnt){
             x-=t[y].sum+t[u].cnt;
             u=t[u].ch[];
         }
         else if(t[y].sum>=x)
             u=y;
         else
             return t[u].val;
     }
 }
 int main(){
     insert(-);
     insert(+);
     N=read();
     while(N--){
         int opt=read();
         if(opt==)insert(read());
         else if(opt==)del(read());
         else if(opt==){
             find(read());
             printf("%d\n",t[t[root].ch[]].sum);
         }
         else if(opt==)printf("%d\n",K_th(read()+));
         else if(opt==)printf("%d\n",t[next(read(),)].val);
         else if(opt==)printf("%d\n",t[next(read(),)].val);
     }
     return ;
 }

上面那份代码其实是洛谷上的。。。本来想自己写的，但是怎么调都过不去5555（；´д｀）ゞ

算了吧，既然抄了代码就要抄的明明白白，这里让我们看看splay到底是怎么维护的吧

首先是一些基本操作：

1.rotate

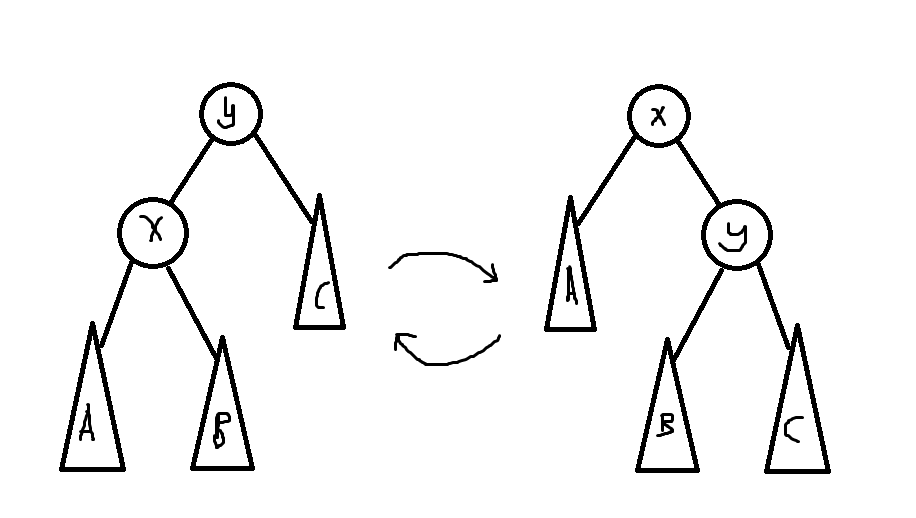
就是这个东西，保证了二叉树储存的元素顺序不变，大小顺序不变，总之转它就对了。

 void rotate(int x){
     register int y=t[x].ff;
     register int z=t[y].ff;
     register int k=t[y].ch[]==x;
     t[z].ch[t[z].ch[]==y]=x;t[x].ff=z;
     t[y].ch[k]=t[x].ch[k^];t[t[x].ch[k^]].ff=y;
     t[x].ch[k^]=y;t[y].ff=x;
     pushup(y),pushup(x);
 }

2.splay

splay是依靠平均操作来降低复杂度的，其实有点玄学，splay这个操作就是要把每次查询和修改的中心重新改变成根，

在这个过程中尽可能的让树的大小平衡，即尽可能打断原先树上存在的链，把他们压成树。。。

反正挺神的，记住写双旋时有先后就对了，尽量让树平衡。

 void splay(int x,int goal){
     while(t[x].ff!=goal){
         int y=t[x].ff;
         int z=t[y].ff;
         if(z!=goal)
             (t[y].ch[]==x)^(t[z].ch[]==y)?rotate(x):rotate(y);
         rotate(x);
     }
     if(goal==)
         root=x;
 }

em。。。接下来挑一些重点（我蒙过的）讲吧。。。

3.del
删除操作，为了精确定位我们想删掉的那个点，我们选择找到他的前驱，旋到根上，再找他的后继，旋到前驱下面

这样的话这个点只能在后继的左儿子上了

但是如果这个点没有前驱和后继岂不是药丸