石子合并问题DP

START:

2021-08-10

14:29:04

1.问题描述：

有N堆石子排成一排，每堆石子有一定的数量。现要将N堆石子并成为一堆。合并的过程只能每次将相邻的两堆石子堆成一堆，每次合并花费的代价为这两堆石子的和，经过N-1次合并后成为一堆。求出总的代价最小值。

2. 输入输出示例
输入

​ 有多组测试数据，输入到文件结束。

​ 每组测试数据第一行有一个整数n，表示有n堆石子。

​ 接下来的一行有n（0< n <200）个数，分别表示这n堆石子的数目，用空格隔开

输出

​ 输出总代价的最小值，占单独的一行

样例输入

2

3

1 2 3
7
13 7 8 16 21 4 18
样例输出

9
239

3.分析：

由题目我们可知，题目将给我们测试数据的组数，我们定义一个变量t来储存，用while(t--)来处理了这t组数据。

对于每组数据，我们首先会得到有n堆的石子，然后得到这n堆石子每堆石子的数目。

处理完数据，我们得设计算法来解题了：

对于不同的顺序，我们合并石子的代价不同。

我们举个栗子，给定4个石堆，分别有1个，2个，3个，4个石堆，我们先全部遍历一遍，比如，先只遍历长度为2的合并，看看有什么规律：

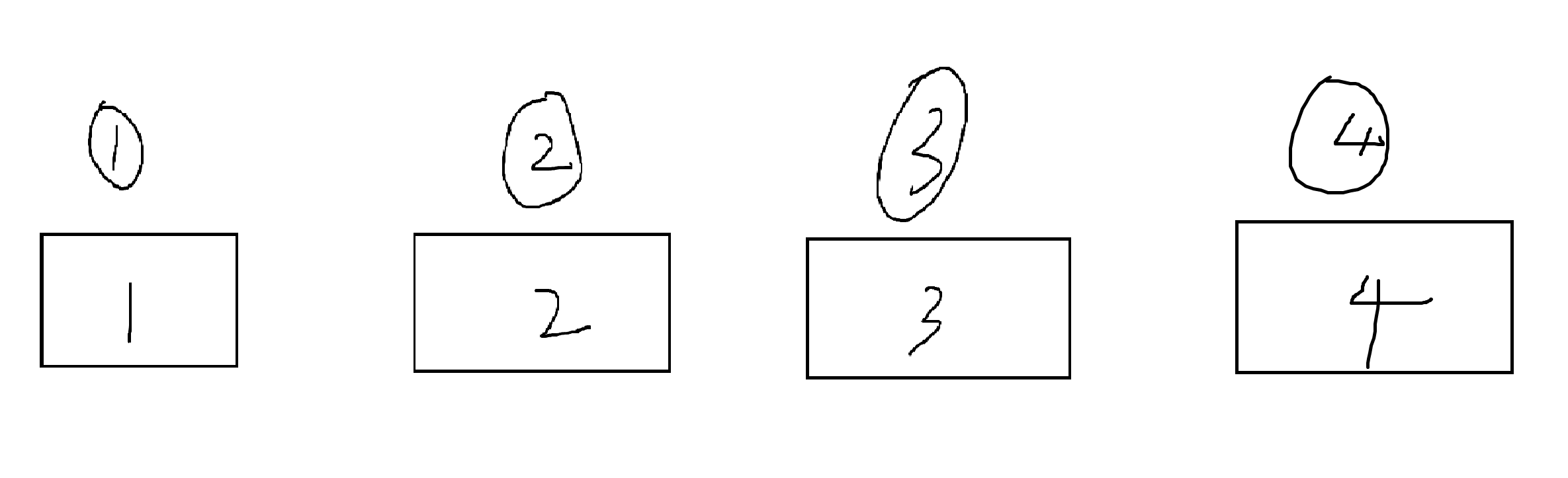
 我们可以看到，有四个石堆，分别有1个，2个，3个, 4个石头，我们先执行长度为2的合并：我们用sum[i][j]表示从i合并到j需要多少代价，dp[i][j]表示合并区间[ i , j ]的石堆累计的代价

第一种：1∪2==>sum[1][2]=1+2=3,dp[1][2]=3

第二种：2∪3==>sum[2][3]=2+3=5,dp[2][3]=5

第三种：3∪4==>sum[3][4]=3+4=7,dp[3][4]=7

我们只有四个石堆，所以合并长度为2的方案只有这三个，然后接着我们合并长度为3的：

合并区间[ 1 , 3 ]有以下两种方案：

第一种：合并{1∪2,3}，所以（1∪2）∪3：

sum[1][3]=sum[1][2]+sum[3][3]=3+3=6

dp[1][3]=sum[1][2]+sum[1][3]=3+6=9

第二种：合并{1,2∪3}，所以1∪（2∪3）：

sum[1][3]=sum[1][1]+sum[2][3]=1+5=6

dp[1][3]=sum[2][3]+sum[1][3]=5+6=11

所以合并区间[1,3]的最优方案是先合并1,2再合并3。

由此我们知道，合并区间[i,j]的最小代价是由：

已经有的合并代价最小值dp[i][j]，和从i 到k的最小代价、从k+1到j的最小代价、从i到j的合并代价的和取最小值

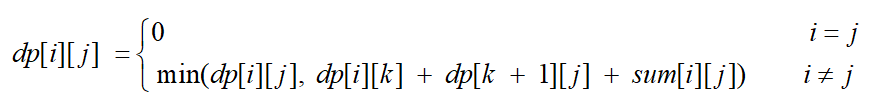
 程序结构：

关于核心函数solve()，我们该怎么写，我们程序结构里一共有三层for循环:

最外层循环是循环枚举合并长度，从1~n-1

第二层循环是循环枚举每次合并长度固定的时候的起点

第三层循环是循环枚举合并区间固定时，分界线的位置。

其实这个做法的核心不是看合并区间的长度和起点的位置，而是最后一层的分界线的位置：

因为对于每种合并，都有分界线，那么最后一次合并的时候，一定有一个最终分界线，我们最小代价就是在这道分界线上取得的。

对于状态转移公式：dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[i][j])，我们一定要确保我们在计算dp[i][j]的时候，

dp[i][k],dp[k+1][j],sum[i][j]都是已经计算好了的。

for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        s[i] += s[i - 1] + a[i];
    }

    // 区间 DP 枚举套路：长度+左端点
    for (int len = 1; len < n; len ++) { // len表示i和j堆下标的差值
        for (int i = 1; i + len <= n; i ++) {
            int j = i + len; // 自动得到右端点
            dp[i][j] = 1e8;
            for (int k = i; k <= j - 1; k ++) { // 必须满足k + 1 <= j
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);
            }
        }
    }

最后输出dp[1][n]就行了

END:

2021-08-10

15:43:10