Lecture 1. Introduction and Basics - Carnegie Mellon - Computer Architecture 2015 - Onur Mutlu

1.Hamming Distance: 两个相同长度比特串对应位置的不同位的数量，一般使用 d(x,y) 来表示汉明距离。对两个比特串进行异或运算，统计结果为1的个数就是汉明距离。

 

============= 一个问题：内存独占问题 ============

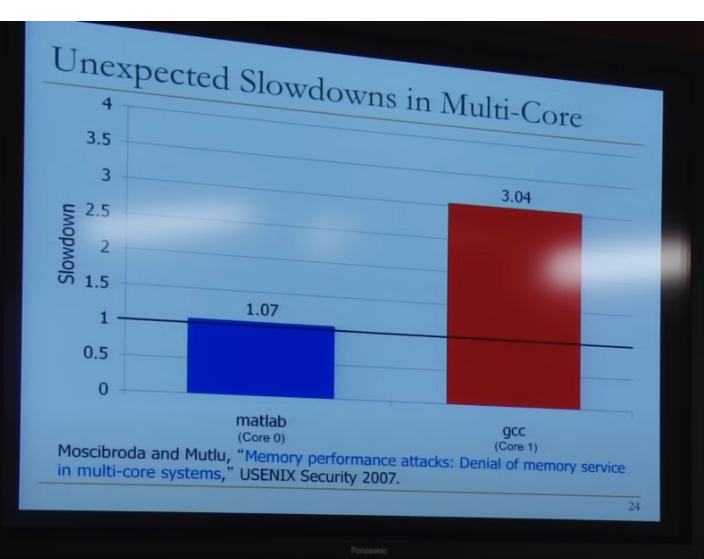
做个实验，core0运行matlab，core1运行gcc，统计它们的运行时长

matlab的运行时长是只运行matlab时的1.07倍

gcc的运行时长是只运行gcc时的3.04倍

为什么呢？

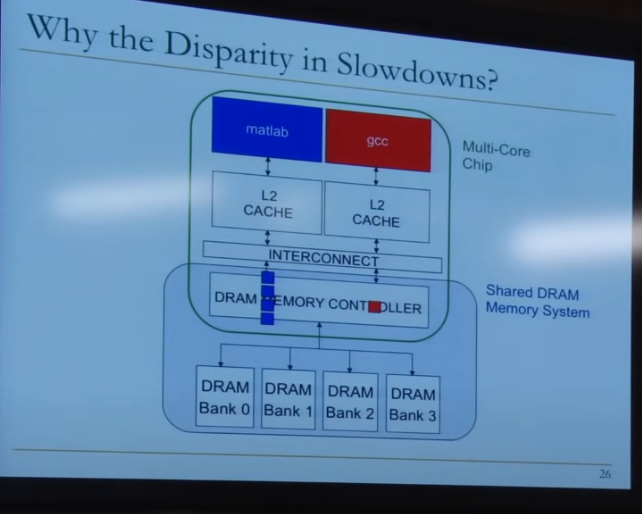
在matlab和gcc的内存访问请求发送到 DRAM Controller 时，由于Matlab的内存访问请求具有高度 locality，因此内存控制器会优先处理Matlab的内存访问请求（性能优化）

如图是一种很经典的内存访问优化方法，使用 Row Buffer 读取 DRAM，一次读取一行。

当下一个内存访问请求到来时，如果属于同一行内存，直接从 Row buffer 拿出去

如果不是属于同一行内存，那么Row buffer 就要重新从 DRAM 读取内容

在外面，DRAM controller，或者别的什么东西，会对内存访问请求进行排序，来优化内存访问速度。

因此，可以料想，gcc的内存访问请求被DRAM controller往后排序了，因此gcc会慢得多

但这种性能优化策略也会带来问题：如下

这是内存独占。

由于STREAM程序的row buffer locality远比RANDOM程序要好，因此DRAM controller总是优先处理STREAM的内存访问请求，因此STREAM某种程度上成为了RANDOM的DDOS攻击

当然了，这种情形有一个前提：Memory Request Buffer 要足够大

======== 另一个问题：DRAM的Refresh Overhead =============

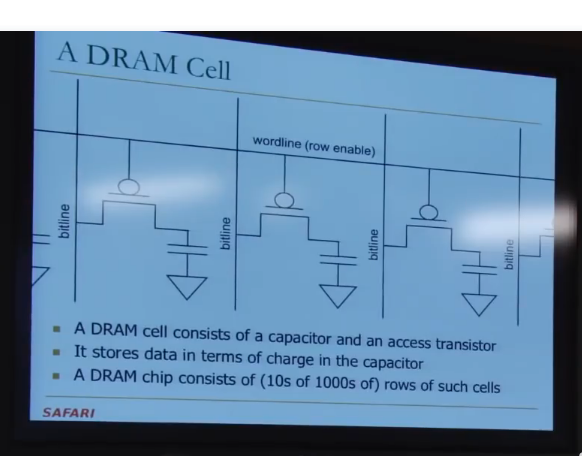
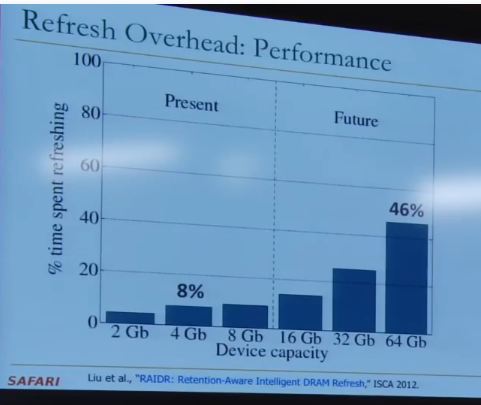
DRAM的刷新时间被设置成了64ms，但DRAM中并不是每一行Cell都无法保存超过64ms的数据。

仅仅只有一少部分Cell保存数据的时长在64-128ms

另外很少一部分Cell保存数据的时长在128-256ms

大部分Cell保存数据的时长是大于256ms的。

为了保守起见（毕竟在生产时，并非每个DRAM Cell都是一样的），我们才把Refresh gap定为 64ms

如果我们能把 memory row retention time 暴露给上层，那么是不是就可以仅对一部分memory row进行64ms 的refresh，而对其它的memory row进行间隔更长的refresh了？

这里有三个问题：

1. 这些信息暴露给谁？

2. 暴露多少信息

3. 如何确定每一行memory row的 retention time? (毫无疑问，这是最难的部分)

如图，是三星公司的一个工作。

分为三步骤：

1. 计算每一行内存的retention time（最难的部分）

2. 根据 retention time 给每一行内春的行号分配桶 (使用 Bloom Filters)

3. Memory Controller，根据不同的桶，给不同的桶的内存行用不同的刷新频率来刷新

结果：性能提升、功耗降低

似乎是一篇很棒的paper？不过我暂时不打算去读

两个很好用的建议？

============== 第三个问题：Row hammer ==============

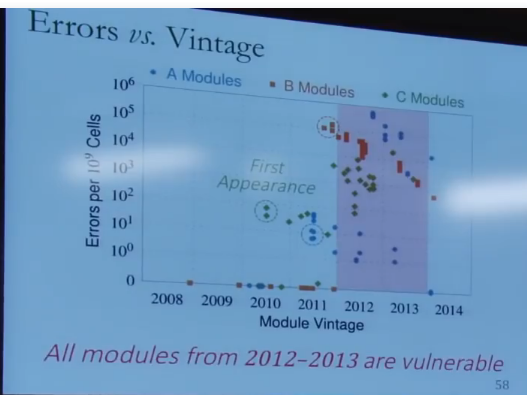
Rowhammer对2012-2013的内存最有效，而对2014以后的内存就没什么作用了

三种可能的解决方向（so..l.解决方案并没有公布？）