fzy&czn生日赛t1 CZN

fzy&czn生日赛t1 CZN

膜拜hybb首杀

目录

• fzy&czn生日赛t1 CZN
  • 题目背景
  • 题目描述
  • 分析
  • my code
  • wnag's code

题目

题目背景

有一天，czn在机房里面心心念念的pj终于来找他了，pj希望czn能够帮助她来解决一道数学题，czn“十分不乐意”地接下了这个题目，所以他希望你可以帮助他一下。

题目描述

\(\\\) 不等式是形如 \((x - a_1)^{b_1} * (x - a_2)^{b_2} * (x - a_3)^{b_3} * ······ * (x - a_n)^{b_4} < 0\) 的式子，

\(\\\) 请问这个不等式关于 \(x\) 的解集是多少？

分析

我们把不等式的每一项拆开看，只要满足小于0的项有奇数个不等式就成立且任意一想不等式均不等于 \(0\) 。

朴素算法是判断每一个区间是否成立。

简便一点的做法就是：穿根法。

对于这个数据：

5
13 21 9 70 22
23 36 8 29 15

我们把所有 \(a_i\) 从小到大排序

9 13 21 22 70
8 23 36 15 29

然后画在数轴上，如下：

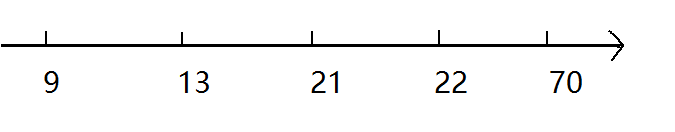
之后我们从右上方开始穿针引线，如果第 $b_i \ mod \ 2 == 0 $ 就穿过它，如下：

最后我们发现在数轴之下的区间都是合法的，再处理一下所有区间都不包含端点就可以了。

记得开\(long\ long\)

my code

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define LL long long
using namespace std;
const int INF = -114514 , N = 1e5 + 5;
int ans[N][5] , n , ans1;
struct R {
    LL a , b;
}re[N];
bool comp (R x , R y) { return x.a < y.a; }
int main () {
    scanf ("%d" , &n);
    re[1].a = INF , re[1].b = 1;
    fu (i , 2 , n + 1) {
        scanf ("%lld" , &re[i].a);
    }
    fu (i , 2 , n + 1)
        scanf ("%lld" , &re[i].b);
    sort (re + 2 , re + n + 2 , comp);
    int i = n + 1;
    while (i >= 1) {
        while (re[i].b % 2 == 0 && i >= 1)
            i --;
        if (i <= 1) break;
        ans[++ans1][1] = i , ans[ans1][2] = i - 1;
        i --;
        while (re[i].b % 2 == 0 && i >= 1) {
            ans[++ans1][1] = i , ans[ans1][2] = i - 1;
            i --;
        }
        i --;
    }
    if (!ans1) {
        printf ("NO ANSWER") , exit (0);
    }
    printf ("%d\n" , ans1);
    for (int i = ans1 ; i >= 1 ; i --) {
        if (re[ans[i][2]].a != INF)
            printf ("%lld<x<%lld\n" , re[ans[i][2]].a , re[ans[i][1]].a);
        else
            printf ("-INF<x<%lld\n" , re[ans[i][1]].a);
    }
    return 0;
}

wnag's code

#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL n,tot=0;
struct node
{
    LL a,b;
}s[100000+10],fans[100000+10];
bool cmp(node a,node b)
{
    return a.a<b.a;
}
int main()
{
    scanf("%lld",&n);
    for(int i=1;i<=n;++i)
        scanf("%lld",&s[i].a);
    for(int i=1;i<=n;++i)
        scanf("%lld",&s[i].b);
    sort(s+1,s+n+1,cmp);
    int y=0;
    for(int i=n;i>=1;--i)
    {
        while(s[i].b%2==0&&i>=1)
            i--;
        if(i==0)
            break;
        y=s[i].a;
        i--;
        while(s[i].b%2==0&&i>=1)
        {
            fans[++tot]=(node){s[i].a,y};
            y=s[i].a;
            i--;
        }
        if(i==0)
            fans[++tot]=(node){0,y};
        else
            fans[++tot]=(node){s[i].a,y};
    }
    sort(fans+1,fans+tot+1,cmp);
    if(tot==0)
        printf("NO ANSWER");
    else
    {
        printf("%lld\n",tot);
        for(int i=1;i<=tot;++i)
        {
            if(fans[i].a==0)
                printf("-INF<x<%lld\n",fans[i].b);
            else
                printf("%lld<x<%lld\n",fans[i].a,fans[i].b);
        }
    }
    return 0;
}