【算法学习笔记】区间DP

基本的知识点引用自 OI wiki，感谢社区的帮助

什么是区间 DP？

区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。令状态 \(f(i,j)\) 表示将下标位置 \(i\) 到 \(j\) 的所有元素合并能获得的价值的最大值，那么 \(f(i,j)=\max\{f(i,k)+f(k+1,j)+cost\}\)，\(cost\) 为将这两组元素合并起来的代价。

区间 DP 的特点：

合并：即将两个或多个部分进行整合，当然也可以反过来；

特征：能将问题分解为能两两合并的形式；

求解：对整个问题设最优值，枚举合并点，将问题分解为左右两个部分，最后合并两个部分的最优值得到原问题的最优值。

例题「NOI1995」石子合并

在一个环上有 $n$ 个数 $a_1,a_2,...,a_n$，进行 $n-1$ 次合并操作，每次操作将相邻的两堆合并成一堆，能获得新的一堆中的石子数量的和的得分。你需要最大化你的得分。

正常来说考虑不在环上，而在一条链上的情况。

令 \(f(i,j)\) 表示将区间 \([i,j]\) 内的所有石子合并到一起的最大得分。

写出 状态转移方程：

\[f(i,j)=\max\{f(i,k)+f(k+1,j)+\sum_{t=i}^{j} a_t \}~(i\le k
\]

令 \(sum_i\) 表示 \(a\) 数组的前缀和，状态转移方程变形为

\[f(i,j)=\max\{f(i,k)+f(k+1,j)+sum_j-sum_{i-1}\}
\]

怎样进行状态转移

由于计算 \(f(i,j)\) 的值时需要知道所有 \(f(i,k)\) 和 \(f(k+1,j)\) 的值，而这两个中包含的元素的数量都小于 \(f(i,j)\)，所以我们以 \(len=j-i+1\) 作为 DP 的阶段。首先从小到大枚举 \(len\)，然后枚举 \(i\) 的值，根据 \(len\) 和 \(i\) 用公式计算出 \(j\) 的值，然后枚举 \(k\)，时间复杂度为 \(O(n^3)\)

怎样处理环

题目中石子围成一个环，而不是一条链，怎么办呢？

方法一：由于石子围成一个环，我们可以枚举分开的位置，将这个环转化成一个链，由于要枚举 \(n\) 次，最终的时间复杂度为 \(O(n^4)\)。

方法二：我们将这条链延长两倍，变成 \(2\times n\) 堆，其中第 \(i\) 堆与第 \(n+i\) 堆相同，用动态规划求解后，取 \(f(1,n),f(2,n+1),...,f(i,n+i-1)\) 中的最优值，即为最后的答案。时间复杂度 \(O(n^3)\)。

核心代码

for (len = 1; len <= n; len++)
    for (i = 1; i <= 2 * n - 1; i++) {
        int j = len + i - 1;
        for (k = i; k < j && k <= 2 * n - 1; k++)
            f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j] + sum[j] - sum[i - 1]);
    }

---

分析方法和模版

---

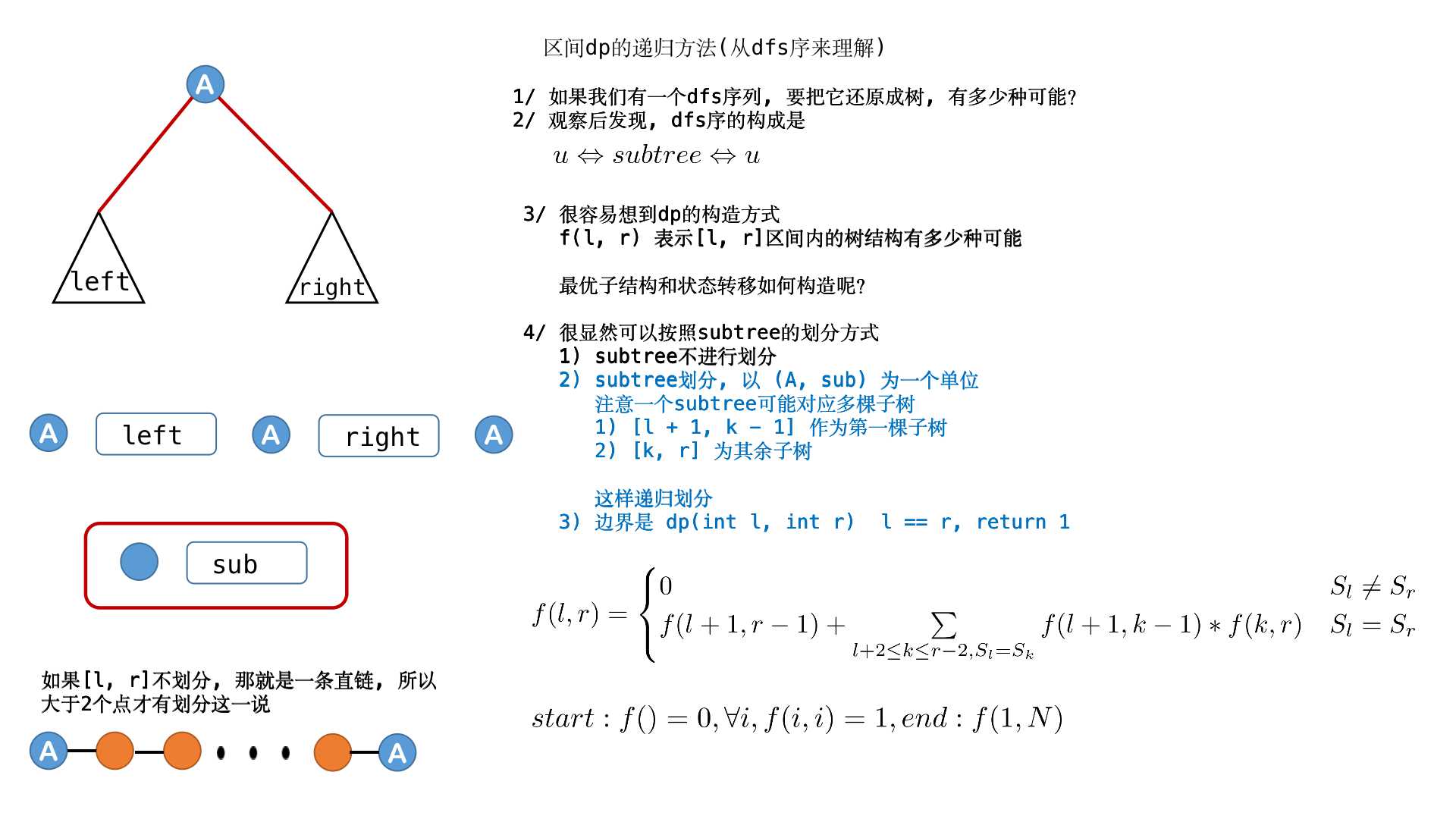
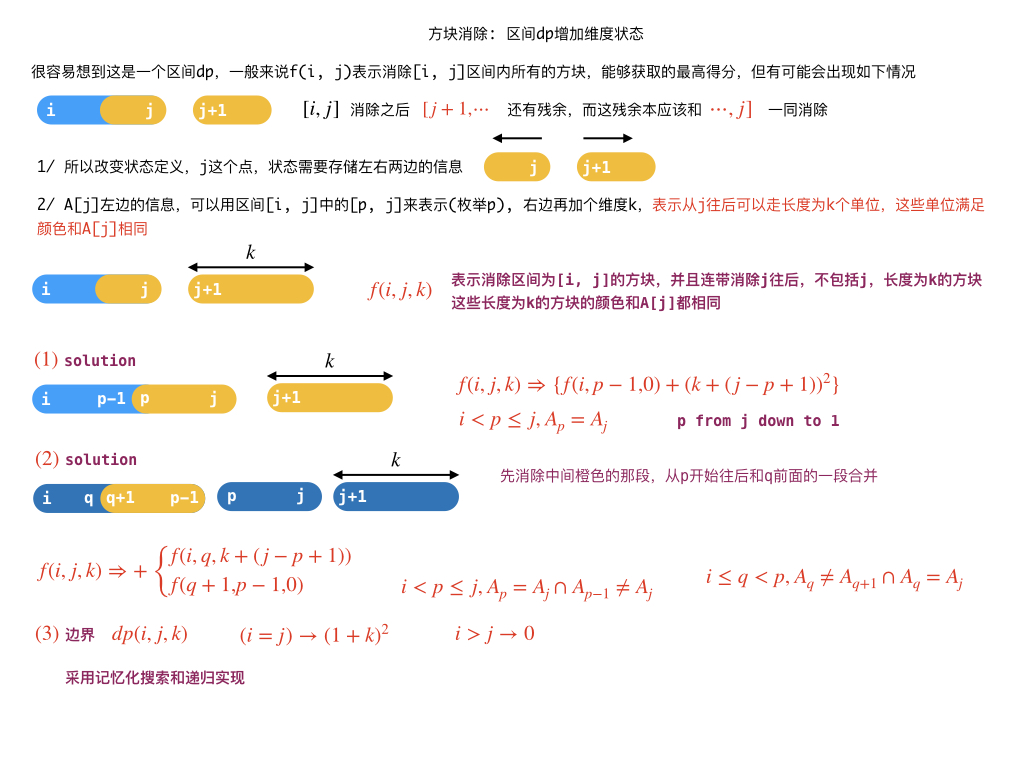
区间DP 练习题题解 ①：Here

区间DP 练习题题解 ②：Here