Luogu P1298 最接近的分数 做题记录

算是水紫，不过也学到一些有用的东西。

---

题意

给定正小数 \(N\)。求分子不大于 \(n\)，分母不大于 \(m\) 的分数 \(\dfrac{n}{m}\)，使得 \(\dfrac{n}{m}\) 的值与 \(N\) 最接近（这里的最接近指的是 \(|\dfrac{n}{m} - N|\) 最小）。

分析

首先，大部分人都可以想到一个暴力：枚举 \(i \in [1, m]\) 作为分子，计算出最佳分母 \(r_1 = \lfloor i \times N \rfloor, r_2 = \lceil i \times N\rceil\)。把 \(r_1, r_2\) 分别带进去看看那个更优就完事了。出去判边界之类的问题，复杂度 \(O(m)\)。由于 \(m \leq 10 ^ 7\)，直接就艹过去了。如果这个都不会写可以看这里：暴力算法。

然而我们肯定不会满足于这样的暴力算法。来点优雅的算法吧。

---

引入分数逼近。这里的分数逼近是指用用一个分数来逼近另一个分数，使得误差趋于零。例如，假设需要逼近的分数为 \(\dfrac{r}{s}\)，有分数 \(\dfrac{u}{v} > \dfrac{r}{s}\)。那么有以下结论：

\[\dfrac{r}{s} \leq \dfrac{r + u}{s + v} \leq \dfrac{u}{v}
\]

具体等号能不能取到记不清了，不过不影响。结论很好证明，下面证一下。

---

将 \(\dfrac{r + u}{s + v}\) 与 \(\dfrac{r}{s}\) 做减法，得到 \(\dfrac{r + u}{s + v} - \dfrac{r}{s} = \dfrac{(r + u)s - r(s + v)}{s(s + v)} = \dfrac{us- vr}{s(s + v)}\)。

因为 \(\dfrac{r}{s} < \dfrac{u}{v}\)，两边同时乘以 \(sv\)，得 \(vr < us\)，即 \(us - vr > 0\)。

又因为 \(s(s + v) > 0\)，所以 \(\dfrac{us - vr}{s(s + v)} > 0\)。证毕。

注意上面结论和证明成立的条件是 \(u, v, s, r > 0\)。

---

接下来引入 Stern-Brocot 树这个概念。

Stern-Brocot 树可以维护所有的正分数。这一点可以被我们用来解决这道题目。

首先介绍一下 Stern-Brocot 树。这个树由 \(\dfrac{0}{1}\) 和 \(\dfrac{1}{0}\) 两个分数开始。\(\dfrac{1}{0}\) 不大好定义，暂且把它当做 \(+ \infty\)。将这两个分数作为源节点。

接下来，像我们刚才讨论的分数逼近，将 \(\dfrac{0}{1}\) 和 \(\dfrac{1}{0}\) 的分子分母分别相加，得到另外一个分数 \(\dfrac{1}{1}\)。这个分数确实在 \(\dfrac{0}{1}\) 与 \(\dfrac{1}{0}\) 之间。\(\dfrac{1}{1}\) 被成为第 \(1\) 层迭代后的节点。

同样的，将 \(\dfrac{1}{1}\) 与 \(\dfrac{0}{1}, \dfrac{1}{0}\) 分别进行操作，得到两个分数，称为第二次迭代。

所以我们得到了 Stern-Brocot 树的构建基础：将 \(\dfrac{a}{b}\) 与 \(\dfrac{c}{d}\) 分子分母分别相加，得到 \(\dfrac{a + c}{b + d}\) 作为下一轮迭代的节点。

例如，进行三次操作后，这棵树就会变成这样：

\[\begin{array}{c} \dfrac{0}{1}, \dfrac{1}{1}, \dfrac{1}{0} \\\\ \dfrac{0}{1}, \dfrac{1}{2}, \dfrac{1}{1}, \dfrac{2}{1}, \dfrac{1}{0} \\\\ \dfrac{0}{1}, \dfrac{1}{3}, \dfrac{1}{2}, \dfrac{2}{3}, \dfrac{1}{1}, \dfrac{3}{2}, \dfrac{2}{1}, \dfrac{3}{1}, \dfrac{1}{0} \end{array}
\]

注意，某些节点（就是第 \(i\) 层存在，第 \(i + 1\) 层也存在的节点），实际上在第 \(i + 1\) 层是不会出现的。只是为了方便比较加了上去。

可以看到，第三层的第二个分数 \(\dfrac{1}{3}\) 就是左右两边两个数分子分母分别相加的和。第四个，第六个和第八个以此类推。

下面是来自 OI-wiki 的一张图。

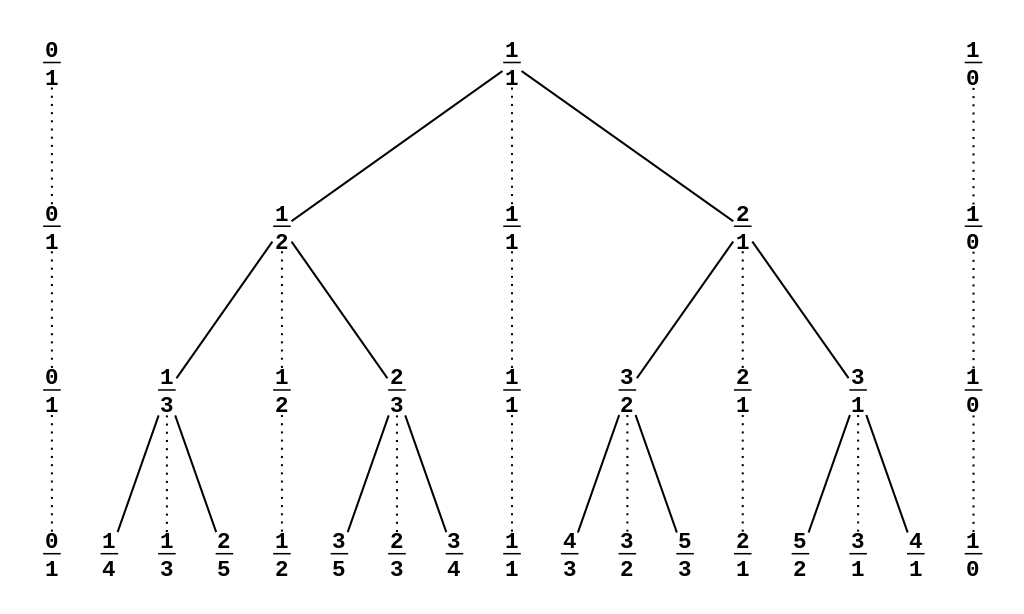
刚才所提到的不存在的节点就是虚线相连的那些节点。可以看到，这棵树具有二叉结构。因此在这棵树上搜索只需要花费 \(O(\log_2 n)\) 的时间。非常优秀。这样对于这道题，我们就可以把小数 \(N\) 从第一层开始向下搜索。如果当前节点值大于 \(N\)，那么向左递归。否则向右递归，直到分子或分母大于 \(n\) 或 \(m\)。时间复杂度肯定是 \(O(\log n)\)。（假设 \(n, m\) 同阶）。

关于最简性的证明可以看 OI-wiki 上的解释。这里不再赘述。

---

这道题的思路就讲解完了。注意别忘了判断多解的情况。由于刚才提到，Stern-Brocot 树具有最简性，因此放心的判断当前分数值与 \(N\) 的误差和原来的是否一样就可以了。

卡常顺便卡了个 rank1。欢迎来踩。

代码

#include <algorithm>
#include <cstdio>

using PII = std::pair<int, int>;
double N, m_error;
int n, m;
PII ans(0, 1);
bool flag = false;

double fabs(double x) {
    return x < 0 ? -x : x;
}
inline void get(double N, int a = 0, int b = 1, int c = 1, int d = 0) {
	int x = a + c, y = b + d;
	if (x > n || y > m) return;
	double error = (double)x / y - N;
	if (fabs(error) == m_error) flag = true;
	if (fabs(error) < m_error) {
		flag = false; ans = {x, y}; m_error = fabs(error);
		if (error == 0) return;
	}
	if (error < 0) get(N, x, y, c, d);
	else get(N, a, b, x, y);
}

int main() {
	scanf("%d%d", &n, &m);
	scanf("%lf", &N); m_error = N; get(N);
	if (flag) puts("TOO MANY");
	else printf("%d/%d", ans.first, ans.second);
	return 0;
}

明天就是五一劳动节。在这里提前祝大家五一快乐，多多点赞。