2023-09-23：用go语言，假设每一次获得随机数的时候，这个数字大于100的概率是P。 尝试N次，其中大于100的次数在A次~B次之间的概率是多少? 0 ＜ P ＜ 1, P是double类型，

2023-09-23：用go语言，假设每一次获得随机数的时候，这个数字大于100的概率是P。

尝试N次，其中大于100的次数在A次~B次之间的概率是多少?

0 < P < 1, P是double类型，

1 <= A <= B <= N <= 100。

来自左程云。

答案2023-09-23：

首先，我们可以使用动态规划来解决这个问题。我们可以定义一个二维数组dp，其中dp[i][j]表示在i次尝试中，获得j次大于100的随机数的概率。

然后，我们可以使用递归的方式计算dp[i][j]。具体地说，我们可以将每一次尝试分为两种情况：获得大于100的随机数和获得小于等于100的随机数。如果我们获得大于100的随机数，则剩余的i-1次尝试中，我们需要获得j-1次大于100的随机数；如果我们获得小于等于100的随机数，则剩余的i-1次尝试中，我们还需要获得j次大于100的随机数。我们可以使用更大的P表示获得大于100的随机数的概率，用1-P表示获得小于等于100的随机数的概率。

递归的边界条件是如果i为0且j为0，则表示已经没有剩余的尝试次数，并且已经获得了所需的j次大于100的随机数，所以概率为1；如果i为0且j不为0，则表示已经没有剩余的尝试次数，但是还没有满足所需的j次大于100的随机数，所以概率为0。

为了避免重复计算，我们可以使用一个二维数组dp来保存计算过的结果。在每次计算前，先检查dp[i][j]是否已经计算过，如果是，则直接返回结果。

最后，在主函数中，我们可以调用probability函数来计算概率，并打印结果。

总的时间复杂度和额外空间复杂度分别为O(N^2)，因为需要计算dp数组的所有元素。

go完整代码如下：

package main

import "fmt"

func probability(P float64, N int, A int, B int) float64 {
	dp := make([][]float64, N+1)
	for i := 0; i <= N; i++ {
		dp[i] = make([]float64, N+1)
		for j := 0; j <= N; j++ {
			dp[i][j] = -1
		}
	}
	ans := 0.0
	for j := A; j <= B; j++ {
		ans += process(P, 1-P, N, j, dp)
	}
	return ans
}

func process(more, less float64, i, j int, dp [][]float64) float64 {
	if i < 0 || j < 0 || i < j {
		return 0
	}
	if i == 0 && j == 0 {
		return 1
	}
	if dp[i][j] != -1 {
		return dp[i][j]
	}
	ans := more*process(more, less, i-1, j-1, dp) + less*process(more, less, i-1, j, dp)
	dp[i][j] = ans
	return ans
}

func main() {
	P := 0.6
	N := 100
	A := 30
	B := 50
	fmt.Println(probability(P, N, A, B))
}

rust完整代码如下：

fn probability(p: f64, n: i32, a: i32, b: i32) -> f64 {
    let mut dp: Vec<Vec<f64>> = vec![vec![-1.0; (n + 1) as usize]; (n + 1) as usize];
    let mut ans = 0.0;
    for j in a..=b {
        ans += process(p, 1.0 - p, n, j, &mut dp);
    }
    ans
}

fn process(more: f64, less: f64, i: i32, j: i32, dp: &mut Vec<Vec<f64>>) -> f64 {
    if i < 0 || j < 0 || i < j {
        return 0.0;
    }
    if i == 0 && j == 0 {
        return 1.0;
    }
    if dp[i as usize][j as usize] != -1.0 {
        return dp[i as usize][j as usize];
    }
    let ans = more * process(more, less, i - 1, j - 1, dp) + less * process(more, less, i - 1, j, dp);
    dp[i as usize][j as usize] = ans;
    ans
}

fn main() {
    let p = 0.6;
    let n = 100;
    let a = 30;
    let b = 50;
    println!("{}", probability(p, n, a, b));
}

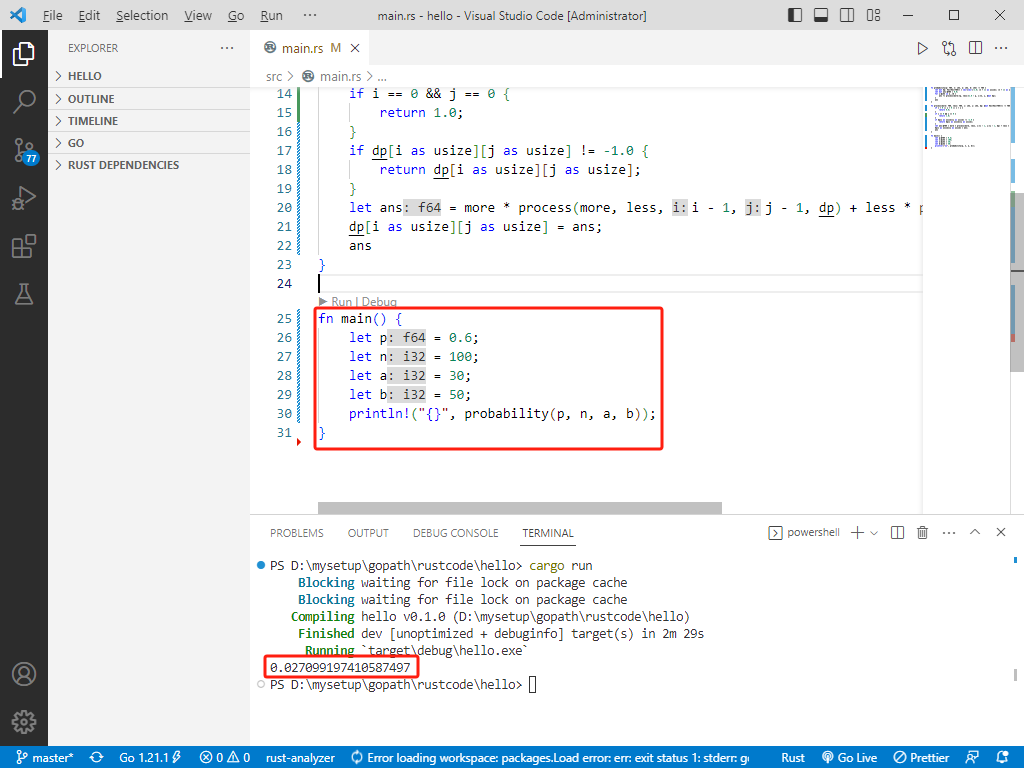
c++完整代码如下：

#include <iostream>
#include <vector>

double process(double more, double less, int i, int j, std::vector<std::vector<double>>& dp);

double probability(double P, int N, int A, int B) {
    std::vector<std::vector<double>> dp(N + 1, std::vector<double>(N + 1, -1));
    double ans = 0;
    for (int j = A; j <= B; j++) {
        ans += process(P, 1 - P, N, j, dp);
    }
    return ans;
}

double process(double more, double less, int i, int j, std::vector<std::vector<double>>& dp) {
    if (i < 0 || j < 0 || i < j) {
        return 0;
    }
    if (i == 0 && j == 0) {
        return 1;
    }
    if (dp[i][j] != -1) {
        return dp[i][j];
    }
    double ans = more * process(more, less, i - 1, j - 1, dp) + less * process(more, less, i - 1, j, dp);
    dp[i][j] = ans;
    return ans;
}

int main() {
    double P = 0.6;
    int N = 100;
    int A = 30;
    int B = 50;
    std::cout << probability(P, N, A, B) << std::endl;
    return 0;
}

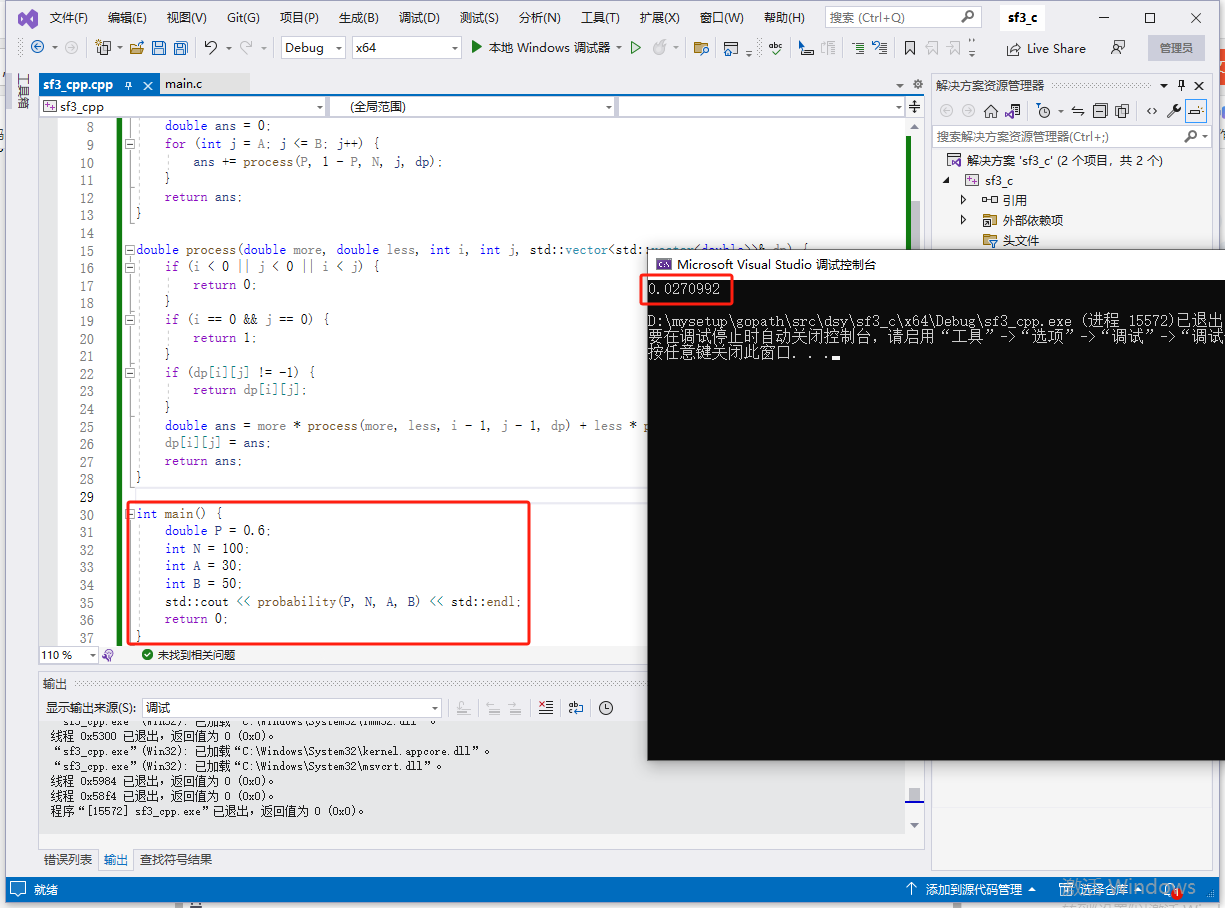
c完整代码如下：

#include <stdio.h>
#include <stdlib.h>

double probability(double P, int N, int A, int B);
double process(double more, double less, int i, int j, double** dp);

double probability(double P, int N, int A, int B) {
    double** dp = (double**)malloc((N + 1) * sizeof(double*));
    for (int i = 0; i <= N; i++) {
        dp[i] = (double*)malloc((N + 1) * sizeof(double));
    }

    for (int i = 0; i <= N; i++) {
        for (int j = 0; j <= N; j++) {
            dp[i][j] = -1;
        }
    }

    double ans = 0;
    for (int j = A; j <= B; j++) {
        ans += process(P, 1 - P, N, j, dp);
    }

    for (int i = 0; i <= N; i++) {
        free(dp[i]);
    }
    free(dp);

    return ans;
}

double process(double more, double less, int i, int j, double** dp) {
    if (i < 0 || j < 0 || i < j) {
        return 0;
    }

    if (i == 0 && j == 0) {
        return 1;
    }

    if (dp[i][j] != -1) {
        return dp[i][j];
    }

    double ans = more * process(more, less, i - 1, j - 1, dp) + less * process(more, less, i - 1, j, dp);
    dp[i][j] = ans;
    return ans;
}

int main() {
    double P = 0.6;
    int N = 100;
    int A = 30;
    int B = 50;
    printf("%f\n", probability(P, N, A, B));

    return 0;
}