机器学习数学|微积分梯度jensen不等式

机器学习中的数学

觉得有用的话,欢迎一起讨论相互学习~Follow Me

原创文章,如需转载请保留出处

本博客为七月在线邹博老师机器学习数学课程学习笔记

索引

• 微积分,梯度和Jensen不等式
• Taylor展开及其应用
• 常见概率分布和推导
• 指数族分布
• 共轭分布
• 统计量
• 矩估计和最大似然估计
• 区间估计
• Jacobi矩阵
• 矩阵乘法
• 矩阵分解RQ和SVD
• 对称矩阵
• 凸优化

微积分与梯度

• 常数e的计算过程
• 常见函数的导数
• 分部积分法及其应用
• 梯度
• 上升/下降最快方向
• 凸函数
• Jensen不等式

---

自然常数e

引入

• 我们知道对于公式\(y=log_{a}x\),x=1时,y=0.则我们是否能找一点a值,使得y函数在(1,0)点的导数为1呢?

  利用导数公式对\(y=log_{a}x\)求导

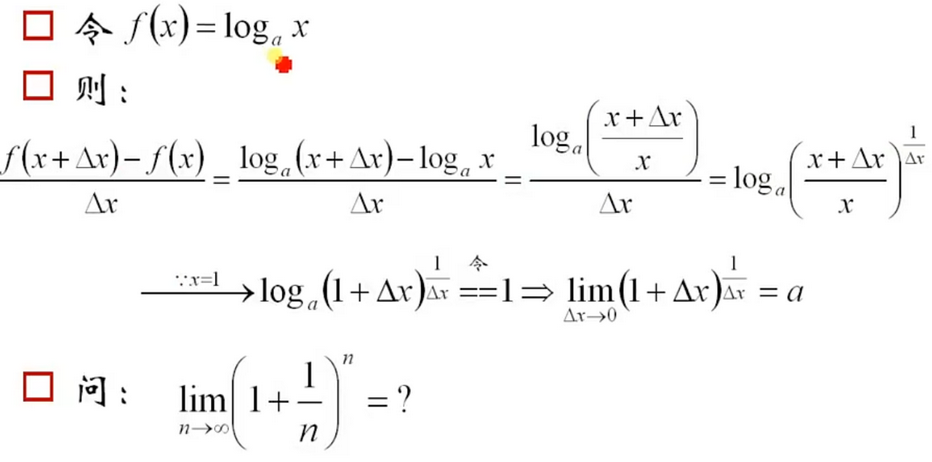
定理一:极限存在定理

• 单调有界函数必有极限
• 单调数列有上线,必有其极限

构造数列Xn证明其单调有上界

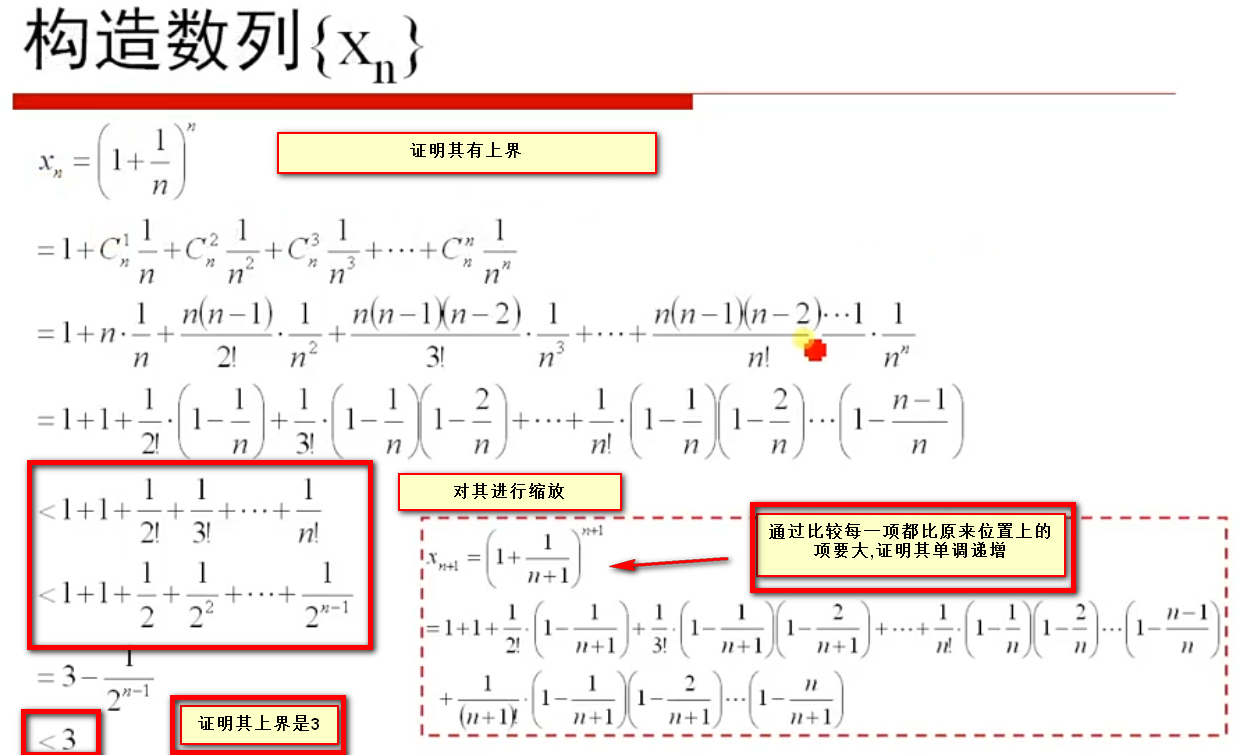
• 又因为其有(1+1)项,则其必比2要大然而又比3要小,则\(2<X_n<3\)

定理二:两边夹定理

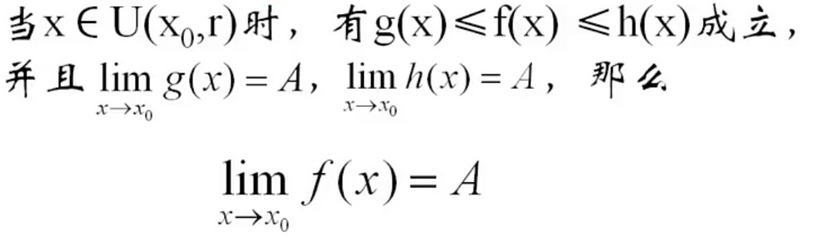
自然常数e的推导

• \[自然常数e可以看做e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...+\frac{1}{n!}\]

---

微分与积分

常用函数的导数公式

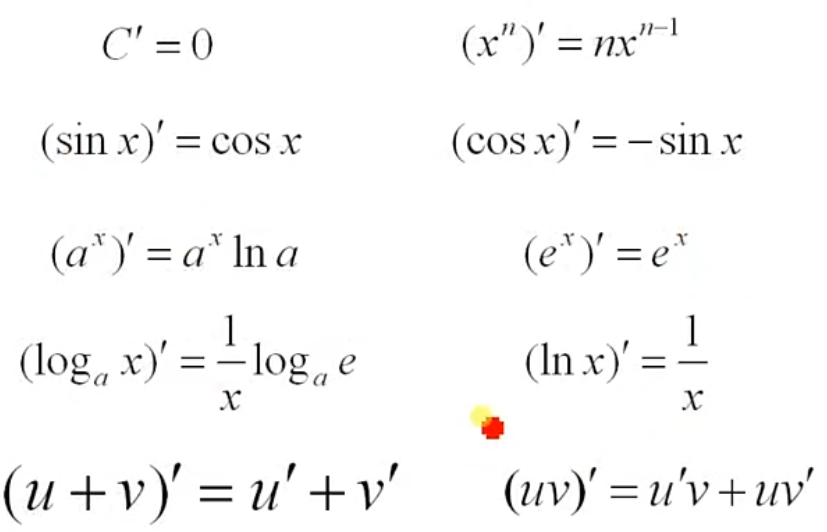
分部积分法

方向导数与梯度

对于方向导数我们也可以视为\[(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}).(cos\varphi.sin\varphi)^{T}\]方向导数顾名思义既是复合函数在某一方向上的导数，表示函数在某一方向上的变化趋势。当在某一方向上的方向导数最大时，即是梯度 当 \[cos\varphi =\frac{\partial f}{\partial x}\\sin\varphi = \frac{\partial f}{\partial y}\] 时,这是方向导数取最大值,即是梯度

对于梯度我们有

• 方向导数是各个方向上的导数
• 偏导数连续才有梯度存在
• 梯度的方向是方向导数中取到最大值的方向，梯度的值是方向导数的最大值

---

凸函数与Jsnsen不等式

• 简而言之,即是函数的割线永远位于函数图像的上方.

一阶可微

• 简而言之,即是函数如果是一个凸函数,且一阶可微,则过函数任意一点做函数的切线,函数的切线永远在函数的下方.

二阶可微

凸函数举例

Jensen不等式

• Jensen不等式相当于把凸函数的概念反过来说,即是如果f是一个凸函数,任意取一个在f定义域上的(x,y)点,\(\theta\)属于[0,1].
• 当只有x,y两个参数,即是使用 基本Jensen不等式 ,然而当推广到k个参数时, 即是表示参数的线性加权的函数值总要小于函数值的线性加权.
• 可以将其推广到概率密度分布上,假设\(\theta\)表示是事件的概率密度K点分布即所加和为1,则函数值的期望大于期望的函数值

PS:这都是在f是凸函数的状况下!

• Jensen不等式是所有不等式的基础,所有不等式都能看做是Jensen不等式利用不同的凸函数推导出来的.

课程传送门