决策树--CART树详解
1.CART简介
CART是一棵二叉树,每一次分裂会产生两个子节点。CART树分为分类树和回归树。
分类树主要针对目标标量为分类变量,比如预测一个动物是否是哺乳动物。
回归树针对目标变量为连续值的情况,比如预测一个动物的年龄。
如果是分类树,将选择能够最小化分裂后节点GINI值的分裂属性;
如果是回归树,选择能够最小化两个节点样本方差的分裂属性。CART跟其他决策树算法一样,需要进行剪枝,才能防止算法过拟合从而保证算法的泛化性能。
2.CART分类树
2.1算法详解
CART分类树预测分类离散型数据,采用基尼指数选择最优特征,同时决定该特征的最优二值切分点。分类过程中,假设有K个类,样本点属于第k个类的概率为Pk,则概率分布的基尼指数定义为
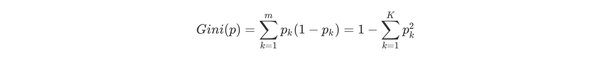
根据基尼指数定义,可以得到样本集合D的基尼指数,其中Ck表示数据集D中属于第k类的样本子集。
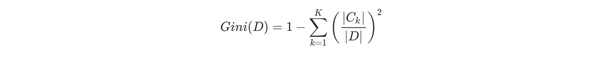
如果数据集D根据特征A在某一取值a上进行分割,得到D1,D2两部分后,那么在特征A下集合D的基尼系数如下所示。其中基尼系数Gini(D)表示集合D的不确定性,基尼系数Gini(D,A)表示A=a分割后集合D的不确定性。基尼指数越大,样本集合的不确定性越大。
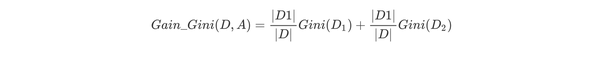
对于属性A,分别计算任意属性值将数据集划分为两部分之后的Gain_Gini,选取其中的最小值,作为属性A得到的最优二分方案。然后对于训练集S,计算所有属性的最优二分方案,选取其中的最小值,作为样本及S的最优二分方案。
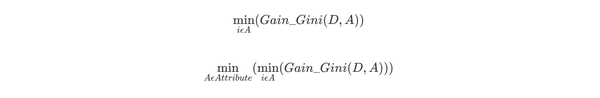
2.1实例详解
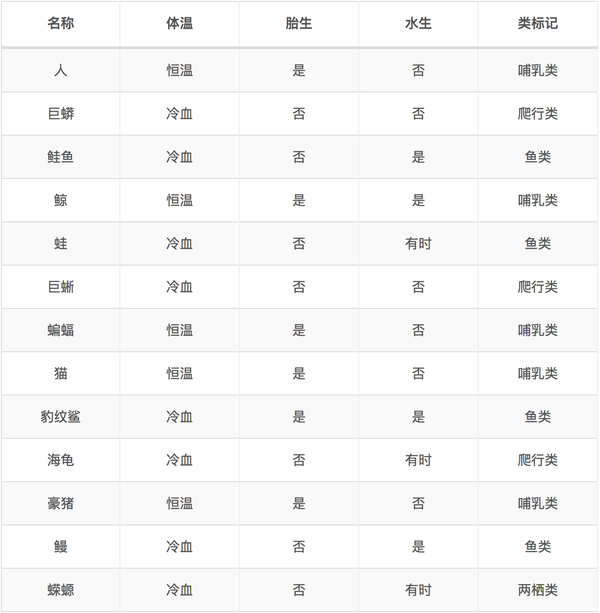
针对上述离散型数据,按照体温为恒温和非恒温进行划分。其中恒温时包括哺乳类5个、鸟类2个,非恒温时包括爬行类3个、鱼类3个、两栖类2个,如下所示我们计算D1,D2的基尼指数。
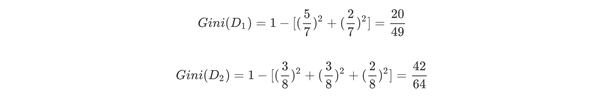
然后计算得到特征体温下数据集的Gini指数,最后我们选择Gain_Gini最小的特征和相应的划分。
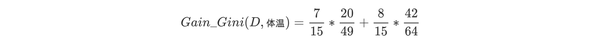
3.CART回归树
3.1算法详解
CART回归树预测回归连续型数据,假设X与Y分别是输入和输出变量,并且Y是连续变量。在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树。
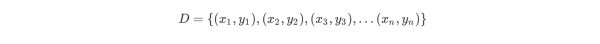
选择最优切分变量j与切分点s:遍历变量j,对规定的切分变量j扫描切分点s,选择使下式得到最小值时的(j,s)对。其中Rm是被划分的输入空间,cm是空间Rm对应的固定输出值。
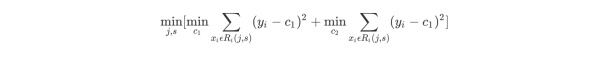
用选定的(j,s)对,划分区域并决定相应的输出值
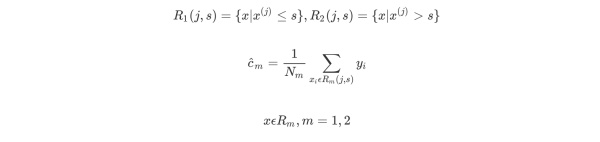
继续对两个子区域调用上述步骤,将输入空间划分为M个区域R1,R2,…,Rm,生成决策树。
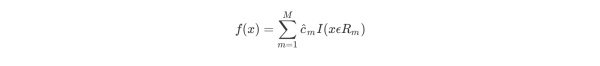
当输入空间划分确定时,可以用平方误差来表示回归树对于训练数据的预测方法,用平方误差最小的准则求解每个单元上的最优输出值。
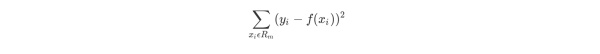
3.2实例详解

考虑如上所示的连续性变量,根据给定的数据点,考虑1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5切分点。
对各切分点依次求出R1,R2,c1,c2及m(s),例如当切分点s=1.5时,得到R1={1},R2={2,3,4,5,6,7,8,9,10},其中c1,c2,m(s)如下所示。
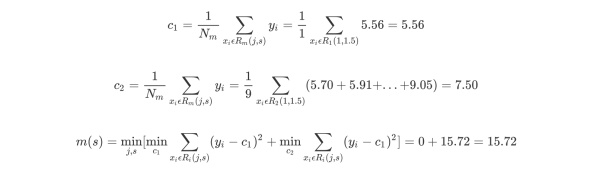
依次改变(j,s)对,可以得到s及m(s)的计算结果,如下表所示。

当x=6.5时,此时R1={1,2,3,4,5,6},R2={7,8,9,10},c1=6.24,c2=8.9。回归树T1(x)为
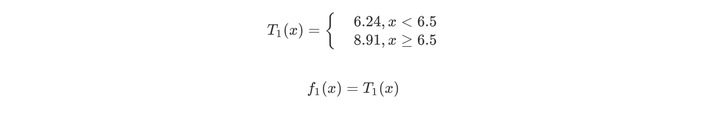
然后我们利用f1(x)拟合训练数据的残差,如下表所示

用f1(x)拟合训练数据得到平方误差
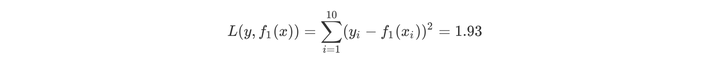
第二步求T2(x)与求T1(x)方法相同,只是拟合的数据是上表的残差。可以得到
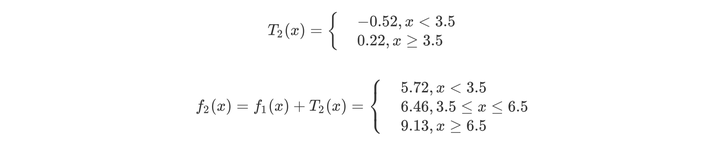
用f2(x)拟合训练数据的平方误差
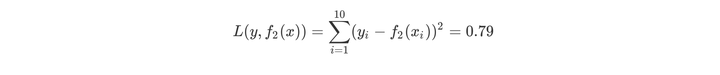
继续求得T3(x)、T4(x)、T5(x)、T6(x),如下所示

用f6(x)拟合训练数据的平方损失误差如下所示,假设此时已经满足误差要求,那么f(x)=f6(x)便是所求的回归树。
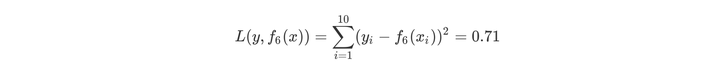
4.CART剪枝
代价复杂度剪枝算法:
我们将一颗充分生长的树称为T0 ,希望减少树的大小来防止过拟化。但同时去掉一些节点后预测的误差可能会增大,那么如何达到这两个变量之间的平衡则是问题的关键。因此我们用一个变量α 来平衡,定义损失函数如下
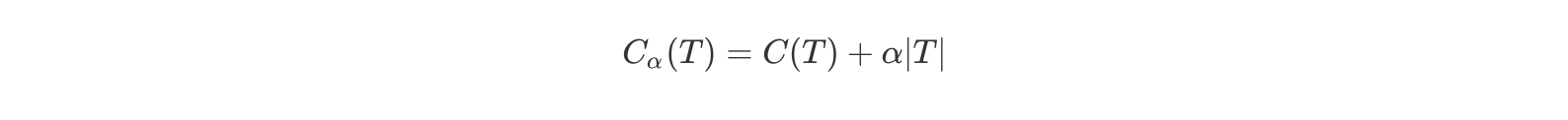
- T为任意子树,|T|为子树T的叶子节点个数。
- α是参数,权衡拟合程度与树的复杂度。
- C(T)为预测误差,可以是平方误差也可以是基尼指数,C(T)衡量训练数据的拟合程度。
那么我们如何找到这个合适的α来使拟合程度与复杂度之间达到最好的平衡呢?准确的方法就是将α从0取到正无穷,对于每一个固定的α,我们都可以找到使得Cα(T)最小的最优子树T(α)。
- 当α很小的时候,T0 是这样的最优子树.
- 当α很大的时候,单独一个根节点就是最优子树。
尽管α的取值无限多,但是T0的子树是有限个。Tn是最后剩下的根结点,子树生成是根据前一个子树Ti,剪掉某个内部节点后,生成Ti+1。然后对这样的子树序列分别用测试集进行交叉验证,找到最优的那个子树作为我们的决策树。子树序列如下
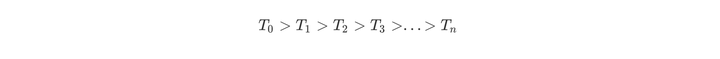
因此CART剪枝分为两部分,分别是生成子树序列和交叉验证。
5.sklearn
import pandas as pd
from sklearn import tree
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest) #返回预测的准确度accuracy score
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸'] import graphviz
dot_data = tree.export_graphviz(clf, out_file=".\Tree.dot"
,feature_names = feature_name
,class_names=["琴酒","雪莉","贝尔摩德"]
,filled=True
,rounded=True
)
import re
# 打开 dot_data.dot,修改 fontname="支持的中文字体"
f = open("./Tree.dot", "r+", encoding="utf-8")
open('./Tree_utf8.dot', 'w', encoding="utf-8").write(re.sub(r'fontname=helvetica', 'fontname="Microsoft YaHei"', f.read()))
f.close()
cmd:
dot -Tjpg Tree.dot -o tree.jpg
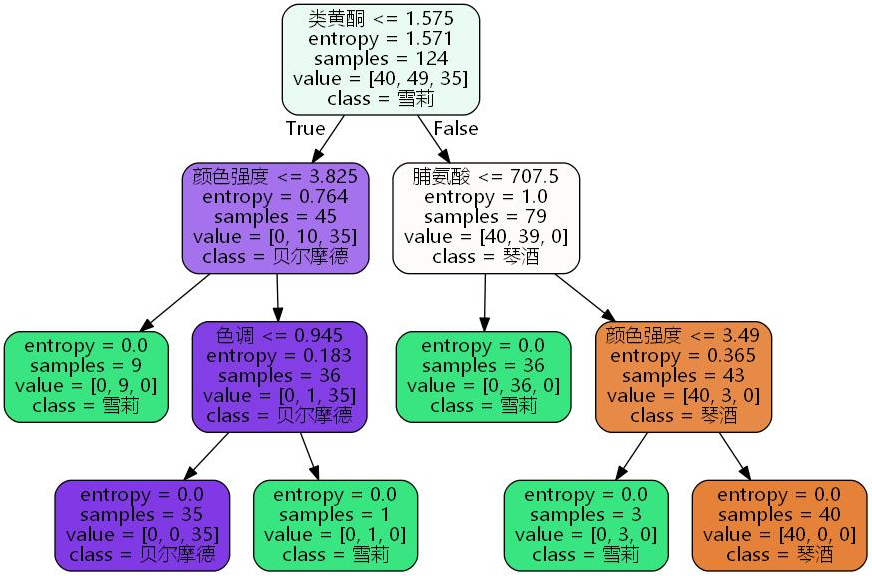
决策树--CART树详解的更多相关文章
- 数据结构图文解析之:AVL树详解及C++模板实现
0. 数据结构图文解析系列 数据结构系列文章 数据结构图文解析之:数组.单链表.双链表介绍及C++模板实现 数据结构图文解析之:栈的简介及C++模板实现 数据结构图文解析之:队列详解与C++模板实现 ...
- trie字典树详解及应用
原文链接 http://www.cnblogs.com/freewater/archive/2012/09/11/2680480.html Trie树详解及其应用 一.知识简介 ...
- Linux DTS(Device Tree Source)设备树详解之二(dts匹配及发挥作用的流程篇)【转】
转自:https://blog.csdn.net/radianceblau/article/details/74722395 版权声明:本文为博主原创文章,未经博主允许不得转载.如本文对您有帮助,欢迎 ...
- JavaScript---Dom树详解,节点查找方式(直接(id,class,tag),间接(父子,兄弟)),节点操作(增删改查,赋值节点,替换节点,),节点属性操作(增删改查),节点文本的操作(增删改查),事件
JavaScript---Dom树详解,节点查找方式(直接(id,class,tag),间接(父子,兄弟)),节点操作(增删改查,赋值节点,替换节点,),节点属性操作(增删改查),节点文本的操作(增删 ...
- 线段树详解 (原理,实现与应用)(转载自:http://blog.csdn.net/zearot/article/details/48299459)
原文地址:http://blog.csdn.net/zearot/article/details/48299459(如有侵权,请联系博主,立即删除.) 线段树详解 By 岩之痕 目录: 一:综述 ...
- Linux dts 设备树详解(二) 动手编写设备树dts
Linux dts 设备树详解(一) 基础知识 Linux dts 设备树详解(二) 动手编写设备树dts 文章目录 前言 硬件结构 设备树dts文件 前言 在简单了解概念之后,我们可以开始尝试写一个 ...
- Linux dts 设备树详解(一) 基础知识
Linux dts 设备树详解(一) 基础知识 Linux dts 设备树详解(二) 动手编写设备树dts 文章目录 1 前言 2 概念 2.1 什么是设备树 dts(device tree)? 2. ...
- AVL树详解
AVL树 参考了:http://www.cppblog.com/cxiaojia/archive/2012/08/20/187776.html 修改了其中的错误,代码实现并亲自验证过. 平衡二叉树(B ...
- trie树--详解
文章作者:yx_th000 文章来源:Cherish_yimi (http://www.cnblogs.com/cherish_yimi/) 转载请注明,谢谢合作.关键词:trie trie树 数据结 ...
随机推荐
- [CF544D]Destroying Roads_最短路_bfs
D. Destroying Roads 题目大意: In some country there are exactly n cities and m bidirectional roads conne ...
- MYsql 客户端下载地址
workbench: https://www.mysql.com/cn/products/workbench/
- Dijkstra(模板)
#define IOS ios_base::sync_with_stdio(0); cin.tie(0); #include <cstdio>//sprintf islower isupp ...
- PHP生成中文验证码并检测对错实例
PHP生成中文验证码并检测对错实例,中文验证码的例子还是比较少的,今天给大家分享一下,支持自定义中文.字体.背景色等 生成验证码,注意font字体路径要对,否则显示图片不存在 session_star ...
- python 基础(十八)--shutil模块
shutil模块 shutil.copyfileobj(src,dst):只拷贝文件内容,需要open文件:目标文件不存在时创建,存在时覆盖 shutil.copyfileobj(open('old. ...
- 查看linux服务器信息
1. vmstat 查看服务器内存,CPU等信息 一般是通过两个数字参数来完成的,第一个参数是采样时间间隔,单位是秒, 第二个参数是采样的次数 r: 表示运行队列,如果队列过大说明CPU很繁忙 ...
- JS基础_if练习一
<!DOCTYPE html> <html> <head> <meta charset="utf-8" /> <title&g ...
- 异常-Throwable的几个常见方法
package cn.itcast_04; import java.text.ParseException; import java.text.SimpleDateFormat; import jav ...
- shiro学习(五、springboot+shiro+mybatis+thymeleaf)
入门shiro(感觉成功了)首先感谢狂神,然后我就一本正经的复制代码了 项目结构 运行效果 数据库 <dependencies> <!-- thymeleaf-shiro整合包 -- ...
- java写webservice接口
有一个需求:要求根据设备mac和终端设备类型来查询设备库存状态. 接口协议是采用webservice协议,信息交互方式为xml格式信息 输入参数存放到XML各个节点下,并转为一个String,作为接口 ...
