pyecharts v1 版本 学习笔记 饼图,玫瑰图

饼图:

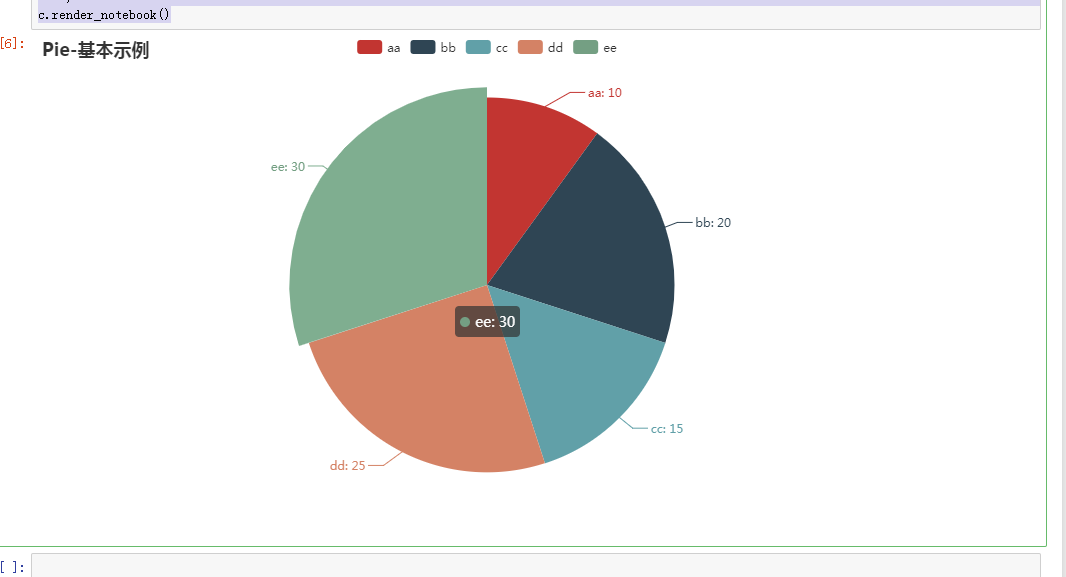
普通案例

from example.commons import Faker
from pyecharts import options as opts
from pyecharts.charts import Page, Pie
l1 = ['aa','bb','cc','dd','ee']
num =[10,20,15,25,30]
c = (
        Pie()
        .add("", [list(z) for z in zip(l1,num)])
        .set_global_opts(title_opts=opts.TitleOpts(title="Pie-基本示例"))
        .set_series_opts(label_opts=opts.LabelOpts(formatter="{b}: {c}"))
    )
c.render_notebook()

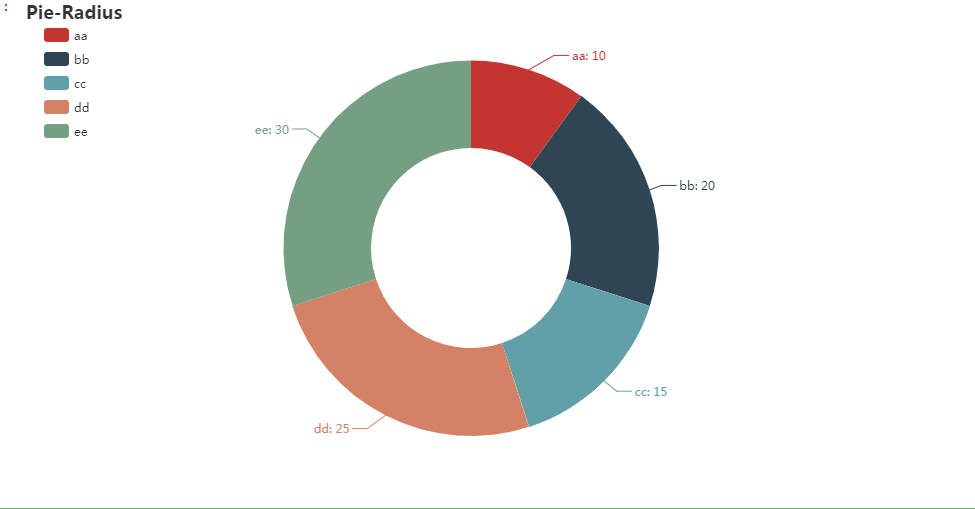
圆环图:

from example.commons import Faker
from pyecharts import options as opts
from pyecharts.charts import Page, Pie
l1 = ['aa','bb','cc','dd','ee']
num =[10,20,15,25,30]
c = (
        Pie()
        .add(
            "",
            [list(z) for z in zip(l1, num)],
            radius=["40%", "75%"],   # 圆环的粗细和大小
        )
        .set_global_opts(
            title_opts=opts.TitleOpts(title="Pie-Radius"),
            legend_opts=opts.LegendOpts(
                orient="vertical", pos_top="5%", pos_left="2%"  # 左面比例尺
            ),
        )
        .set_series_opts(label_opts=opts.LabelOpts(formatter="{b}: {c}"))
    )
c.render_notebook()

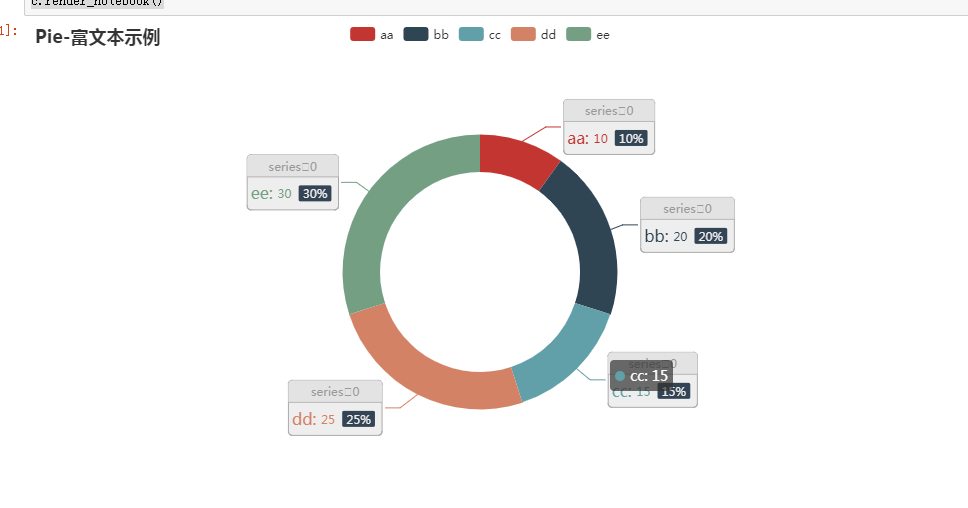
圆环显示百分比

from example.commons import Faker
from pyecharts import options as opts
from pyecharts.charts import Page, Pie
l1 = ['aa','bb','cc','dd','ee']
num =[10,20,15,25,30]
c = (
        Pie()
        .add(
            "",
            [list(z) for z in zip(l1, num)],
            radius=["40%", "55%"],
            label_opts=opts.LabelOpts(
                position="outside",
                formatter="{a|{a}}{abg|}\n{hr|}\n {b|{b}: }{c}  {per|{d}%}  ",
                background_color="#eee",
                border_color="#aaa",
                border_width=1,
                border_radius=4,
                rich={
                    "a": {"color": "#999", "lineHeight": 22, "align": "center"},
                    "abg": {
                        "backgroundColor": "#e3e3e3",
                        "width": "100%",
                        "align": "right",
                        "height": 22,
                        "borderRadius": [4, 4, 0, 0],
                    },
                    "hr": {
                        "borderColor": "#aaa",
                        "width": "100%",
                        "borderWidth": 0.5,
                        "height": 0,
                    },
                    "b": {"fontSize": 16, "lineHeight": 33},
                    "per": {
                        "color": "#eee",
                        "backgroundColor": "#334455",
                        "padding": [2, 4],
                        "borderRadius": 2,
                    },
                },
            ),
        )
        .set_global_opts(title_opts=opts.TitleOpts(title="Pie-富文本示例"))
    )
c.render_notebook()