后缀自动机----一种将字符串变成DAG的方法

后缀自动机 (suffix automaton, SAM) 是一个能解决许多字符串相关问题的有力的数据结构。(否则我们也不会用它)

举几个例子，以下的字符串问题都可以在线性时间内通过 SAM 解决

1.在另一个字符串中搜索一个字符串的所有出现位置。(诶？KMP好像能做)

2.计算给定的字符串中有多少个不同的子串。(诶？好像也能做)

3.统计一个子串所有不同子串的总长度 (额，线性复杂度？以前的知识好像就不行了)

4.字典序第k大/小子串(字典树好像可以做，但线性？不会！)

5.给定一个字符串 。找出字典序最小的循环移位。(这个我会！最小表示法！)

6.对于一个给定的文本串T ，有多组询问，每组询问给一个模式串S ，回答模式串S在字符串T中作为子串出现了多少次。(AC自动机！也可以)

7.给定一个字符串S 和一个特定的字符集，我们要找一个长度最短的没有在S中出现过的字符串。(以前的知识做不到我太菜了)

8.两个字符串的最长公共子串(线性？？！以前的知识做不到我太菜了)

9.多个字符串的最长公共子串(我不会！！)

这么多东西都可以线性时间内解决，厉害吧；

厉害的前提是你先要学会后缀自动机

接下来进入正题：

SAM是什么？

1.SAM 是一张有向无环图。结点被称作 状态 ，边被称作状态间的 转移 。

2.图存在一个源点root称作 初始状态 ，其它各结点均可从root出发到达。每个 转移 都标有一些字母。从一个结点出发的所有转移均 不同 。

3.存在一个或多个 终止状态 。如果我们从初始状态出发，最终转移到了一个终止状态，则路径上的所有转移连接起来一定是字符串S的一个后缀。

4.S的每个后缀均可用一条从到某个终止状态的路径构成。

5.在所有满足上述条件的自动机中，SAM 的结点数是最少的。

具体可以证明，SAM的点数最多是2*n-1,边数最多时3*n-4； （暂时为了方便理解并不证明，你只要露出"哇！这是上限吗"，"我靠，这SAM的复杂度也太***的强了"的表情就好了）;

SAM的性质：

SAM 最简单、也最重要的性质是，它包含关于字符串的所有子串的信息。任意从初始状态开始的路径，如果我们将转移路径上的标号写下来，都会形成S的一个子串 。反之每个S的子串对应从初始状态开始的某条路径。

为了更好的理解SAM（背模板，水经验），我们定义一些奇怪的东西；(不要一看到不认识的概念就跳过去，否则建图会看不懂的)

1.endpos等价类

考虑字符串S的任意非空子串t，我们记endpos(t)为在字符串S中t的所有结束位置.

让我们举个栗子：（假设对字符串中字符的编号从零开始）

对于S=“cbacbaba” endpos(ba)="2,5,7" endpos(a)="2,5,7" endpos(cba)="2,5";

我们发现，对于"ba"和"a"的endpos等价类的数值是完全相同的，那么这对与SAM来说是个好东西，我们可以将所有endpos相同的子串放到SAM的一个节点上，大大节省了空间与时间复杂度；

那么一个重要的结论出现了：SAM上的每个节点都代表一个endpos等价类；(比如刚才的栗子中，子串"ba","a"在SAM上用一个节点表示)

　我们发现一个不是引理的性质：对于一个子串S，不断的删除它开头的元素，那么它的endpos一定是在已有的旧元素基础上加入一些新元素(或者不加)，大致理解一下对于下面的引理很好理解

引理1:字符串S的两个非空子串x和y的endpos相同，当且仅当字符串x在S中的每次出现，都是以y后缀的形式存在的。(x<=y)  (很显然的对吧？)

   引理2：两个非空子串x,y, 他们的endpos的不可能存在交集 (很显然的对吧)

   引理3：考虑一个endpos等价类，将类中的所有子串按长度递减的顺序排序。每个子串是它前一个子串的后缀。

               换句话说，对于同一等价类的任一两子串，较短者为较长者的后缀，且该等价类中的子串长度恰好覆盖整个区间；

              粗略证明感性理解：对于一个endpos等价类中的最长子串x,和最短子串y，若y的开头加一个元素,使得新形成的字符串z是S的子串，那么如果z的长度<=x，则endpos(z)

一定=endpos(y)=endpos(x); 使用数学归纳法可以证明所有的y<=z<=x；z的endpos都与x,y相同；

2.后缀链接 link：

    考虑 SAM 中某个不是root的一个状态 。我们已经知道，状态v对应于具有相同endpos的等价类。我们如果定义x为这些字符串中最长的一个，则所有其它的字符串都是x的后缀。

　一个后缀链接link连接到对应于状态v的最短子串的所有后缀中长度最大的那个endpos等价类。　

引理1：所有后缀链接构成一棵根节点为root的树 (和造一颗随机树的原理相同：对于一个endpos等价类v，只会连到比v的最短子串小的endpos等价类)

    下面放两张图：对于字符串"abcbc",前者是表示边的转移状态，后者表示link的连接方式；

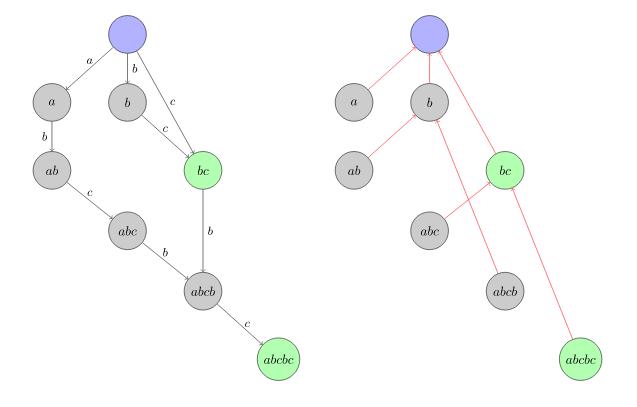
好了，定义暂时告一段落了；接下来就是构造环节了(代码)：(别人家的构造过程 (逃~)

！！极度建议结合之前的定义来阅读！！

代码实现就是：

class node{
	public:
	int ch[28];
	int link;
	int len;
}SAM[3000010];
int ans[3000010];
int last=0,size=1;
void SAM_build()
{
	SAM[0].len=0;
	n=strlen(s+1);
	SAM[0].link=-1;
	inc(u,1,n){
		int c=s[u]-'a';
		int cur=size++;
		ans[cur]=1;
		SAM[cur].len=SAM[last].len+1;
		int p=last;
		while(p!=-1&&!SAM[p].ch[c]){
			SAM[p].ch[c]=cur;
			p=SAM[p].link;
		}
		if(p==-1){
			SAM[cur].link=0;
		}
		else{
			int q=SAM[p].ch[c];
			if(SAM[q].len==SAM[p].len+1){
				SAM[cur].link=q;
			}
			else{
				int newq=size++;
				SAM[newq]=SAM[q];
				SAM[newq].len=SAM[p].len+1;
				while(p!=-1&&SAM[p].ch[c]==q){
					SAM[p].ch[c]=newq;
					p=SAM[p].link;
				}
				SAM[q].link=newq;
				SAM[cur].link=newq;
			}
		}
		last=cur;
	}
}