数据结构与算法-stack

栈的本质是一种线性表，特殊的一种线性表

基本概念

概念

栈是一种特殊的线性表

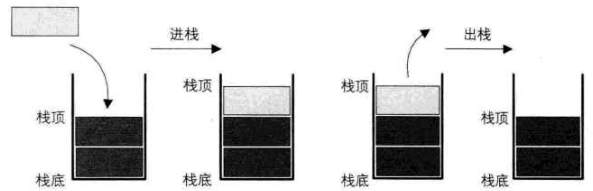
栈仅能在线性表的一端进行操作

• 栈顶(Top)：允许操作的一端
• 栈底(Bottom)：不允许操作的一端

stack是一种线性表，具有线性关系，即前驱后继关系，由于其比较特殊，增加和删除元素只能在栈顶进行

栈的插入操作叫做进栈，也称压栈，入栈

栈的删除操作叫做出栈，也称弹栈

常用操作

创建栈

销毁栈

清空栈

进栈

出栈

获取栈顶元素

获取栈的大小

#ifndef _MY_STACK_H_
#define _MY_STACK_H_

typedef void Stack;

Stack* Stack_Create();

void Stack_Destroy(Stack* stack);

void Stack_Clear(Stack* stack);

int Stack_Push(Stack* stack, void* item);

void* Stack_Pop(Stack* stack);

void* Stack_Top(Stack* stack);

int Stack_Size(Stack* stack);

#endif

栈的顺序存储设计与实现

基本概念

设计与实现

(*.h)

#ifndef __MY_SEQLIST_H__
#define __MY_SEQLIST_H__

typedef void SeqList;
typedef void SeqListNode;

SeqList* SeqStack_Create(int capacity);

void SeqStack _Destroy(SeqStack * list);

void SeqStack _Clear(SeqStack * list);

int SeqStack _Length(SeqStack * list);

int SeqStack _Capacity(SeqStack * list);

int SeqStack _Insert(SeqStack * list, SeqListNode* node, int pos);

SeqListNode* SeqList_Get(SeqList* list, int pos);

SeqListNode* SeqList_Delete(SeqList* list, int pos);

#endif

栈的顺序存储结构，就相当于链表的顺序存储结构，因此只要调用其功能完成即可

(*.c)

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#include "seqstack.h"
#include "seqlist.h"  //线性表的顺序存储头文件

SeqStack* SeqStack_Create(int capacity)
{
	return SeqList_Create(capacity);
}

void SeqStack_Destroy(SeqStack* stack)
{
	SeqList_Destroy(stack);
}

void SeqStack_Clear(SeqStack* stack)
{
	SeqList_Clear(stack);
}

//往栈中放元素，相当于向线性表中放元素
int SeqStack_Push(SeqStack* stack, void* item)
{
	return SeqList_Insert(stack, item, SeqList_Length(stack));
}

//从栈中弹出元素，相当于从线性表中删除元素
void* SeqStack_Pop(SeqStack* stack)
{
	return SeqList_Delete(stack, SeqList_Length(stack) - 1);
}

void* SeqStack_Top(SeqStack* stack)
{
	return SeqList_Get(stack, SeqList_Length(stack) - 1);
}

int SeqStack_Size(SeqStack* stack)
{
	return SeqList_Length(stack);
}

int SeqStack_Capacity(SeqStack* stack)
{
	return SeqList_Capacity(stack);
}

(test)

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#include "seqstack.h"

void main()
{
	int a[20], i = 0;
	int *pTmp = NULL;
	SeqStack* stack = NULL;

	stack = SeqStack_Create(20);

	for (i=0; i<10; i++)
	{
		a[i] = i+1;
		//SeqStack_Push(stack, &a[i]);
		SeqStack_Push(stack, a+i);
	}

	pTmp = (int *)SeqStack_Top(stack);
	printf("top:%d \n", *pTmp);

	printf("capacity:%d \n", SeqStack_Capacity(stack));

	printf("size:%d \n", SeqStack_Size(stack));

	//元素出栈
	while (SeqStack_Size(stack) > 0)
	{
		printf("pop:%d \n", *((int *)SeqStack_Pop(stack)));
	}

	SeqStack_Destroy(stack);

	system("pause");
}

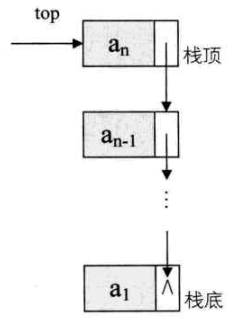
栈的链式存储设计与实现

基本概念

通常对于链栈来说，是不需要头结点的

设计与实现

(*.h)

#ifndef __MY_LINKSTACK_H_
#define __MY_LINKSTACK_H_

typedef void LinkStack;

LinkStack* LinkStack_Create();

void LinkStack_Destroy(LinkStack* stack);

void LinkStack_Clear(LinkStack* stack);

int LinkStack_Push(LinkStack* stack, void* item);

void* LinkStack_Pop(LinkStack* stack);

void* LinkStack_Top(LinkStack* stack);

int LinkStack_Size(LinkStack* stack);

#endif

栈的链式存储结构，就相当于链表的链式存储结构，因此只要调用其功能完成即可

(*.c)

#include <stdlib.h>
#include <stdio.h>
#include <string.h>

#include "linkstack.h"
#include "linklist.h"

typedef struct _tag_LinkStackNode
{
	LinkListNode node;
	void *item;
}TLinkStackNode;

LinkStack* LinkStack_Create()
{
	//创建一个栈，通过线性表去模拟
	return LinkList_Create();
}

void LinkStack_Destroy(LinkStack* stack)
{
	LinkStack_Clear(stack); //注意 destory的时候，需要把栈中的所有元素都清空
	LinkList_Destroy(stack);
}

void LinkStack_Clear(LinkStack* stack)
{
	//LinkList_Clear(stack);
	while (LinkStack_Size(stack) > 0)
	{
		LinkStack_Pop(stack); //在这个函数里面有内存释放函数
	}
	return;
}

//向栈中放元素，相当于向线性表中插入一个元素
int LinkStack_Push(LinkStack* stack, void* item)
{
	int ret = 0;
	//需要item数据，转换成 linklist的业务节点
	TLinkStackNode *pTe = (TLinkStackNode *)malloc(sizeof(TLinkStackNode));
	if (pTe == NULL)
	{
		return -1;
	}
	pTe->item = item;

	//头插法，向线性表中插入元素，插入元素的时候，需要构造业务节点
	ret = LinkList_Insert(stack, (LinkListNode *)(&pTe->node), 0);
	if (ret != 0)
	{
		free(pTe);
	}
	return ret;
}

void* LinkStack_Pop(LinkStack* stack)
{
	void *myItem = NULL;
	TLinkStackNode *pTmp = NULL;
	pTmp = (TLinkStackNode *)LinkList_Delete(stack, 0);
	if (pTmp == NULL)
	{
		return NULL;
	}
	myItem = pTmp->item;

	//注意向线性表中插入元素的时，打造节点，分配内存；
	//弹出元素时，需要释放节点内存
	if (pTmp != NULL)
	{
		free(pTmp);
	}
	return myItem;
}

void* LinkStack_Top(LinkStack* stack)
{
	void *myItem = NULL;
	TLinkStackNode *pTmp = NULL;
	pTmp = (TLinkStackNode *)LinkList_Get(stack, 0);
	if (pTmp == NULL)
	{
		return NULL;
	}
	myItem = pTmp->item;
	return myItem;
}

int LinkStack_Size(LinkStack* stack)
{
	return LinkList_Length(stack);
}

(test)

#include <stdlib.h>
#include <stdio.h>
#include <string.h>

#include "linkstack.h"

void main()
{
	int a[10], i;
	LinkStack *stack = NULL;

	stack = LinkStack_Create();

	for (i = 0; i < 10; i++)
	{
		a[i] = i + 1;
		LinkStack_Push(stack, &a[i]);
	}
	printf("top: %d \n", *((int *)LinkStack_Top(stack)));
	printf("size: %d \n", LinkStack_Size(stack));

	//删除栈中所有元素
	while (LinkStack_Size(stack) > 0)
	{
		printf("linkstack pop: %d \n", *((int*)LinkStack_Pop(stack)));
	}
	LinkStack_Destroy(stack);

	system("pause");
}

栈的应用

就近匹配

几乎所有的编译器都具有检测括号是否匹配的能力

如何实现编译器中的符号成对检测？

#include <stdio.h> int main() { int a[4][4]; int (*p)[4]; p = a[0]; return 0;

算法思路

• 从第一个字符开始扫描
• 当遇见普通字符时忽略，当遇见左符号时压入栈中
• 当遇见右符号时从栈中弹出栈顶符号，并进行匹配
• 匹配成功：继续读入下一个字符
• 匹配失败：立即停止，并报错

结束：

• 成功: 所有字符扫描完毕，且栈为空
• 失败：匹配失败或所有字符扫描完毕但栈非空

当需要检测成对出现但又互不相邻的事物时

可以使用栈“后进先出”的特性

栈非常适合于需要“就近匹配”的场合

#include <stdio.h>
#include <stdlib.h>

#include "linkstack.h"

int isLeft(char c)
{
	int ret = 0;
	switch (c)
	{
	case '<':
	case '(':
	case '[':
	case '{':
	case '\'':
	case '\"':
		ret = 1;
		break;
	default:
		ret = 0;
		break;
	}
	return ret;
}

int isRight(char c)
{
	int ret = 0;
	switch (c)
	{
	case '>':
	case ')':
	case ']':
	case '}':
	case '\'':
	case '\"':
		ret = 1;
		break;
	default:
		ret = 0;
		break;
	}
	return ret;
}

int match(char left, char right)
{
	int ret = 0;
	switch (left)
	{
	case '<':
		ret = (right == '>');
		break;
	case '(':
		ret = (right == ')');
		break;
	case '[':
		ret = (right == ']');
		break;
	case '{':
		ret = (right == '}');
		break;
	case '\'':
		ret = (right == '\'');
		break;
	case '\"':
		ret = (right == '\"');
		break;
	default:
		ret = 0;
		break;
	}
	return ret;
}

int scanner(const char* code)
{
	LinkStack*	stack = LinkStack_Create();
	int			ret = 0;
	int			i = 0;

	while (code[i] != '\0')
	{
		if (isLeft(code[i]))
		{
			LinkStack_Push(stack, (void*)(code + i)); //&code[i]
		}

		if (isRight(code[i]))
		{
			char* c = (char*)LinkStack_Pop(stack);
			if ((c == NULL) || !match(*c, code[i]))
			{
				printf("%c does not match!\n", code[i]);
				ret = 0;
				break;
			}
		}
		i++;
	}

	if ((LinkStack_Size(stack) == 0) && (code[i] == '\0'))
	{
		printf("Succeed!\n");
		ret = 1;
	}
	else
	{
		printf("fail!\n");
		ret = 0;
	}

	LinkStack_Destroy(stack);

	return ret;
}

void main()
{
	const char* code = "#include <stdio.h> int main() { int a[4][4]; int (*p)[4]; p = a[0]; return 0; ";
	scanner(code);
	system("pause");
	return;
}

中缀与后缀

计算机的本质工作就是做数学运算

那么计算机是如何处理数学表达式的?

波兰科学家在20世纪50年代提出了一种将运算符放在数字后面的后缀表达式对应的，我们习惯的数学表达式叫做中缀表达式

5 + 4=> 5 4 +

1 + 2 * 3 => 1 2 3 * +

8 + ( 3 – 1 ) * 5 => 8 3 1 – 5 * +

中缀表达式符合人类的阅读和思维习惯

后缀表达式符合计算机的运算习惯

中缀转后缀算法：

• 遍历中缀表达式中的数字和符号
• 对于数字：直接输出
• 对于符号：
  • 左括号：进栈
  • 运算符号：与栈顶符号进行优先级比较
    • 若栈顶符号优先级低：此符合进栈 （默认栈顶若是左括号，左括号优先级最低）
    • 若栈顶符号优先级不低：将栈顶符号弹出并输出，之后进栈
    • 右括号：将栈顶符号弹出并输出，直到匹配左括号
• 遍历结束：将栈中的所有符号弹出并输出
  
  
  
  中缀转后缀

#include <stdio.h>
#include <stdlib.h>

#include "linkstack.h"

int isNumber(char c)
{
	return ('0' <= c) && (c <= '9');
}

int isOperator(char c)
{
	return (c == '+') || (c == '-') || (c == '*') || (c == '/');
}

int isLeft(char c)
{
	return (c == '(');
}

int isRight(char c)
{
	return (c == ')');
}

int priority(char c)
{
	int ret = 0;
	if ((c == '+') || (c == '-'))
	{
		ret = 1;
	}
	if ((c == '*') || (c == '/'))
	{
		ret = 2;
	}
	return ret;
}

void output(char c)
{
	if (c != '\0')
	{
		printf("%c", c);
	}
}

void transform(const char* exp)
{
	int			i = 0;
	LinkStack*	stack = LinkStack_Create();

	while (exp[i] != '\0')
	{
		if (isNumber(exp[i]))
		{
			output(exp[i]);
		}
		else if (isOperator(exp[i]))
		{
			while (priority(exp[i]) <= priority((char)(int)LinkStack_Top(stack)))
			{
				output((char)(int)LinkStack_Pop(stack));
			}

			LinkStack_Push(stack, (void*)(int)exp[i]);
		}
		else if (isLeft(exp[i]))
		{
			LinkStack_Push(stack, (void*)(int)exp[i]);
		}
		else if (isRight(exp[i]))
		{
			//char c = '\0';
			while (!isLeft((char)(int)LinkStack_Top(stack)))
			{
				output((char)(int)LinkStack_Pop(stack));
			}

			LinkStack_Pop(stack);
		}
		else
		{
			printf("Invalid expression!");
			break;
		}
		i++;
	}

	while ((LinkStack_Size(stack) > 0) && (exp[i] == '\0'))
	{
		output((char)(int)LinkStack_Pop(stack));
	}

	LinkStack_Destroy(stack);
}

int main()
{
	transform("8+(3-1)*5");
	printf("\n");
	system("pause");
	return 0;
}

后缀表达式计算：

• 遍历后缀表达式中的数字和符号
• 对于数字：进栈
• 对于符号：
  • 从栈中弹出右操作数
  • 从栈中弹出左操作数
  • 根据符号进行运算
  • 将运算结果压入栈中
• 遍历结束：栈中的唯一数字为计算结果
  
  

#include <stdio.h>
#include <stdlib.h>

#include "linkstack.h"

int isNumber(char c)
{
	return ('0' <= c) && (c <= '9');
}

int isOperator(char c)
{
	return (c == '+') || (c == '-') || (c == '*') || (c == '/');
}

int value(char c)
{
	return (c - '0');
}

int express(int left, int right, char op)
{
	int ret = 0;
	switch (op)
	{
	case '+':
		ret = left + right;
		break;
	case '-':
		ret = left - right;
		break;
	case '*':
		ret = left * right;
		break;
	case '/':
		ret = left / right;
		break;
	default:
		break;
	}
	return ret;
}

int compute(const char* exp)
{
	LinkStack*	stack = LinkStack_Create();
	int			ret = 0;
	int			i = 0;

	while (exp[i] != '\0')
	{
		if (isNumber(exp[i]))
		{
			LinkStack_Push(stack, (void*)value(exp[i]));
		}
		else if (isOperator(exp[i]))
		{
			int right = (int)LinkStack_Pop(stack);
			int left = (int)LinkStack_Pop(stack);
			int result = express(left, right, exp[i]);

			LinkStack_Push(stack, (void*)result);
		}
		else
		{
			printf("Invalid expression!");
			break;
		}
		i++;
	}

	if ((LinkStack_Size(stack) == 1) && (exp[i] == '\0'))
	{
		ret = (int)LinkStack_Pop(stack);
	}
	else
	{
		printf("Invalid expression!");
	}

	LinkStack_Destroy(stack);

	return ret;
}

int main()
{
	printf("8 + (3 - 1) * 5  = %d\n", compute("831-5*+"));
	system("pause");
	return 0;
}