linux网络编程之system v消息队列(一)

经过上次对于进程通讯的一些理论的认识之后，接下来会通过实验来进一步加深对进程通讯的认识，话不多说，进入正题：

其实还可以通过管道，但是，管道是基于字节流的，所以通常会将它称为流管道，数据与数据之间是没有边界的；而消息队列是基于消息的，数据与数据之间是有边界的，这是消息队列跟管道有区别的地方，另外一个差别就是在于接收：消息队列在接收是不一定按先入先出，而管道一定是按照先入先出的原则来进行接收的。

关于这些，可以通过命令来查看其值，如下：

上次提到过，System_V IPC对象有三种，如下：

这些IPC对象都是随内核持续的，也就是说当访问这些对象的最后一个进程结束时候，内核也不会自动删除这些对象，直到我们显示删除这些对象才能够从内核中删除掉，所以说内核必须为每个IPC对象维护一个数据结构，其形式如下：

下面来看下消息队列的具体结构是怎么样的：

这里先学前两个函数:

下面则用代码来学习一下该函数：

下面编译运行一下：

从图中可以看出创建失败了，这是为什么呢？这时可以查看其帮助：

实际上msgget函数类似于open函数一样，如果在open一个文件时没有指定O_CREATE选项，则不能够创建一个文件，同样的：

如果创建失败，则会返回：

所以修改代码如下：

再次编译运行：

那创建成功的消息队列怎么查看呢？可以通过如下命令：

如果再次运行呢？

发现又成功了，那再查看一下消息队列：

修改代码如下：

其错误代码是：

可见每运行一次则就创建成功一个新的消息队列，而且key都是为0，这意味着两个进程就无法共享同一个消息队列了，但是同一个进程还是可以共享的，其实也可以有一个办法达到两个不同进程进行共享，就是将消息队列id保存到文件当中，另一个进程读取消息队列id来获得消息队列，这样也能实现共享，只是麻烦一些，这里就不多赘述了。另外如果key值为IPC_PRIVATE，那么没有IPC_CREATE选项也一样会创建成功，如下：

编译运行：

另外一旦一个消息队列创建成功之后，如果要打开一个消息队列，这时候就不用指定IPC_CREATE了，而且参数值可以直接填0:

接下来删除一些已经创建的消息队列，有两种方式：

那如果像这剩下key全为0的，用这种方式还能起作用么，咱们来试一下：

下面来说一个权限的问题：

编译运行：

下面来以600更高的权限来打开刚才创建低权限的消息队列：

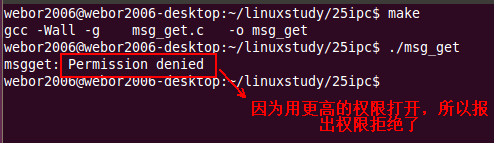
那有木有一种办法，在打开消息队列时，就以原创建的权限打开，当然有，也就是打开时不指定权限既可，如下：

上面演示了各种msgget创建用法，下面来用图来总结一下各个情况：

接下来学习一下消息队列的按制函数，如下：

上面已经用命令知道怎么删除已经创建的消息队列了，下面采用代码来实现消息队列的删除：

接下来来获取消息队列的信息，这时需要就需要关注第三个参数了，man查看一下：

而其中ipc_perm结构体内容如下：

下面来实验一下：

编译运行：

下面来更改一下消息队列的状态，将权限666改为600，具体做法如下：

【说明】:上图中用到了sscanf函数来将一个指定的字符串赋值给变量，对于scanf函数大家应该都不陌生，它是从标准输入中赋值变量，而sscanf是将指定的字符串按指定的格式赋给变量，两者的唯一区别就是数据的来源变了，很容易理解。

编译运行：

好了，今天的内容有些多，需好好消化，下节消息队列继续~~