【做题】CF196E. Opening Portals 排除无用边&最小生成树

题意：给出一个有\(n\)个结点，\(m\)条边的连通无向图，边有边权，等于经过这条边所需的时间。有\(k\)个点设有传送门。一开始，所有传送门关闭。你从\(1\)号点出发，每当你到达一个有传送门的点，那个传送门就会永久开启。你可以从一个开启的传送门花费\(0\)时间到达另一个开启的传送门。求开启所有传送门所需的最小时间。

\(n,m \leq 10^5\)

首先，简化一下题目。当到达第一个传送门点后，因为已经过传送门可以互相传送，所以剩下的时间就是所有传送门点两两之间连权值等于最短路的边建成的完全图的最小生成树。因此答案就是那个最小生成树，再加上\(1\)号点到最近的传送门的距离。

因此，我们得到了一个\(O(n^2 \log n)\)的算法。

接下来，问题就变成了如何快速求最小生成树。不难想到，如果传送门点\(u\)到\(v\)的最短路上有其他传送门点，那么\((u,v)\)一定不在MST上。遗憾的是，单单这么剪枝是没有用的，边数还是会被下图所示的菊花卡成\(O(n^2)\)。

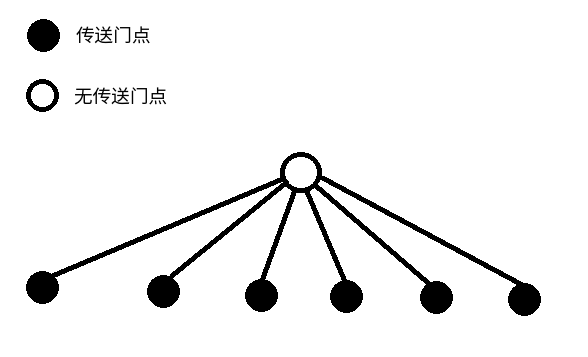
但是，这个失败的尝试启示我们要剪去一些不可能在最小生成树上的边。考虑kruskal的过程，一条边只要在一个其他边都“小于”它的环上（指边权小于或边权等于但枚举顺序靠前），就一定不在最小生成树上。

我们难以直接判断这个条件，但是，对于一条最短路径，如果它上面的每一条边两端最近的传送门点都不是这条路径的两个端点，就可以排除了。因此，我们构建一张新图\(G'\)，对于原图上每一条边\((u,v)\)，设与\(u\)最近的任意一个传送门点为\(nex_u\)，与\(v\)最近的是\(nex_v\)，那么，在新图上建一条\((nex_u,nex_v)\)的边，边权是原边权加上\(dis(nex_u,u) + dis(nex_v,v)\)。这相当于考虑所有边所在的最短路，并且，所有没有被考虑到的最短路一定是可以删去的。这样，我们就把边数剪到了\(O(n)\)级别。

时间复杂度\(O(n \log n)\)。

#include <bits/stdc++.h>
using namespace std;

#define gc() getchar()
template <typename tp>
inline void read(tp& x) {
  char tmp; bool key = 0;
  x = 0;
  for (tmp = gc() ; !(tmp >= '0' && tmp <= '9') ; tmp = gc())
    key = (tmp == '-');
  for ( ; tmp >= '0' && tmp <= '9' ; tmp = gc())
    x = (x << 3) + (x << 1) + tmp - '0';
  if (key) x = -x;
}
// begin here
typedef long long ll;
const int N = 100010;
const ll INF = 1ll << 60;
struct edge {
  int la,b,v;
} con[N << 1];
int tot,fir[N];
void add(int from,int to,int val) {
  con[++tot] = (edge) {fir[from],to,val};
  fir[from] = tot;
}
int n,m,vis[N],num,nex[N],uni[N];
ll dis[N],ans = INF;
struct data {
  int a,b;
  ll v;
  bool operator < (const data& x) const {
    return v < x.v;
  }
} dat[N];
typedef pair<ll,int> pii;
struct cmp {
  bool operator () (const pii& a,const pii& b) {
    return a > b;
  }
};
priority_queue<pii,vector<pii>,cmp> q;
vector<int> st;
void dijkstra() {
  while (!q.empty()) q.pop();
  memset(dis,0x3f,sizeof dis);
  memset(vis,0,sizeof vis);
  for (int i = 0 ; i < (int)st.size() ; ++ i) {
    dis[st[i]] = 0;
    nex[st[i]] = st[i];
    q.push(pii(dis[st[i]],st[i]));
  }
  for (int pos ; !q.empty() ; ) {
    pos = q.top().second;
    q.pop();
    if (vis[pos]) continue;
    vis[pos] = 1;
    for (int i = fir[pos] ; i ; i = con[i].la) {
      if (dis[con[i].b] > dis[pos] + con[i].v) {
        dis[con[i].b] = dis[pos] + con[i].v;
        nex[con[i].b] = nex[pos];
        q.push(pii(dis[con[i].b],con[i].b));
      }
    }
  }
}
int getfa(int pos) {
  return pos == uni[pos] ? pos : uni[pos] = getfa(uni[pos]);
}
int main() {
  int x,y,z;
  read(n), read(m);
  for (int i = 1 ; i <= m ; ++ i) {
    read(x), read(y), read(z);
    dat[i] = (data) {x,y,z};
    add(x,y,z);
    add(y,x,z);
  }
  st.clear();
  st.push_back(1);
  dijkstra();
  st.clear();
  read(num);
  for (int i = 1 ; i <= num ; ++ i) {
    read(x);
    ans = min(ans,dis[x]);
    st.push_back(x);
  }
  dijkstra();
  for (int i = 1 ; i <= n ; ++ i)
    uni[i] = i;
  for (int i = 1 ; i <= m ; ++ i) {
    dat[i].v += dis[dat[i].a] + dis[dat[i].b];
    dat[i].a = nex[dat[i].a];
    dat[i].b = nex[dat[i].b];
  }
  sort(dat+1,dat+m+1);
  for (int i = 1 ; i <= m ; ++ i) {
    x = dat[i].a, y = dat[i].b;
    x = getfa(x), y = getfa(y);
    if (x == y) continue;
    uni[x] = y;
    ans += dat[i].v;
  }
  cout << ans << endl;
  return 0;
}

小结：这类知识点简单的题目还是很有思维难度的。这一点，还要弥补。