hdu 1757 和1005差不多 (矩阵快速幂)

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1

求f（n）%MOD

Sample Input
10 9999 //n mod
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

Sample Output
45
104

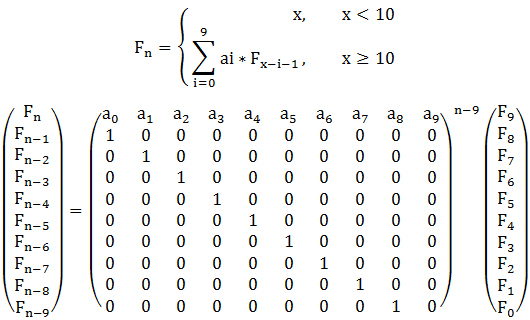
 # include <iostream>
 # include <cstdio>
 # include <cstring>
 # include <algorithm>
 # include <cmath>
 using namespace std ;
 
 int MOD ;
 
 struct Matrix
 {
     int mat[][];
 };
 
 Matrix mul(Matrix a,Matrix b) //矩阵乘法
 {
     Matrix c;
     for(int i=;i<;i++)
         for(int j=;j<;j++)
         {
             c.mat[i][j]=;
             for(int k=;k<;k++)
             {
                 c.mat[i][j]=(c.mat[i][j] + a.mat[i][k]*b.mat[k][j])%MOD;
             }
         }
     return c;
 }
 Matrix pow_M(Matrix a,int k)  //矩阵快速幂
 {
     Matrix ans;
     memset(ans.mat,,sizeof(ans.mat));
     for (int i=;i<;i++)
         ans.mat[i][i]=;
     Matrix temp=a;
     while(k)
     {
         if(k&)ans=mul(ans,temp);
         temp=mul(temp,temp);
         k>>=;
     }
     return ans;
 }
 
 int main ()
 {
     //freopen("in.txt","r",stdin) ;
     int n  ;
     while(cin>>n>>MOD)
     {
         Matrix t ;
         int i , j ;
         for (i =  ; i <  ; i++)
             cin>>t.mat[][i] ;
         if (n < )
         {
             cout<<n<<endl ;
             continue ;
         }
         for (i =  ; i <  ; i++)
             for (j =  ; j <  ; j++)
         {
             if (i ==(j+))
                 t.mat[i][j] =  ;
             else
                 t.mat[i][j] =  ;
         }
         Matrix ans = pow_M(t,n-) ;
         int sum =  ;
         for (i =  ; i <  ; i++)
         {
             sum = (sum + ans.mat[][i]*(-i))%MOD ;
         }
         cout<<sum<<endl ;
 
     }
 
     return  ;
 }