LOJ10013曲线

题目描述

明明做作业的时候遇到了n  个二次函数s_i(x)=ax^2+bx+c ，他突发奇想设计了一个新的函数 f(x)=max{s_i(x)},i=1,2,...,n。

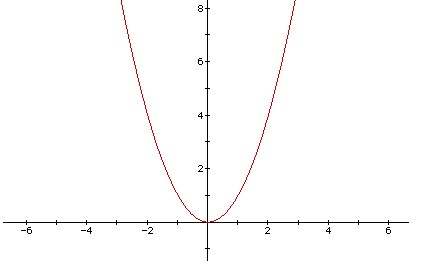
明明现在想求这个函数在 [0,1000] 的最小值，要求精确到小数点后四位，四舍五入。

输入格式

输入包含 t 组数据，每组第一行一个整数n ；

接下来 n 行，每行 3 个整数 a,b,c  ，用来表示每个二次函数的 3 个系数。注意：二次函数有可能退化成一次。

输出格式

每组数据输出一行，表示新函数 f(x) 的在区间 [0,1000] 上的最小值。精确到小数点后四位，四舍五入。

样例

样例输入

2
1
2 0 0
2
2 0 0
2 -4 2

样例输出

0.0000
0.5000

数据范围与提示

对于 50% 的数据，1<=n<=100；

对于 100% 的数据，1<=t<=10,1<=n<=1e5 ,1<=a<=100 ,1<=|b|<=5e3 ,0<=|c|<=5e3 。

___________________________________________

这个题目用到分治中的一种特殊形式，三分。

首先，题目的真正难点在于能够看出：n个函数的最大值构成的新函数仍然是一个开口向上的波谷。

然后就是三分了。三分用来求波谷的最小值（或波峰的最大值）

以求波谷的最小值为例：

求区间[l,r]上的最小值，首先把区间长度等分成三分，分割点为ll和rr

sf=(r-l)/3

ll=l+sf,rr=r-sf;

这样区间就变成了[l,ll,rr,r]四点分成的三份。

然后求ll和rr点对应的函数值，由于是波谷，那么谷底所在点可能有三个可能：

1、在[ll,rr]区间内，由于是波谷，开口向上，那么f[l]>f[ll],f[rr]<f[r]，那么可以去掉[l,ll]和[rr,r]两个区间。

2、在[l,ll]区间内，由于是波谷，开口向上，那么f[ll]<f[rr]<f[r]，那么可以去掉[ll,rr]和[rr,r]两个区间。

3、在[rr,r]区间内，由于是波谷，开口向上，那么f[l]>f[ll]>f[rr]，那么可以去掉[l,ll]和[ll,rr]两个区间。。

那么综合上面三种情况，如果f[ll]>f[rr]，那么谷底可能在中间区[ll,rr]或右侧区[rr,r]，那么左侧[l,rr]去掉;如果f[ll]<f[rr]，那么谷底可能在中间区[ll,rr]或左侧区[l,ll]，那么右侧[rr,r]去掉.

___________________________________________

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int maxn=1e5+10;
 4 int a[maxn],b[maxn],c[maxn];
 5 int t,n;
 6 double work(double x)
 7 {
 8     double rt=-1e9;
 9     for(int i=1;i<=n;++i)
10         rt=max(rt,a[i]*x*x+b[i]*x+c[i]);
11     return rt;
12 }
13 int main()
14 {
15     scanf("%d",&t);
16     while(t--)
17     {
18         scanf("%d",&n);
19         for(int i=1;i<=n;++i)
20             scanf("%d%d%d",a+i,b+i,c+i);
21         double l=0,r=1000,ll,rr;
22         while(l+1e-10<r)
23         {
24             double sf=(r-l)/3;
25             ll=l+sf;rr=r-sf;
26             if(work(ll)<work(rr))r=rr;
27             else l=ll;
28         }
29         printf("%.4lf\n",work((l+r)/2));
30     }
31     return 0;
32 }