LCA树上倍增求法

1.LCA

LCA就是最近公共祖先（Least common ancestor），x,y的LCA记为z=LCA(x,y)，满足z是x，y的公共祖先中深度最大的那一个（即离他们最近的那一个）qwq

2.问题引入

看LCA之前最好学一下并查集，因为这两个东西有点相似，不同之处在于并查集一旦进行了路径压缩，便只能求出两个点之间是否存在关系，无法精确判断谁是谁的祖先以及两者的深度最大的公共祖先（只能判断有没有公共祖先）。

但LCA就不一样了，他可以实现并查集的操作，还可以查询两者的最近祖先，emm，关于这一点的应用嘛，就是比如说求树上最短路的问题，LCA会方便很多

3.LCA倍增算法本法

LCA的雏形就是单纯地考虑x，y同时向自己的爸爸跳，直到相遇，但如果是两条链连在树根上，x,y又分别是两个叶子结点的话。。。。会很慢很慢

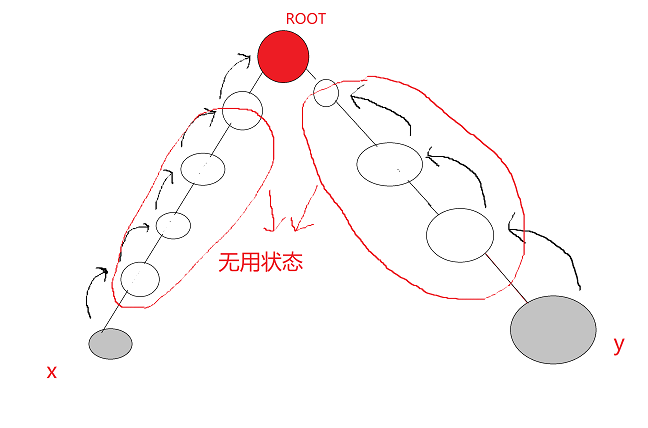
那么问题来了：怎么优化？？？

不知道大家有没有想过我们为什么要使用树形结构？单纯是为了好看嘛？显然不是的。个人认为树形结构的优点之一在于：其特有的结构在搜索时可以极大地缩减深度，避免了一些不必要的试探

从而节约了时间。那么，当一棵树退化为一条链的时候，这个优点便不那么明显了，甚至会退化为普通的搜索算法。问题的关键在于我们在搜索时是一步一步地向前试探，但如果存在x，y的深度相差很

大的情况，那么，两个结点回溯到深度都为dep的祖先之前的试探其实都是无效的，这也是普通算法低效的原因所在。那么我们可不可以一次向上多跳几步呢？如果可以，我们应该怎么表示这种状态呢？

这里介绍一种倍增的思想，即每次向上跳2^k步，其中k为大于等于0的整数。不妨设x跳了2^k步后到达的结点为z，如果dep[z]>=dep[y],那么证明这一步试探也是无效的，但是否说明这个状态没有用呢？

其实不然。类似于快速幂的算法，x向上跳2^k步，其实等价于x先向上跳2^(k-1)步再向上跳2^(k-1)步，这也是我们为什么选择向上跳2的整数次幂步的原因，这是一种极其高效的方法，而且便于处理。

那么，我怎么知道向上跳2^k步后到达了哪个结点呢？这时候就需要预处理，不妨设f[x][k]表示x结点向上跳2^k步后所到达的结点，特别的，f[x][0]表示x的父结点那么由上述推论：f[x][k]=f[f[x][k-1]][k-1]

.然后我们再递归地向下处理。这就是预处理的部分.

然后，我们只需要先让x跳到与y深度相同(这里默认x的深度大于y)，然后，x，y再同时向上跳，直到x，y相遇前的最后一步，那么，此时f[x][0]==f[y][0]==LCA(x,y)

整个算法也就结束啦，下面直接上代码:

题目：

给定一棵 n 个点的树，Q 个询问，每次询问点 x 到点 y两点之间的距离。

输入

第一行一个正整数 n ，表示这棵树有 n个节点；

接下来 n−1 行，每行两个整数 x,y 表示 x,y 之间有一条连边；

然后一个整数 Q，表示有Q 个询问；

接下来 Q 行每行两个整数x,y 表示询问 x 到 y 的距离。

输出

输出 Q 行，每行表示每个询问的答案。

样例输入

6
1 2
1 3
2 4
2 5
3 6
2
2 6
5 6

样例输出

3
4

提示

对于全部数据，1≤n,m≤105,1≤x,y≤n

程序来啦QAQ：

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<algorithm>
  4 #include<cstdlib>
  5 #define ONE 100010
  6
  7 using namespace std;
  8
  9 struct node {
 10     int u;
 11     int v;
 12     int next;
 13 };
 14
 15 node edge[ONE<<1];  //邻接表存数据
 16 int dep[ONE],f[ONE][30],next[ONE],cnt_edge=0,n,q,x,y;
 17
 18 //int Read()   快读可以加速，可以学一下
 19 //{
 20 //    int f=1,k=0;
 21 //    char c=getchar();
 22 //    while(c!='-'&&(c<'0'||c>'9')) c=getchar();
 23 //    if(c=='-')
 24 //    {
 25 //        f=-1;
 26 //        c=getchar();
 27 //    }
 28 //    while(c>='0'&&c<='9')
 29 //    {
 30 //        k=(k<<3)+(k<<1)+c-48;
 31 //        c=getchar();
 32 //    }
 33 //    return f*k;
 34 //}
 35
 36 void add_edge(int u,int v)
 37 {
 38     edge[++cnt_edge].u=u;
 39     edge[cnt_edge].v=v;
 40     edge[cnt_edge].next=next[u];
 41     next[u]=cnt_edge;
 42 }
 43
 44 void Deal_first(int u,int fa)//预处理
 45 {
 46     dep[u]=dep[fa]+1;//处理当前结点深度，方便后面向上跳时使用
 47
 48     for(int i=0;i<=19;i++) f[u][i+1]=f[f[u][i]][i];//类似于二分的思想
 49
 50     for(int i=next[u];i;i=edge[i].next)
 51     {
 52         int to=edge[i].v;
 53         if(to==fa) continue;//注意判断回边，不能跳到自己的父亲结点
 54         f[to][0]=u;
 55         Deal_first(to,u);//向下递归
 56     }
 57 }
 58
 59 int LCA(int x,int y)  //求解LCA
 60 {
 61     if(dep[x]<dep[y]) swap(x,y); //保证x的深度大于y的深度
 62     for(int i=20;i>=0;i--)        //这里注意要先跳大步再跳小步，类似于用天平称量物体时先放大砝码再放小砝码是一个道理
 63     {
 64         if(dep[f[x][i]]>=dep[y]) x=f[x][i];
 65
 66         if(x==y) return x;
 67     }
 68     for(int i=20;i>=0;i--)
 69     {
 70         if(f[x][i]!=f[y][i])
 71         {
 72             x=f[x][i];
 73             y=f[y][i];
 74         }
 75     }
 76     return f[x][0];
 77 }
 78
 79 int get_dis(int x,int y)
 80 {
 81     return  dep[x]+dep[y]-2*dep[LCA(x,y)];
 82 }
 83
 84 int main ()
 85 {
 86     //n=Read();
 87     scanf("%d",&n);
 88     for(int i=1;i<n;i++)
 89     {
 90         //x=Read();y=Read();
 91         scanf("%d%d",&x,&y);
 92         add_edge(x,y);
 93         add_edge(y,x);
 94     }
 95
 96     Deal_first(1,0);
 97
 98     //q=Read();
 99     scanf("%d",&q);
100     while(q--)
101     {
102 //        x=Read();
103 //        y=Read();
104         scanf("%d%d",&x,&y);
105         printf("%d\n",get_dis(x,y));
106     }
107     return 0;
108 }

看完了点个赞再走哦亲~（手动开心o(￣▽￣)o）