牛客 51011 可达性统计（拓扑排序，bitset)

牛客 51011 可达性统计（拓扑排序，bitset)

题意：

给一个 n个点，m条边的有向无环图，分别统计每个点出发能够到达的点的数量(包括自身) \(n,m\le30000\).

样例：

10 10
3 8
2 3
2 5
5 9
5 9
2 3
3 9
4 8
2 10
4 9

题解：

想要统计每个点能够出发到达的点数量，如果一个一个点来搜索计算的话，那么复杂度将会变成 \(O(n^2)\),所以我们要换个角度思考，在访问每一个点的时候，考虑由哪个点可以到达它，所以我们可以反向建边，按照图拓扑排序的顺序进行访问，将自身的贡献传递给自己的临点。

​ 但是计算贡献的时候，要考虑重复的计算，如下图（已经是反向建边了），D点访问过后，A和C点的贡献都为2，如果再一次 访问完A和C后，B的贡献就会变成5，显然的多计算了一次D的贡献。

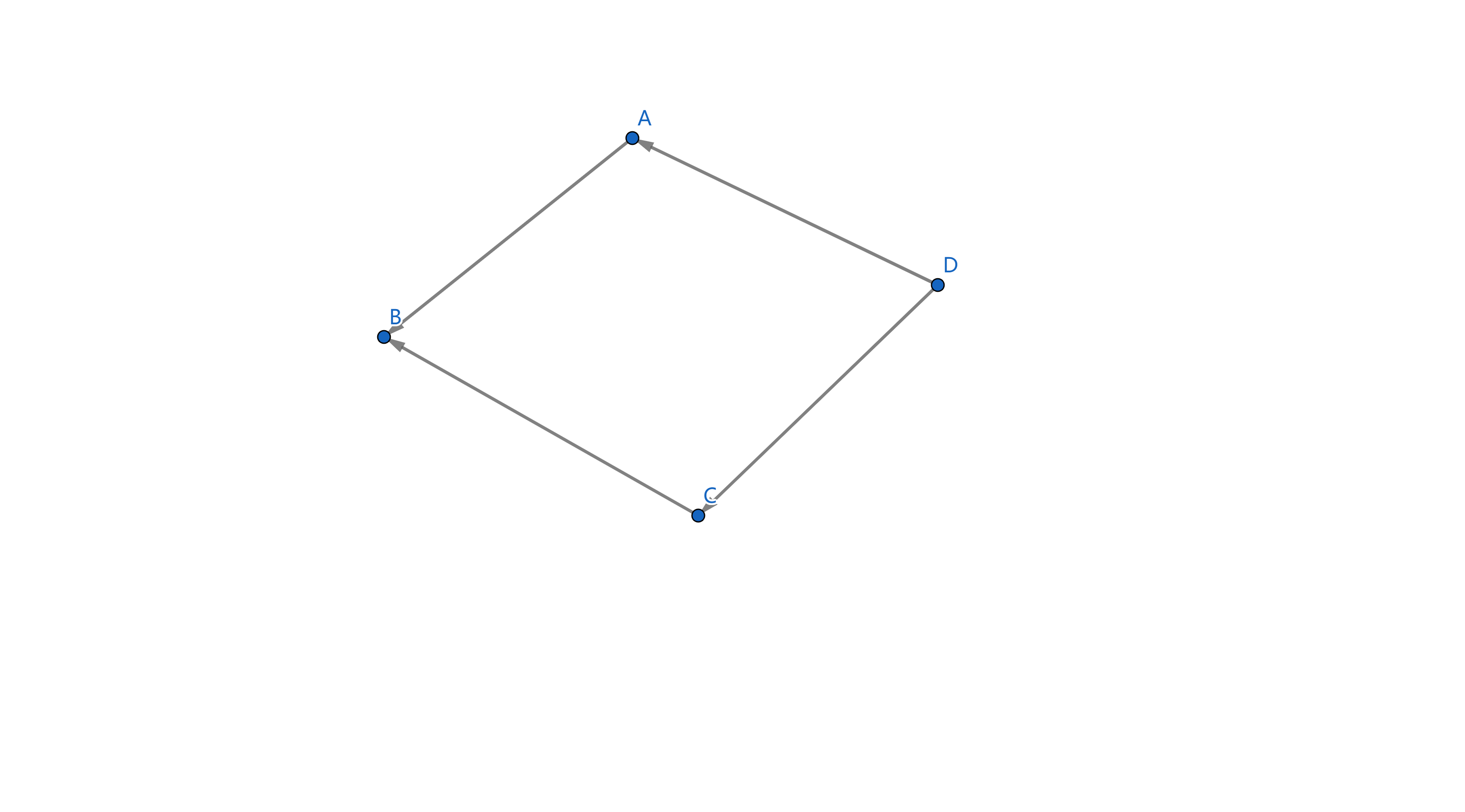
​ 在这里我们可以引入二进制位来避免这种情况发生，也就是用一个数字的二进制数来表示一个点的贡献，这个二进制数第i位为 \(i\)，则代表这个点可以到达 \(i\)，设上图的A，B，C，D点分别为点1，2，3，4.那么起始的点1，2，3，4的贡献可以记录为 2，4，8，16.其实是他们的二进制位的第一位，第二位，第三位，第四位设位1了，那么点A的贡献将为 \(val_A | val_D\)=2|16 =18，C的贡献为 \(valD|valC\)=16|8 =24.这样点B的贡献将为\(valA|valB|valC\)=18 | 24 | 4=30.这代表着B点可以到达第一个点，第二个，第三个点，第四个点。由于或运算的关系，D的贡献不会重复计算。不过这里还有一个问题是由于数据规模的原因我们不能直接用数字来表示二进制位的贡献，因此我们要引入bitset。

bitset

bitset是C++提供的一个模板类，原型为 template<size_t N>class bitset。参数是bitset的二进制位的个数。

bitset<6>B;//这里我们定义了一个长度为40的bitset，它的每一位都是bool类型，占内存1bit
B[2]=1;//每一个位置都可以通过下标来访问以及进行修改。
bitset<6>C(string("101"));//我们还可以用一个只包含0和1字符的string类来初始话这个bitset,
//这里bitset的值依次为000101.是string的长度超过bitset的长度，字符串后面的字符会被舍弃掉。
C.count();//输出C种为1的bool元素的个数。这里结果为2.
C.reset();//将C的所有的位数全部置为1.
B = B|C;//同时支持  或，与，异或 这种位运算。要保证他们的长度要相同。

​ 有了bitset的这些操作后，思路就很明显了，按照拓扑排序的顺序访问，每一次用bitset来传递贡献，最后输出每个bitset种为1的bool元素的个数。

struct P{int x;int y;P(){}P(int _x,int _y):x(_x),y(_y){}};
vector<int>ege[maxn];
bitset<maxn>cnt[maxn];
set<P>S;
int in[maxn]={0};
bool operator<(const P a,const P b){//
    if(a.x==b.x)return a.y<b.y;
    return a.x<b.x;
}
void solve(){
    int n,m;scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++){
        int x,y;scanf("%d %d",&x,&y);
        if(S.count(P(x,y)))continue;//将重复元素筛掉。
        S.insert(P(x,y));
        ++in[x];
        ege[y].push_back(x);
    }
    for(int i=1;i<=n;i++)cnt[i][i]=1;//将第i个bitset的第i位初始化1.
    queue<int>q;
    for(int i=1;i<=n;i++){
        if(in[i]==0)q.push(i);
    }
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int v:ege[u]){
            --in[v];
            cnt[v] = cnt[v]|cnt[u];//用或运算将u的贡献传递给v。
            if(in[v]==0)q.push(v);
        }
    }
    for(int i=1;i<=n;i++)printf("%d\n",cnt[i].count());
}