NOIP 2016 组合数问题 题解

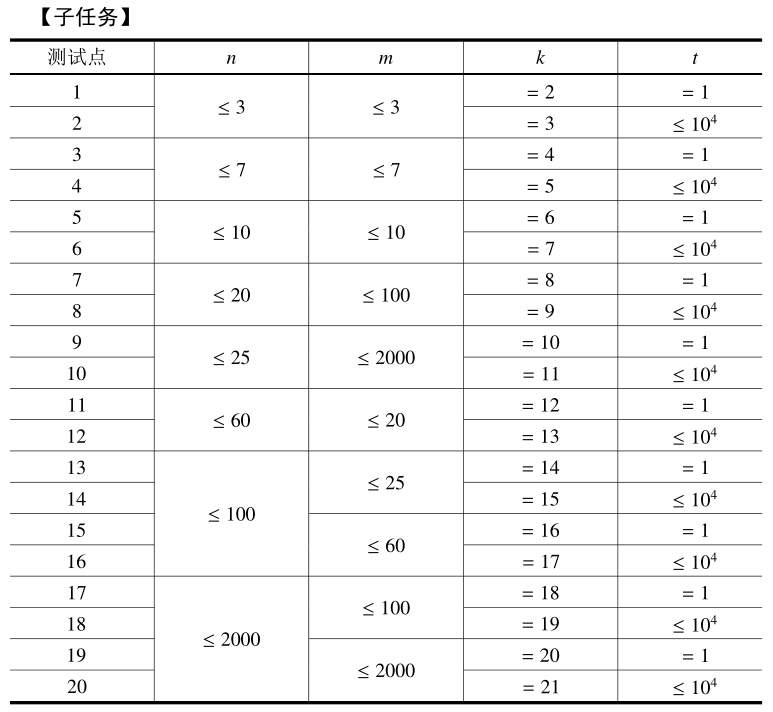
一道sb题目,注意范围，可打表解决，打出杨辉三角，在用前缀和求解即可

代码(一维前缀和)

#include<bits/stdc++.h>
using namespace std;
int n,m,t,k,ans,a[2010][2010],b[2010][2010];
int main(){
	scanf("%d %d",&t,&k);
	a[0][0]=1%k;
	a[1][0]=1%k;
	a[1][1]=1%k;
	for(int i=2;i<=2005;++i){
		for(int j=0;j<=i;++j){
			a[i][j]=(a[i-1][j]+a[i-1][j-1])%k;
		}
	}
	for(int i=0;i<=2005;++i){
		for(int j=0;j<=i;++j){
			b[i][j]+=b[i][j-1];
			if(a[i][j]==0) b[i][j]++;
		}
	}
	while(t--){
		scanf("%d %d",&n,&m);
		ans=0;
		for(int i=0;i<=n;++i){
			int j=min(m,i);
			ans+=b[i][j];
		}
		printf("%d\n",ans);
	}
	return 0;
}

二维

#include<bits/stdc++.h>
using namespace std;
int n,m,t,k,a[2010][2010],b[2010][2010];
int main(){
	scanf("%d %d",&t,&k);
	a[0][0]=1;
	a[1][0]=1;
	a[1][1]=1;
	for(int i=2;i<=2005;++i){
		for(int j=0;j<=i;++j){
			a[i][j]=(a[i-1][j]+a[i-1][j-1])%k;
			if(a[i][j]==0) b[i][j]=1;
		}
	}
	for(int i=1;i<=2005;++i){
		for(int j=1;j<=2005;++j){
			b[i][j]=b[i][j-1]+b[i-1][j]-b[i-1][j-1]+b[i][j];
		}
	}
	while(t--){
		scanf("%d %d",&m,&n);
		n=min(n,m);
		printf("%d\n",b[m][n]);
	}
	return 0;
}