HDU 4832 Chess（DP+组合数学）（2014年百度之星程序设计大赛 - 初赛（第二轮））

Problem Description

　　小度和小良最近又迷上了下棋。棋盘一共有N行M列，我们可以把左上角的格子定为(1,1)，右下角的格子定为(N,M)。在他们的规则中，“王”在棋盘上的走法遵循十字路线。也就是说，如果“王”当前在(x,y)点，小度在下一步可以移动到(x+1, y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2) 这八个点中的任意一个。

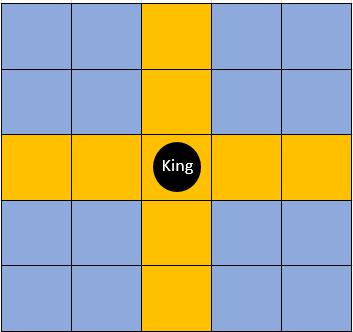
　　图1 黄色部分为棋子所控制的范围
　　小度觉得每次都是小良赢，没意思。为了难倒小良，他想出了这样一个问题：如果一开始“王”在(x₀,y₀)点，小良对“王”连续移动恰好K步，一共可以有多少种不同的移动方案？两种方案相同，当且仅当它们的K次移动全部都是一样的。也就是说，先向左再向右移动，和先向右再向左移动被认为是不同的方案。
　　小良被难倒了。你能写程序解决这个问题吗？

 

Input

输入包括多组数据。输入数据的第一行是一个整数T(T≤10)，表示测试数据的组数。
每组测试数据只包括一行，为五个整数N,M,K,x₀,y₀。(1≤N,M,K≤1000,1≤x₀≤N,1≤y₀≤M)

 

Output

对于第k组数据，第一行输出Case #k:，第二行输出所求的方案数。由于答案可能非常大，你只需要输出结果对9999991取模之后的值即可。

 

题目大意：略。

思路：很容易想到一个朴素的DP，dp[i][j][k]代表走k步走到坐标(i, j)的方案数，复杂度为O(nmk)，超时的节奏。

仔细想想，可以发现竖着走和横着走是独立的，于是分开考虑。

k步中，选i步横着走，那么有k-i步是竖着走的，设sumx[i]为横着走i步的方案数，sumy[k-i]为竖着走k-i步的方案数。

那么 ans = sum{c[k][i] * sumx[i] * sumy[k-i], 0 ≤ i ≤ k}，其中c[k][i]为组合数，意味在k步中选择i步横着走。

其中sumx[]可以用dp[i][j]表示走k步走到坐标i（一维）的方案数，复杂度为O(nk)，sum[y]同理。

于是总复杂度降到O(nk + mk)。

 

代码（750MS）;

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 #include <vector>
 using namespace std;
 typedef long long LL;

 const int MOD = ;
 const int MAXN = ;

 int f[] = {-, -, , };

 int n, m, k, x0, y0, T;
 int dpx[MAXN][MAXN], dpy[MAXN][MAXN];
 int sumx[MAXN], sumy[MAXN];
 int c[MAXN][MAXN];

 void initc() {
     int n = ;
     c[][] = ;
     for(int i = ; i <= n; ++i) {
         c[i][] = ;
         for(int j = ; j <= i; ++j)
             c[i][j] = (c[i - ][j] + c[i - ][j - ]) % MOD;
     }
 }

 bool check(int x, int n) {
     return  <= x && x <= n;
 }

 int solve() {
     memset(dpx, , sizeof(dpx));
     dpx[][x0] = ;
     for(int p = ; p <= k; ++p) {
         for(int i = ; i <= n; ++i) {
             for(int v = ; v < ; ++v) {
                 int t = i + f[v];
                 if(check(t, n)) dpx[p][t] = (dpx[p][t] + dpx[p - ][i]) % MOD;
             }
         }
     }

     memset(sumx, , sizeof(sumx));
     for(int i = ; i <= k; ++i) {
         for(int j = ; j <= n; ++j) sumx[i] = (sumx[i] + dpx[i][j]) % MOD;
     }

     memset(dpy, , sizeof(dpy));
     dpy[][y0] = ;
     for(int p = ; p <= k; ++p) {
         for(int i = ; i <= m; ++i) {
             for(int v = ; v < ; ++v) {
                 int t = i + f[v];
                 if(check(t, m)) dpy[p][t] = (dpy[p][t] + dpy[p - ][i]) % MOD;
             }
         }
     }

     memset(sumy, , sizeof(sumy));
     for(int i = ; i <= k; ++i) {
         for(int j = ; j <= m; ++j) sumy[i] = (sumy[i] + dpy[i][j]) % MOD;
     }

     LL ans = ;
     for(int i = ; i <= k; ++i)
         ans = (ans + LL(c[k][i]) * sumx[i] % MOD * sumy[k - i]) % MOD;

     return (int)ans;
 }

 int main() {
     initc();
     //cout<<c[1000][1000]<<endl;
     scanf("%d", &T);
     for(int t = ; t <= T; ++t) {
         scanf("%d%d%d%d%d", &n, &m, &k, &x0, &y0);
         printf("Case #%d:\n", t);
         printf("%d\n", solve());
     }
 }