51nod 1100 斜率最大
可以用三个点简单证明斜率最大的直线两个点!
#include <bits/stdc++.h>
#define MAXN 10010
using namespace std;
struct Node{
int x, y, number;
}gg[MAXN];
bool cmp(Node a, Node b){
return a.x<b.x;
}
int main(void){
std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int n;
cin >> n;
for(int i=0; i<n; i++){
cin >> gg[i].x >> gg[i].y;
gg[i].number=i+1;
}
sort(gg, gg+n, cmp);
queue<int> node1, node2;
double cnt=0, cc=0;
for(int i=1; i<n; i++){
cnt=(gg[i].y-gg[i-1].y)*1.0/(gg[i].x-gg[i-1].x);
if(cnt>cc){
cc=cnt;
while(!node1.empty()){
node1.pop();
}
while(!node2.empty()){
node2.pop();
}
node1.push(gg[i-1].number);
node2.push(gg[i].number);
}else if(cnt==cc){
node1.push(gg[i-1].number);
node2.push(gg[i].number);
}
}
while(!node1.empty()){
cout << node1.front() << " " << node2.front() << endl;
node1.pop();
node2.pop();
}
return 0;
}51nod 1100 斜率最大的更多相关文章
- 51 Nod 1100 斜率最大
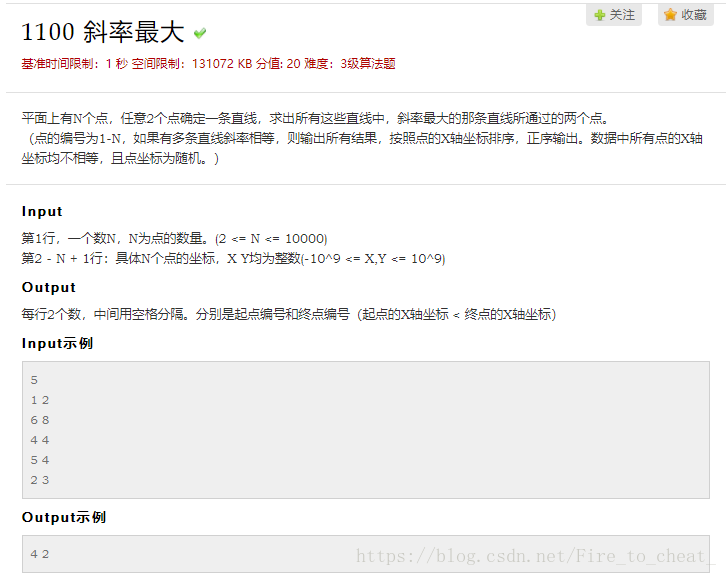
1100 斜率最大 基准时间限制:1 秒 空间限制:131072 KB 分值: 20 难度:3级算法题 收藏 关注 平面上有N个点,任意2个点确定一条直线,求出所有这些直线中,斜率最大的那条直线 ...
- 【51nod 1100】斜率最大
Description 平面上有N个点,任意2个点确定一条直线,求出所有这些直线中,斜率最大的那条直线所通过的两个点. (点的编号为1-N,如果有多条直线斜率相等,则输出所有结果,按照点的X轴坐标 ...
- 51Nod P1100 斜率最大
传送门: https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1100 由于2 <= N <= 10000, 所以 ...
- 51Nod - 1107 斜率小于0的连线数量
二维平面上N个点之间共有C(n,2)条连线.求这C(n,2)条线中斜率小于0的线的数量. 二维平面上的一个点,根据对应的X Y坐标可以表示为(X,Y).例如:(2,3) (3,4) (1,5) (4, ...
- 【51NOD】斜率最大
[题解]通过画图易得结论:最大斜率一定出现在相邻两点之间. #include<cstdio> #include<algorithm> #include<cstring&g ...
- 51nod 1107 斜率小于零连线数量 特调逆序数
逆序数的神题.... 居然是逆序数 居然用逆序数过的 提示...按照X从小到大排列,之后统计Y的逆序数... 之后,得到的答案就是传说中的解(斜率小于零) #include<bits/stdc+ ...
- 51NOD——N 1107 斜率小于0的连线数量
https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1107 基准时间限制:1 秒 空间限制:131072 KB 分值: 40 ...
- 51nod 1451 合法三角形 判斜率去重,时间复杂度O(n^2)
题目: 这题我WA了3次,那3次是用向量求角度去重算的,不知道错在哪了,不得不换思路. 第4次用斜率去重一次就过了. 注意:n定义成long long,不然求C(3,n)时会溢出. 代码: #incl ...
- 51nod 1488 帕斯卡小三角 斜率优化
思路:斜率优化 提交:\(2\)次 错因:二分写挂 题解: 首先观察可知, 对于点\(f(X,Y)\),一定是由某个点\((1,p)\),先向下走,再向右下走. 并且有个显然的性质,若从\((1,p) ...
随机推荐
- python统一的换行符,实现跨平台
6 PEP 278: Universal Newline Support The three major operating systems used today are Microsoft Wind ...
- linux设备驱动归纳总结
前言: (总结已经基本写完,这段时间我会从新排版和修正.错误总会有的,望能指正!) 前段时间学习了嵌入式驱动,趁着没开始找工作,这段时间我会每天抽出时间来复习. 我的总结是根据学习时的笔记(李杨老师授 ...
- sudo 用户添加
sudo 用户添加 /etc/sudoers 在 ## Allow root to run any commands anywhere root ALL=(ALL) ALL 下面加上 xxx ...
- linuxc线程信号-pthread_cond_wait理解
pthread_cond_wait(pthread_cond_t *cond, pthread_mutex_t*mutex)函数 传入的參数mutex用于保护条件,由于我们在调用pthread_con ...
- Android开发——本地验证码的简易实现
0. 前言 验证码无处不在.有人问我,你知道达芬奇password以下是什么吗,对.答案就是达芬奇验证码. 验证码一个最基本的作用就是防止恶意暴力破解登录,防止不间断的登录尝试,事实上能够在se ...
- android 浮动窗体学习笔记及个人理解(仿360手机助手)
很感谢原文作者 http://blog.csdn.net/guolin_blog/article/details/8689140 经自己理解 程序执行界面例如以下图: 1.程序入口界面 2.小浮动窗体 ...
- 他人第三方库在linux上的安装
1.下载tar.gz等压缩包 2.解压 3.安装 4.确保路径
- Codeforces 755 F. PolandBall and Gifts 多重背包+贪心
F. PolandBall and Gifts It's Christmas time! PolandBall and his friends will be giving themselves ...
- Delphi指向函数指针的指针
type TFunc=procedure; procedure MyFunc; begin ShowMessage('Run my func'); end; procedure TForm1.Butt ...
- 【转】Android 6.0 Marsmallow BLE : Connection Parameters
原文网址:http://stackoverflow.com/questions/34617061/android-6-0-marsmallow-ble-connection-parameters Th ...