Test for Job 图上的动态规划（DAG）

Test for Job

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 11399		Accepted: 2697

Description

Mr.Dog was fired by his company. In order to support his family, he must find a new job as soon as possible. Nowadays, It's hard to have a job, since there are swelling numbers of the unemployed. So some companies often use hard tests for their recruitment.

The test is like this: starting from a source-city, you may pass through some directed roads to reach another city. Each time you reach a city, you can earn some profit or pay some fee, Let this process continue until you reach a target-city. The boss will compute the expense you spent for your trip and the profit you have just obtained. Finally, he will decide whether you can be hired.

In order to get the job, Mr.Dog managed to obtain the knowledge of the net profit V_i of all cities he may reach (a negative V_i indicates that money is spent rather than gained) and the connection between cities. A city with no roads leading to it is a source-city and a city with no roads leading to other cities is a target-city. The mission of Mr.Dog is to start from a source-city and choose a route leading to a target-city through which he can get the maximum profit.

Input

The input file includes several test cases. 
The first line of each test case contains 2 integers n and m(1 ≤ n ≤ 100000, 0 ≤ m ≤ 1000000) indicating the number of cities and roads. 
The next n lines each contain a single integer. The ith line describes the net profit of the city i, V_i (0 ≤ |V_i| ≤ 20000) 
The next m lines each contain two integers x, y indicating that there is a road leads from city x to city y. It is guaranteed that each road appears exactly once, and there is no way to return to a previous city. 

Output

The output file contains one line for each test cases, in which contains an integer indicating the maximum profit Dog is able to obtain (or the minimum expenditure to spend)

Sample Input

6 5
1
2
2
3
3
4
1 2
1 3
2 4
3 4
5 6

Sample Output

7

Hint

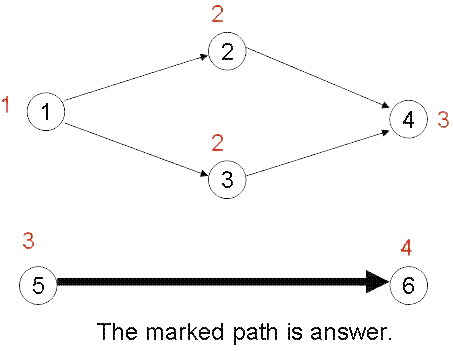
Source

POJ Monthly--2007.07.08, 落叶飞雪

 

按照拓扑序列进行DP

#include <iostream>
#include <string>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <deque>
#include <map>
#include <stack>
#include <cstring>
using namespace std;
typedef long long LL;
#define INF 0x3f3f3f3f
#define MAXN 200000+9
#define MAXM 2000000 + 9

struct edge
{
    LL next, v, cost;
}E[MAXM];
LL n, m;
LL head[MAXN], tot;
LL cnt[MAXN], topsort[MAXN];
LL val[MAXN], dist[MAXN],out[MAXN];
void init()
{
    tot = ;
    memset(head, -, sizeof(head));
    memset(cnt, , sizeof(cnt));
    memset(out, , sizeof(out));
}
void addedge(LL f, LL t, LL d)
{
    E[tot].v = t;
    E[tot].cost = d;
    E[tot].next = head[f];
    head[f] = tot++;
}
LL Topsort()
{
    LL p = ;
    for (LL i = ; i <= n; i++)
    {
        if (cnt[i] == )
            dist[i] = val[i], topsort[p++] = i, cnt[i]--;
        else
            dist[i] = -INF;
    }
    for (LL i = ; i < p; i++)
    {
        for (LL j = head[topsort[i]]; j != -; j = E[j].next)
        {
            LL v = E[j].v;
            dist[v] = max(dist[v], dist[topsort[i]] + E[j].cost);
            if (--cnt[v] == )
                topsort[p++] = v;
        }
    }
    LL ans = -INF;
    for (int i = ; i <= n; i++)
        if (!out[i])
            ans = max(ans, dist[i]);
    return ans;

}

int main()
{
    while (scanf("%lld%lld", &n, &m) != EOF)
    {
        init();
        for (int i = ; i <= n; i++)
            scanf("%lld", &val[i]);
        LL f, t;
        for (int i = ; i <= m; i++)
        {
            scanf("%lld%lld", &f, &t);
            addedge(f, t, val[t]);
            cnt[t]++;
            out[f]++;
        }
        printf("%lld\n", Topsort());
    }
}