Reactor Cooling（无源汇有上下界网络流）

194. Reactor Cooling

time limit per test: 0.5 sec. 
memory limit per test: 65536 KB

input: standard 
output: standard

The terrorist group leaded by a well known international terrorist Ben Bladen is buliding a nuclear reactor to produce plutonium for the nuclear bomb they are planning to create. Being the wicked computer genius of this group, you are responsible for developing the cooling system for the reactor.

The cooling system of the reactor consists of the number of pipes that special cooling liquid flows by. Pipes are connected at special points, called nodes, each pipe has the starting node and the end point. The liquid must flow by the pipe from its start point to its end point and not in the opposite direction.

Let the nodes be numbered from 1 to N. The cooling system must be designed so that the liquid is circulating by the pipes and the amount of the liquid coming to each node (in the unit of time) is equal to the amount of liquid leaving the node. That is, if we designate the amount of liquid going by the pipe from i-th node to j-th as f _ij, (put f _ij = 0 if there is no pipe from node i to node j), for each i the following condition must hold:

sum(j=1..N, f _ij) = sum(j=1..N, f _ji)

Each pipe has some finite capacity, therefore for each i and j connected by the pipe must be f _ij ≤ c _ij where c _ij is the capacity of the pipe. To provide sufficient cooling, the amount of the liquid flowing by the pipe going from i-th to j-th nodes must be at least l _ij, thus it must be f _ij ≥ l _ij.

Given c _ij and l _ij for all pipes, find the amount f _ij, satisfying the conditions specified above. 

Input

The first line of the input file contains the number N (1 ≤ N ≤ 200) - the number of nodes and and M — the number of pipes. The following M lines contain four integer number each - i, j, l _ij and c _ij each. There is at most one pipe connecting any two nodes and 0 ≤ l _ij ≤ c _ij ≤ 10 ⁵ for all pipes. No pipe connects a node to itself. If there is a pipe from i-th node to j-th, there is no pipe from j-th node to i-th. 

Output

On the first line of the output file print YES if there is the way to carry out reactor cooling and NO if there is none. In the first case M integers must follow, k-th number being the amount of liquid flowing by the k-th pipe. Pipes are numbered as they are given in the input file. 

Sample test(s)

Input

 

 

Test #1

4 6 
1 2 1 2 
2 3 1 2 
3 4 1 2 
4 1 1 2 
1 3 1 2 
4 2 1 2

Test #2

4 6 
1 2 1 3 
2 3 1 3 
3 4 1 3 
4 1 1 3 
1 3 1 3 
4 2 1 3 

 

 

Output

 

 

Test #1

NO

Test #2

YES 
1 
2 
3 
2 
1 
1 

 

就是裸的吧，可以满足输出YES，并且每条的流量，如果不行，输出no。

建边：

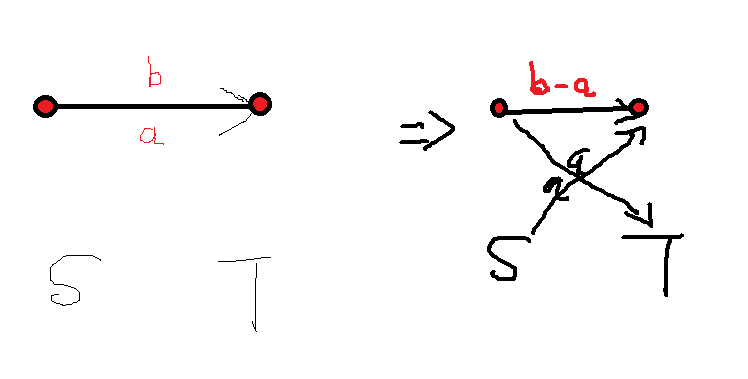
然后跑一次最大流，判断是不是大于等于sum（即最小下界流量和），然后输出即可。