Codeforces Round #319 (Div. 1)C. Points on Plane 分块思想

                                                                          C. Points on Plane

On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and bis said to be the following value: 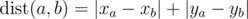 (the distance calculated by such formula is called Manhattan distance).

We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value .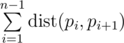

Find some hamiltonian path with a length of no more than 25 × 108. Note that you do not have to minimize the path length.

Input

The first line contains integer n (1 ≤ n ≤ 106).

The i + 1-th line contains the coordinates of the i-th point: xi and yi (0 ≤ xi, yi ≤ 106).

It is guaranteed that no two points coincide.

Output

Print the permutation of numbers pi from 1 to n — the sought Hamiltonian path. The permutation must meet the inequality .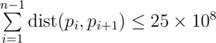

If there are multiple possible answers, print any of them.

It is guaranteed that the answer exists.

Sample test(s)

input

5
0 7
8 10
3 4
5 0
9 12

output

4 3 1 2 5 

Note

In the sample test the total distance is:

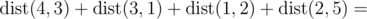
(|5 - 3| + |0 - 4|) + (|3 - 0| + |4 - 7|) + (|0 - 8| + |7 - 10|) + (|8 - 9| + |10 - 12|) = 2 + 4 + 3 + 3 + 8 + 3 + 1 + 2 = 26

题意：给你一个1e6*1e6的图，上面有n个点，定义dist距离，求一条任意路径使得dist总和不超过 25*1e8

题解：分块思想，讲1e6分成1000份，x(1000*(k-1)<=x<=1000*k)每份对y单调递增，对于一份，在y轴上产生价值最多1e6，1000份就是1e9.

在x轴上，假设所有点分布在一份上，则最多是1e9，如果任意分布最多也是1e9

总的来说就是2*1e9，可行

///
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll;
#define mem(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,127,sizeof(a));
#define TS printf("111111\n");
#define FOR(i,a,b) for( int i=a;i<=b;i++)
#define FORJ(i,a,b) for(int i=a;i>=b;i--)
#define READ(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define inf 100000
inline ll read()
{
    ll x=,f=;
    char ch=getchar();
    while(ch<''||ch>'')
    {
        if(ch=='-')f=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=x*+ch-'';
        ch=getchar();
    }
    return x*f;
}
//****************************************
#define maxn 1000000+10

pair<pair<int ,int >,int > P[maxn];
int main()
{

    int n=read();
    int x,y;
    FOR(i,,n)
    {
         x=read();
         y=read();
        P[i].first.first=x/;//注意
         P[i].first.second=y;
         P[i].second=i;
    }
    sort(P+,P+n+);
    FOR(i,,n)
    {
        cout<<P[i].second<<" ";
    }
    return ;
}

代码