HDU 1724 Ellipse 自适应simpson积分

simpson公式是用于积分求解的比较简单的方法（有模板都简单……

下面是simpson公式（很明显 这个公式的证明我并不会……

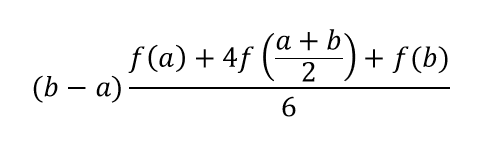（盗图……

因为一段函数基本不可能很规则 所以我们要用自适应积分的方法

找了一道很水的积分题试试模板……

关于simpson要*15 网上有很具体的证明过程……

（细节移步至：http://www2.math.umd.edu/~mariakc/teaching/adaptive.pdf

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<string>
 #define cl(a,b) memset(a,b,sizeof(a))
 #define debug(x) cerr<<#x<<"=="<<(x)<<endl
 using namespace std;
 typedef long long ll;
 const double eps=1e-;

 double a,b,l,r;

 double f(double x)
 {//原函数
     return sqrt((b*b)*(-(x*x)/(a*a)));
 }

 double simpson(double a,double b)
 {//simpson公式
     double c=a+(b-a)/;
     return (f(a)+*f(c)+f(b))*(b-a)/;
 }

 double asr(double a,double b,double eps,double A)
 {//自适应部分
     double c=a+(b-a)/;
     double L=simpson(a,c);
     double R=simpson(c,b);
     if(fabs(L+R-A)<=*eps) return L+R+(L+R-A)/15.0;//判断是否满足精度
     return asr(a,c,eps/,L)+asr(c,b,eps/,R);
 }

 double asr(double a,double b,double eps)
 {//积分
     return asr(a,b,eps,simpson(a,b));
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%lf%lf%lf%lf",&a,&b,&l,&r);
         printf("%.3f\n",*asr(l,r,eps));
     }
     return ;
 }
 /*

 2
 2 1 -2 2
 2 1 0 2

 */

当然上面是数学不好的同学做的

数学好的同学是这么做的……

 #include<cstdio>
 #include<cmath>
 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         double a,b,l,r;
         scanf("%lf%lf%lf%lf",&a,&b,&l,&r);
         double ans=acos(l/a);
         double ant=acos(r/a);
         double re=a*b*((sin(*ant)-sin(*ans))/-(ant-ans));
         printf("%.3f\n",re);
     }
     return ;
 }

（毫无疑问 这个同学不是我……