「题解」NWRRC2017 Grand Test

本文将同步发布于：

题目

题目链接：洛谷 P7025、gym101612G。

题意概述

给你一张有 $n$ 个点 $m$ 条边的无向图，无重边无自环，请你求出两个点 $s,t$ 使得 $s,t$ 之间有三条不重合的简单路径。

$1\leq\sum n,\sum m\leq 10^5$

题解

探究图的性质

考虑到本题是无向图，我们不难想到一个引理。

引理：无向图的 dfs 树上只存在树边和返祖边。

考虑到 dfs 树中只会存在树边、返祖边、横叉边，因此我们只需要证明无向图的 dfs 树上不存在横叉边即可。

考虑反证法。

假设存在一条横叉边 $(u,v)$，目前遍历到 $u$，$v$ 在之前被访问过，根据横叉边的定义，$v$ 不是 $u$ 的祖先。

根据深度优先搜索的深度优先原则，此时一定访问完了所有与 $v$ 相连的节点，但 $u$ 却未被访问到，造成矛盾，假设不成立，引理得证。

利用性质构造方案

考虑到 dfs 树上只有额外的返祖边，我们不难构造出一种方案。

对于一个点 $u$，如果它的两棵子树内存在两个节点 $x,y$ 使得有两条返祖边 $(x,p_1),(y,p_2)$ 满足 $p_1,p_2$ 是节点 $u$ 的祖先，则 $s=p_1,t=u$ 符合条件。

画成图长下面这样：

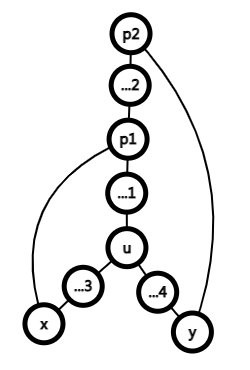
充分性十分显然，下面我们考虑证明必要性。即不存在上述情况，也有满足条件的三条路径和两个节点。

不难发现这是不可能的，因为只要存在起点与终点，它们在 dfs 树上必然是祖先关系，因此一定满足上述情况，矛盾。

因此我们证明了这个条件的充分必要性，用 tarjan 算法判定即可。时间复杂度 $\Theta(n)$。

参考程序

#include<bits/stdc++.h>

using namespace std;

#define reg register

typedef long long ll;

#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)

static char buf[1<<21],*p1=buf,*p2=buf;

#define flush() (fwrite(wbuf,1,wp1,stdout),wp1=0)

#define putchar(c) (wp1==wp2&&(flush(),0),wbuf[wp1++]=c)

static char wbuf[1<<21];int wp1;const int wp2=1<<21;

inline int read(void){

	reg char ch=getchar();

	reg int res=0;

	while(!isdigit(ch))ch=getchar();

	while(isdigit(ch))res=10*res+(ch^'0'),ch=getchar();

	return res;

}

inline void write(reg int x){

	static char buf[32];

	reg int p=-1;

	if(x<0) x=-x,putchar('-');

	if(!x) putchar('0');

	else while(x) buf[++p]=(x%10)^'0',x/=10;

	while(~p) putchar(buf[p--]);

	return;

}

const int MAXN=1e5+5;

int n,m;

vector<int> G[MAXN];

int fa[MAXN];

int tim,dfn[MAXN],rnk[MAXN],low[MAXN],ed[MAXN],clow[MAXN],ced[MAXN];

int s,t;

inline void tarjan(reg int u,reg int father){

	fa[u]=father;

	dfn[u]=low[u]=clow[u]=++tim;

	rnk[tim]=u;

	ed[u]=ced[u]=u;

	for(int v:G[u])

		if(v!=father){

			if(!dfn[v]){

				tarjan(v,u);

				if(low[v]<low[u]){

					clow[u]=low[u],ced[u]=ed[u];

					low[u]=low[v],ed[u]=ed[v];

				}

				else if(low[v]<clow[u])

					clow[u]=low[v],ced[u]=ed[v];

			}

			else{

				if(dfn[v]<low[u]){

					clow[u]=low[u],ced[u]=ed[u];

					low[u]=dfn[v],ed[u]=u;

				}

				else if(dfn[v]<clow[u])

					clow[u]=dfn[v],ced[u]=u;

			}

		}

	if(!s&&!t&&clow[u]<dfn[u])

		s=u,t=rnk[clow[u]];

	return;

}

inline vector<int> getPath(reg int son,int father){

	vector<int> res;

	for(int p=son;p!=father;p=fa[p])

		res.push_back(p);

	res.push_back(father);

	return res;

}

inline vector<int> reverse(vector<int> a){

	reverse(a.begin(),a.end());

	return a;

}

inline vector<int> merge(vector<int> a,vector<int> b){

	a.insert(a.end(),b.begin(),b.end());

	return a;

}

int main(void){

	reg int T=read();

	while(T--){

		n=read(),m=read();

		for(reg int i=1;i<=n;++i)

			G[i].clear();

		for(reg int i=1;i<=m;++i){

			static int u,v;

			u=read(),v=read();

			G[u].push_back(v),G[v].push_back(u);

		}

		tim=0,fill(dfn+1,dfn+n+1,0);

		s=0,t=0;

		for(reg int i=1;i<=n;++i)

			if(!dfn[i])

				tarjan(i,0);

		if(!s&&!t)

			write(-1),putchar('\n');

		else{

			write(s),putchar(' '),write(t),putchar('\n');

			vector<int> ans1=getPath(s,t);

			write(ans1.size()),putchar(' ');

			for(reg int i=0,siz=ans1.size();i<siz;++i)

				write(ans1[i]),putchar(i==siz-1?'\n':' ');

			vector<int> ans2=merge(reverse(getPath(ed[s],s)),reverse(getPath(t,rnk[low[s]])));

			write(ans2.size()),putchar(' ');

			for(reg int i=0,siz=ans2.size();i<siz;++i)

				write(ans2[i]),putchar(i==siz-1?'\n':' ');

			vector<int> ans3=merge(reverse(getPath(ced[s],s)),getPath(rnk[clow[s]],rnk[clow[s]]));

			write(ans3.size()),putchar(' ');

			for(reg int i=0,siz=ans3.size();i<siz;++i)

				write(ans3[i]),putchar(i==siz-1?'\n':' ');

		}

	}

	flush();

	return 0;

}