Codeforces 1503E - 2-Coloring（组合数学）

Codeforces 题目传送门 & 洛谷题目传送门

考虑什么样的 2-染色方式是符合题目要求的，首先蓝、黄颜色所形成的连通块个数必须 \(\le 2\)，否则一定不合法，而显然如果两种颜色连通块个数都为 \(1\) 也不合法，以蓝色连通块个数为 \(1\)，黄色连通块个数为 \(2\) 为例，稍微画个图即可发现合法的染色方式都如下图所示：

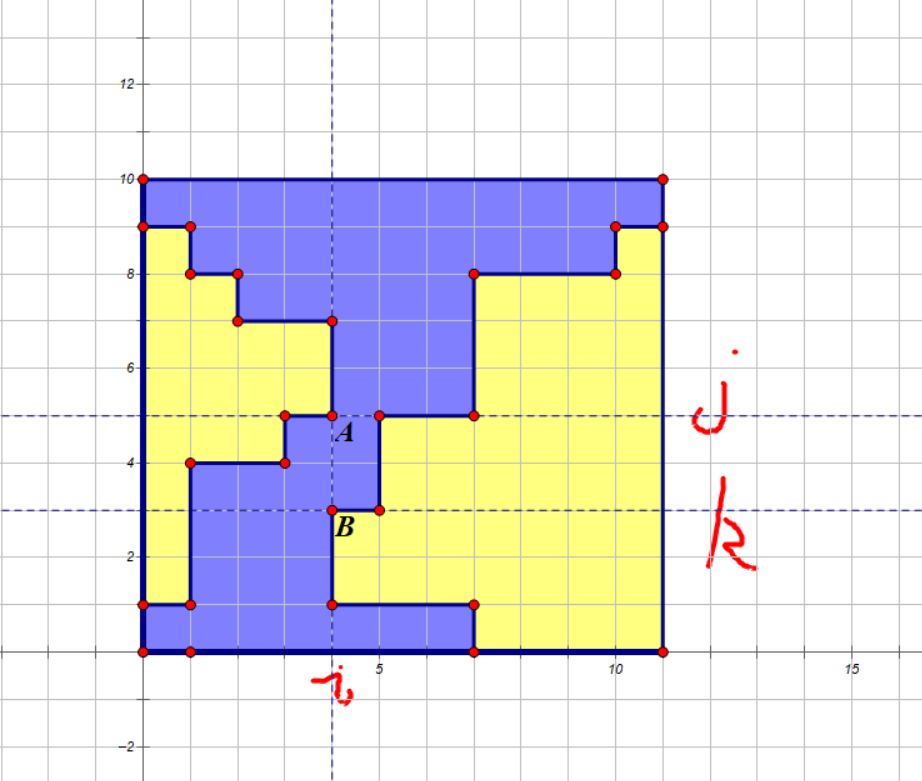
也就是说存在一个分割点 \(i\)，使得第一个连通块全部在第 \(i\) 列左侧，第二个连通块全部在第 \(i\) 列右侧，那么显然两个连通块与第 \(i\) 列的交点分别是一段不相交区间 \((l_1,r_1),(l_2,r_2)\)，我们假设第一个连通块的区间在第二个连通块的区间的上方，也就是如图所示的情况，那么我们假设 \(j=r_1,k=l_2\)（当然如果 \(j=k\) 蓝色连通块会被一分为二，也就是蓝色、黄色连通块个数都为 \(2\) 的情况），那么显然第一个连通块与直线 \(x=i\) 的交中最下方的点的坐标就是 \((j,i)\)（即图中的点 A），第二个连通块与直线 \(x=i\) 的交中最上方的点就是 \((k,i)\)（即图中的点 B）。接下来考虑怎样计算方案数，隔板法是肯定没问题的，不过这里有一种更简便的理解方式，以计算 \(A\) 左上角的方案数为例，它等价于从最左上角的点走到 \(A\) 的方案数，但由于 \(A\) 是这段区间中最下方的点，因此最后一步必须是向下走的，因此左上角的方案数就是从最左上角的点走到 \(A\) 上方的点的方案数，另外四块也同理，如图所示：

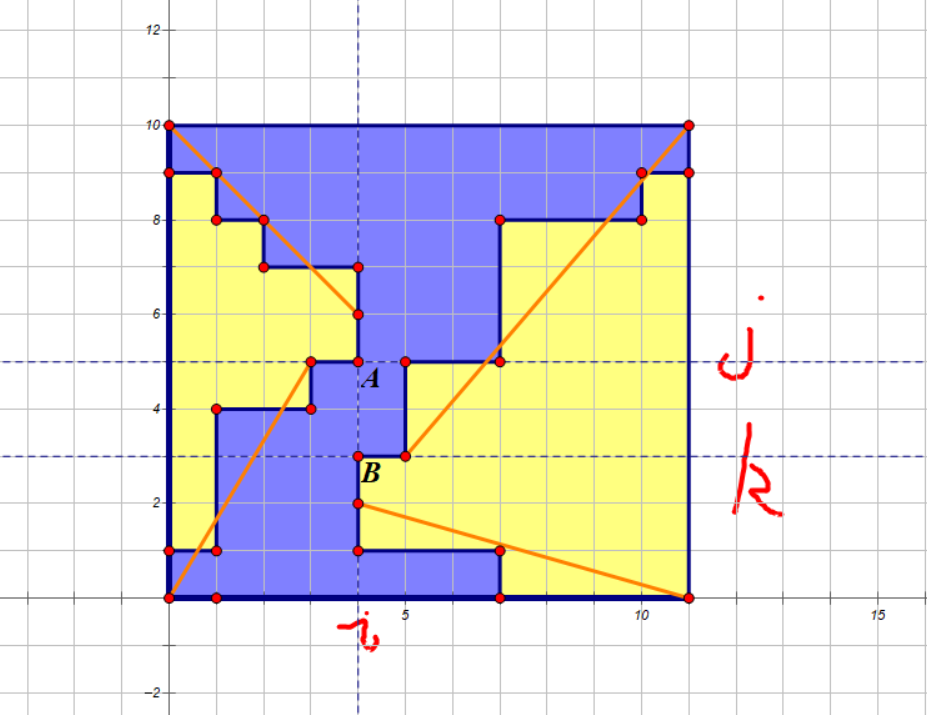
暴力枚举是 \(n^2m\) 的，通过前缀和优化可以做到 \(nm\)。对于 \((l_1,r_1)\) 在 \((l_2,r_2)\) 下方的情况只需乘个 \(2\) 即可，因为所有 \((l_1,r_1)\) 在 \((l_2,r_2)\) 上方的情况把它上下翻转都能够得到 \((l_1,r_1)\) 在 \((l_2,r_2)\) 下方的情况，因此它们构成了一个双射。对于蓝色连通块个数为 \(2\)，黄色连通块个数为 \(1\) 的情况其实很 simple，只需做整个网络关于 \(y=x\) 对称的图形即可，但是这样蓝色、黄色连通块个数都是 \(2\) 的情况会被算重，因此第二次计算的时候需要强制令 \(k-j\ge 1\)。

时间复杂度 \(\mathcal O(nm)\)

const int MAXN=1<<12;
const int MOD=998244353;
int n,m,fac[MAXN+5],ifac[MAXN+5],ans=0;
void init_fac(int n){
	for(int i=(fac[0]=ifac[0]=ifac[1]=1)+1;i<=n;i++) ifac[i]=1ll*ifac[MOD%i]*(MOD-MOD/i)%MOD;
	for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%MOD,ifac[i]=1ll*ifac[i-1]*ifac[i]%MOD;
}
int ways(int x,int y){return 1ll*fac[x+y]*ifac[x]%MOD*ifac[y]%MOD;}
int main(){
	scanf("%d%d",&n,&m);init_fac(MAXN);
	for(int i=1;i<=m-1;i++){
		int sum=0;
		for(int j=1;j<=n-1;j++){
			sum=(sum+1ll*ways(i,j-1)*ways(i-1,n-j))%MOD;
			ans=(ans+1ll*sum*ways(m-i-1,j)%MOD*ways(m-i,n-j-1))%MOD;
		}
	} n^=m^=n^=m;
	for(int i=1;i<=m-1;i++){
		int sum=0;
		for(int j=1;j<=n-1;j++){
			ans=(ans+1ll*sum*ways(m-i-1,j)%MOD*ways(m-i,n-j-1))%MOD;
			sum=(sum+1ll*ways(i,j-1)*ways(i-1,n-j))%MOD;
		}
	} printf("%d\n",(ans<<1)%MOD);
	return 0;
}