XDFZOI 月赛 201905 Sliver

组题人自己组完过后，才发现自己还是太弱了。。。

---

T1

简单模拟。

按照游戏规则直接模拟显然是不明智的，所以我们可以像石头剪刀布一样，将判断改变为检验。

同时，我们发现，一共只有48种牌，所以我们可以直接开一个数组记录一下，\(card[peo][col][tag]\)表示第\(peo\)个人，第\(col\)种颜色，第\(tag\)种牌型有多少张

然后，按照优先级，暴力枚举每个人的每一张牌，同时根据游戏规则进行检验，比如当此时仍有"+2"卡在传递时，除了"+2"和"turn"两种牌型牌型外其余任何牌型都不能出等等。

然后这个题目就解决啦！

Upd：有点锅，按照题意修改了一下题面（是我没表述清楚啦QAQ）

#include<bits/stdc++.h>
using namespace std;
int card[20][20][20];
int cnt[10],vis[10];
struct cc{
    int lei,tim,id;
}boom[10];
bool cmp(cc x,cc y)
{
    return x.lei==y.lei?x.tim<y.tim:x.lei<y.lei;
}
bool check(int col,int tag,int lstcol,int lsttag,int dl)
{
    if(lstcol==-1&&lsttag==-1) return 1;
    if(dl)
    {
        if((col==lstcol)&&(tag==12||tag==11)) return 1;
        return 0;
    }
    else
    {
        if(col==lstcol||(tag==lsttag&&tag!=11&&tag!=12)) return 1;
        else return 0;
    }
}
int main()
{
//  freopen("UnIon10.in","r",stdin);
//  freopen("UnIon10.out","w",stdout);
//  freopen("样例解释.out","w",stdout);
	int ggg=0;
    for(int i=1;i<=4;++i)
    {
        scanf("%d",&cnt[i]),boom[i].id=i,ggg+=cnt[i];
    }
    for(int i=1;i<=4;++i)
    {
        for(int j=1;j<=cnt[i];++j)
        {
            int a,b;
            scanf("%d%d",&a,&b);
            ++card[i][a][b];
        }
    }
    int nex=1,now=1,peo=4,dilei=0,lc=-1,lt=-1;
    int ti=0;
    if(!ggg)
	{
		printf("0 0 0 0 \nxiaoai\n");
		return 0;
	 }
    while(peo>1)
    {
//      printf("%d\n",peo);
        if(now==0) now=4;
        if(now==5) now=1;
        int flag=0;
        if(!cnt[now])
        {
            now+=nex;
            continue;
        }
        vis[now]=1;
        ++ti;
        for(int i=1;i<=4;++i)
        {
            for(int j=12;j>=1;--j)
            {
                if(card[now][i][j]&&check(i,j,lc,lt,dilei))
                {
                    flag=1;
//                  printf("%d %d %d\n",now,i,j);
                    --card[now][i][j];
                    --cnt[now];
                    lc=i;
                    lt=j;
                    if(j==12) nex=-nex;
                    if(j==11) dilei+=2;
                    break;
                }
            }
            if(flag) break;
        }
        if(!cnt[now]) --peo,boom[now].tim=ti;
        if(!flag) ++boom[now].lei,lc=-1,lt=-1,boom[now].lei+=dilei,dilei=0;
        now+=nex;
    }
    while(!cnt[now])
    {
    	now+=nex;
    	if(now==0) now=4;
        if(now==5) now=1;
	}
    boom[now].lei+=dilei;
    for(int i=1;i<=4;++i)
        boom[i].lei+=cnt[i],printf("%d ",boom[i].lei);
    sort(boom+1,boom+5,cmp);
    printf("\n");
    if(boom[1].id==1) puts("xiaoai");
    else if(boom[1].id==2) puts("Yoyo");
    else if(boom[1].id==3) puts("Siri");
    else if(boom[1].id==4) puts("Bixby");
    return 0;
}

---

T2

这是一道二合一的题目。

简单二分 （三分）+简单背包

首先，只要你学过背包就一定能看出这是一个背包问题，还是一个放满背包问题。

在这里就不细说了，简单讲一讲前面的部分

求

\[ f(x)=x^x
\]

已知\(f(x)\),求较小的\(x\)

首先，我们可以将这个函数的图像画出来 比赛时这么做的打死

可以很清晰的看到在这个函数当中有一个最低点，跟二次函数类似。

那，怎样求最低点呢？

标准解法：三分法

可以右转洛谷模板区

对于一个在\([l,r]\)区间上存在最值的函数\(f(x)\),都可以用三分法解决。

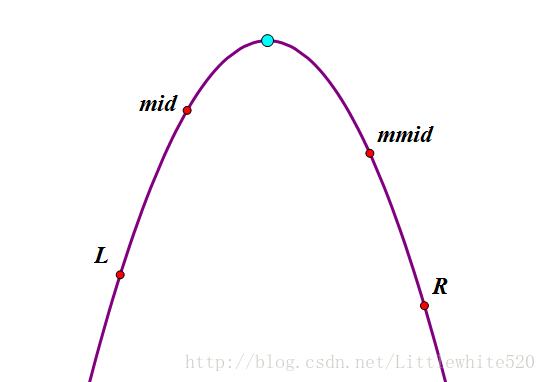
观察这张图，就可以轻松找到规律（转载声明，感谢图片）

1、当 f(mid) > f(mmid) 　　　　mmid 一定在白点的右边。

2、当 f(mid) < f(mmid) 　　　　　mid 一定在白点的左边。

然后就可以愉快的三分了

非标准解法：枚举法

我们将函数图像进一步放大，或者也可以通过函数有关的知识可以得到，这个最低点一定在0_{1之间，所以，题目要求保留5位小数，我们可以枚举6}7位小数，取其中得到的最小值，同样可以得到答案。

---

找到最低点之后，我们发现，在最低点左边的部分单调，在最低点右边的部分也单调，所以我们可以采取分段二分的方式，针对不同的数据范围，进行方向调整不同的二分，就可以求出每个小面包所需要的最低成本，然后以其为价值，进行dp即可。

于是这道题目也被解决了。

#include<bits/stdc++.h>
#define eps 1e-9
#define low 0.36787897
using namespace std;
const int maxn=200000;
int n;
long double l,r=20;
double fff(double x){return pow(x,x);}
double solve(double x)
{
	l=0,r=20;
    if(x<1)
	{
		r=low;
		while(r-l>eps)
		{
			double mid=(l+r)/2.0;
			if(fff(mid)>x) l=mid;
			else r=mid;
		}
		return l;
	}
	else
	{
		l=low;
		while(r-l>eps)
		{
			double mid=(l+r)/2.0;
			if(fff(mid)<x) l=mid;
			else r=mid;
		}
		return l;
	}
}
int c[maxn];
double v[maxn],f[maxn];
int opt;
int main()
{
	freopen("baker.in","r",stdin);
	freopen("baker.out","w",stdout);
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		scanf("%lf%d",&v[i],&c[i]),v[i]=solve(v[i]);
	for(int i=1;i<=20000;++i)
		f[i]=(double)998244353;
	f[0]=0;
	for(int i=1;i<=n;++i)
		for(int j=c[i];j<=20000;++j)
			f[j]=min(f[j],f[j-c[i]]+v[i]);
	for(int i=1;i<=m;++i)
	{
		scanf("%d",&opt);
		while(f[opt]==998244353&&opt>0) --opt;
		if(opt==0) printf("-1T^T1-\n");
		else printf("%d %.5lf\n",opt,f[opt]);
	}
    return 0;
}

---

T3

老实说，这是我扒的原题，因为解法太多，也有值得借鉴的地方，就搬过来了。

简化版题意：求一个区间内的众数，且出现次数在区间中超过区间长度的一半。

首先，因为我是分块讲课人，自然要让大家学以致用。

使用分块，可以得到80%左右的分数，因为空间开不下，时间也不够。

使用莫队，可以得到86分，剩下14分，被我卡掉了。

开不开心，激不激动？

---

首先介绍一个知识

摩尔投票法

非常通俗的说，两群人打架，里面每个人都属于某一个帮派，现在两两PK，若是同一个帮派则握手平局，否则便两人皆淘汰。这样的话，很自然的可以得出，只要某一个帮派人数超过了总人数的1/2,就可以赢得比赛胜利。

摩尔投票法就是这样一个思想。

由于作者时间所限，给出题目链接：

P2397

---

利用这种方法，可以轻松通过m=1的数据。

下面抛出一个问题，摩尔投票法具有可加性吗？

答案是肯定的。

那我们可以用什么进行维护呢？

当然是线段树辣！！

这个东西，我们在后面会进一步提到。

但是，用线段树维护并不能保证找到的一定是正确的解。

所以我们需要对每一个数字开一个vector，记录其位置，然后检验一下，不成功就输出0

时间复杂度为\(O(nlogn)\)

记得我在讲搜索的时候，讲了一种剪枝方法——随机化剪枝，从此很多人就走上了不归路。

更进一步

既然维护了线段树都需要检验，可不可以不维护，直接进行检验呢？

我们先来解决这样一个数学问题：一个口袋里10个球，5红，5蓝，连续摸n次（放回），一次都摸不到红球的概率是？

显然，答案为\(1/2^{n}\)

那么，是不是，只要n足够大，就可以看作一定能摸到呢？

对于本题来说，可以，如果你的n到达到了20，就已经超出了这个范围，可以看作无错。

于是这个题目就解决啦！！

原题链接：P3567

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=6e5+10;
vector<int> pos[maxn];
int v[maxn];
bool vis[maxn];
int s[maxn],cnt;
int random(int x)
{
    return 1ll*rand()*233%x;
}
int main()
{
//	freopen("randerlng.in","r",stdin);
//	freopen("randerlng.out","w",stdout);
    srand(time(0));
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i)
        scanf("%d",&v[i]),pos[v[i]].push_back(i);
    for(int i=1;i<=m;++i)
    {
        int x,y,flag=1;
        scanf("%d%d",&x,&y);
        for(int j=1;j<=20;++j)
        {
            int now=v[x+random((y-x+1))];
            if(vis[now]) continue;
            vis[now]=1;
            s[++cnt]=now;
            if(pos[now].size()<=((y-x+1)/2)) continue;
            int num=upper_bound(pos[now].begin(),pos[now].end(),y)-lower_bound(pos[now].begin(),pos[now].end(),x);
            if(num>(y-x+1)/2)
            {
                printf("%d\n",now);
                flag=0;
                break;
            }
        }
        while(cnt) vis[s[cnt]]=0,--cnt;
        if(flag)
            puts("0");
    }
    return 0;
}

拓展

按照作者的本意，本题还应该要支持修改操作(但是由于用现有知识复杂度不严格取消了)，应该怎么办呢？

按照随机的做法，我们只需要将vector中的保存的位置删除再添加即可，但这样做是\(O(n)\)的。

于是我们需要用平衡树来解决这个问题。

具体见此题：P3765

于是这场比赛就完了。

总结

这场比赛还是太水啦

估计：每人至少150pts+？

下次一定会难一点的，毕竟地球还在流浪嘛（手动狗头）