[Matlab]二维统计分析图实例

常见的二维统计分析图形：

• bar(x,y,选项)　条形图
• stairs(x,y,选项)　阶梯图
• stem(x,y,选项)　杆图
• fill(x1,y1,选项1,x2,y2,选项2,……)　填充图

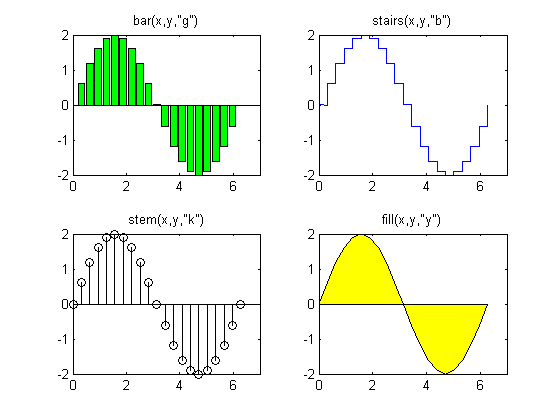
实例：绘制曲线y=2sin(x)的统计图

x = 0:pi/10:2*pi;
y = 2*sin(x);
subplot(2,2,1);
bar(x,y,'g');
title('bar(x,y,"g")');
axis([0,7,-2,2]);
subplot(2,2,2);
stairs(x,y,'b');
title('stairs(x,y,"b")');
axis([0,7,-2,2]);
subplot(2,2,3);
stem(x,y,'k');
title('stem(x,y,"k")');
axis([0,7,-2,2]);
subplot(2,2,4);
fill(x,y,'y');
title('fill(x,y,"y")');
axis([0,7,-2,2]);

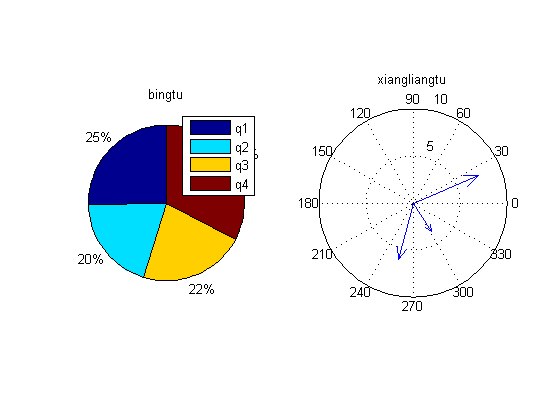
实例：绘制饼图和复数的向量图

subplot(1,2,1);
pie([2347,1827,2043,3025]);
title('bingtu');
legend('q1','q2','q3','q4');
subplot(1,2,2);
compass([7+2.9i,2-3i,-1.5-6i]);
title('xiangliangtu');

​