eetcode必要技巧--动态规划(一)

首先我们要搞清楚什么是动态规划

动态规划是运筹学中用于求解决策过程中的最优化数学方法。当然，我们在这里关注的是作为一种算法设计技术，作为一种使用多阶段决策过程最优的通用方法。

当然这个很难理解,但是按照本人的理解.

实际上就是一个种类的问题.

在这个问题中,我们只需要列出一个方程,就能用递归的方法解决大部分呢问题.

(突然看到一个不错的消息)

动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。

既然是要求最值，核心问题是什么呢？求解动态规划的核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值呗。

作者：labuladong

链接：https://leetcode-cn.com/problems/coin-change/solution/dong-tai-gui-hua-tao-lu-xiang-jie-by-wei-lai-bu-ke/

来源：力扣（LeetCode）

总结一下,就是对整个内容进行穷举操作,恰好这种穷举操作有着大量的可重复性,可以利用递归来解决.

个人认为动态规划有俩个核心

1. 递归
2. 冗余处理

我们就用leetcode中的零钱兑换.

给定不同面额的硬币 coins 和一个总金额 amount。

编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11

输出: 3

解释: 11 = 5 + 5 + 1

示例 2:

输入: coins = [2], amount = 3

输出: -1

说明:

你可以认为每种硬币的数量是无限的。

这里还要引申一下,一开始我想到的算法使用amount(总金额)%5(coins中最大的硬币)得出余数(在这里假设为remainder).

再用remainder(上面得出的数)%2(coins中第二大的硬币面值)不断地循环下去.

据说这叫贪心算法.

这个无疑是错误的.比如[1,5,11] 凑15

那么按照这个贪心算法的唯一结果是 一个11和4个1

但是正确的答案是三个5

这就是这种算法的局限性

说回正题

要想解决问题,我们就必须分析这个问题.

我们就必须化出解决这个问题的穷举图像

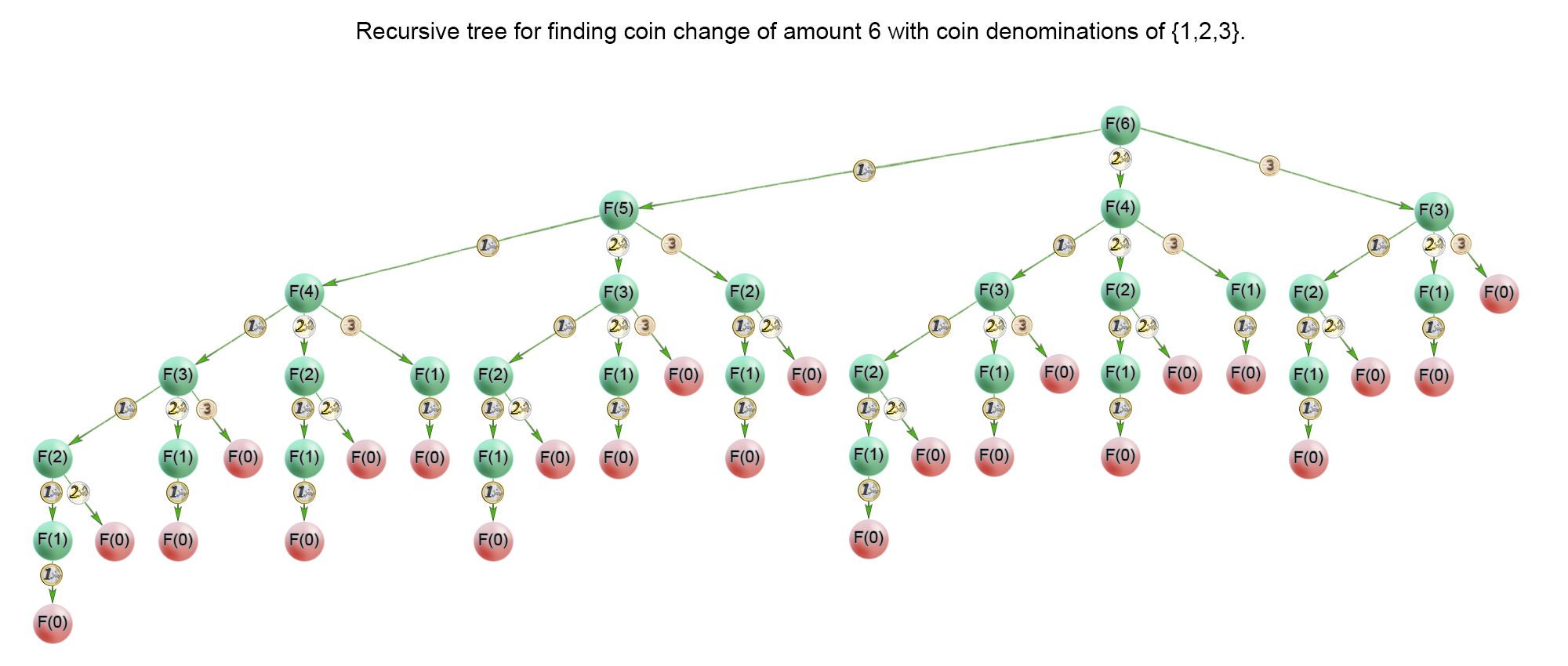
这里说一下,这个也是从leetcode上拿的.

我们看这个图像,最上面有一行小字,翻译如下:

emmm英语不好,挑重点说吧

[1,2,3]种面值的币子

凑6

我们会发现如果要遍历这个树,就会发现每一个节点执行的操作实际上都是大同小异的,而且面对的数据也都是大同小异的(都是那三个数,1,2,3都不会变化)

所以也正是因为如此.我们可以采用.递归的方式.

在这里就要说到处理这种方式的诀窍了.如果按照递归的思路一直深究下去,那么唯一的结果就是蒙圈.

毕竟太深入,太复杂了.

可是我们要意识到,其实这个算法再每一个节点上都是相同的,都可以用一样的算法.于是我们只要列出第一层和第二层之间的关系就可以用这个关系为突破口,想办法用递归实现这个问题.

F(S)=F(S-C)+1;

F(S):所要求的目标->最少的硬币个数

S:总金额

c:(所用)最后一个硬币的面值

eg:

   在最顶层 6节点开始有以下三种情况

   F(6)=F(6-1)+1=F(5)+1
   F(6)=F(6-2)+1=F(4)+1
   F(6)=F(6-3)+1=F(3)+1
   我们要知道其中F(5)因为也是一个函数所以,也会向下裂变化为
   F(5)=F(5-1)+1
   F(5)=F(5-2)+1
   F(5)=F(5-3)+1
   然后面还可以裂变,直到s-c=0或者s-c<0为止(这就是我们迭代的停止条件,s-c>0)

   这就是用迭代形成了一个遍历的过程.相比while这种方式,方便了很多倍.[这个遍历的实质上得出的是每一条可能出现的路径所要消耗的硬币数量]
   但是我们遍历的目的是为了找出一条最短的路径,使用最少的硬币数量,所以我们需要对其进行比较.
   也就是在
   --A代码块
   F(6)=F(6-1)+1=F(5)+1
   F(6)=F(6-2)+1=F(4)+1
   F(6)=F(6-3)+1=F(3)+1
   ---
   这三个可能中选择最小的一个.
   F(S)是最少硬币的个数.
   而如果要求出这三个我们就要知道F(5,4,3)[简写]中谁最小.于是这就要到了,我们要知道
   F(5)=F(5-1)+1
   F(5)=F(5-2)+1
   F(5)=F(5-3)+1
   种谁最小的问题.
   完全是一摸一样的,这就是递归最好的温床.

//coins 硬币面值(是个数组,在迭代过程中从不变化)
    //rem 总值就是S
    //count[] 记录的信息(这个是为了防止重复计算的问题)
//这个for就是找出A代码块中那个线路最小的步骤,存在min中
 for (int coin : coins) {
      int res = coinChange(coins, rem - coin, count);

      //F(S)=F(S-C)+1;
      //rem-coin对应的就是S-C

      if (res >= 0 && res < min)
      //min的结果实际上就是最小的res+1就是F(S).而res实际上是
        min = 1 + res;
        //F(S)=F(S-C)+1;
        //res=function(coins,S-C,count);
        //min=function(coins,S-C,count)+1;
    }
    代码看到这里我们就知道了这个部分我们已经完全实现了这个式子中所要求的一切.
    我们所要做的其实就是复刻你列出的式子.
    不必想的太深.
    当你发现他们每个节点高度的统一性的时候,其实只要解决其中一个节点,剩下的节点就都解决了.

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/coin-change/solution/322-ling-qian-dui-huan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这里贴一下完整的代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        //  if(amount<1)
          return coinChange(coins,amount,new int[amount]);
    }

    在这里我们会发现我们的要想递归就只能拿这个函数制作递归,但是s-c就无法实现了,所以我们只能重载一个.让这个最终返回内容.

    //coins 硬币面值
    //rem 总值
    //count[] 记录的信息
    private int coinChange(int [] coins,int rem,int [] count){
            if(rem==0) return 0;//解决输入不合理
            if(rem<0)return -1;//解决输入合理
            if(count[rem-1]!=0){return count[rem-1];}//如果以前已经有了记录,就返回被记录的数值
            int min=Integer.MAX_VALUE;
            for(int i=0;i<coins.length;i++){
                int res=coinChange(coins,rem-coins[i],count);//递归,如果以前有了相关的内容会直接反回
                //如果是最小的,那么就加1,作为最少币数
                if(res>=0&&min>res){
                    min=res+1;
                }
            }
            //min有没有被改变,要是改变了就不会是原值,自然回min
            count[rem - 1] = (min == Integer.MAX_VALUE) ? -1 : min;
            return count[rem - 1];
    }
}