蓝桥杯---地宫取宝（记忆搜索=搜索+dp）

题目网址：http://lx.lanqiao.org/problem.page?gpid=T120

问题描述

　　X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。



　　地宫的入口在左上角，出口在右下角。



　　小明被带到地宫的入口，国王要求他只能向右或向下行走。



　　走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。



　　当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。



　　请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。

输入格式

　　输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)



　　接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值

输出格式

　　要求输出一个整数，表示正好取k个宝贝的行动方案数。该数字可能很大，输出它对 1000000007 取模的结果。

样例输入

2 2 2

1 2

2 1

样例输出

2

样例输入

2 3 2

1 2 3

2 1 5

样例输出

14



题目的意思很简单，就是用深搜的方式来找出到底有多少路径，但是开始的时候虽然一眼就认定了是深度搜索，但是还真的不知道怎么搜，因为碰到不能捡的物品就不知道该怎么处理了，不深搜吧，肯定之后有符合条件的，这样的话就会落掉很多情况，但是搜的话好像也是不知道该如何是好，最后我甚至是想到把不管什么情况都深搜，如果能捡起来，就都捡起来然后在改变这个点出现的最大值，之后查找这么多种选择出k个所构成的组合数来解决，但是之后想到这样的话，如果拿了这个物品，由于修改了其最大值，这样的话会对之后的选择造成影响，利用组合数来实现根本是不行的，这样的话这条思路又中断了。。。

贴一下开始结果不正确的代码，长一下记性：

#include <iostream>
#include <cstdio>
#include <cstring>
#define MAXN 1100
#define MOD 100000007
using namespace std;
int count = 0,sum=0;
int m,n,k,  a[55][55];
long long  gcd ( long long  x,long long  y){
	if(y==0) return x>y?x:y;
	int t=x%y;
	while(t){  x=y,y=t,t=x%y;   }
	return y;
}
long long C(int a,int b){
	long long mu=1,zi=1;
	long long int n=b<a-b?b:a-b;
	for(int i=1,te=a;i<=n;i++,te--){
		mu*=te;
		zi*=i;
		long long int temp = gcd(mu,zi);
		mu/=temp;
		zi/=temp;
	}
	return mu/zi;
}
void dfs(int i,int j,int max){
	if(i==m-1&&j==n-1) {
		int mark=0;
	    if(a[i][j]>max)
	       count++,mark=1;
	    if(count>=k){   sum=(sum+C(count,k))%MOD ;     }//   cout<<count<<' ';
	     if(mark)
	       count--;
	  return ;
	}
	int mark=0;
	if(a[i][j]>max)  {  max=a[i][j],count++,mark=1;	 }
	if(i+1<m)
	  dfs(i+1,j,max);
	if(j+1<n)
    	dfs(i,j+1,max);
	if(mark)
	  count--;
}
int main()
{
    scanf("%d%d%d",&m,&n,&k);
    for(int i=0;i<m;i++)
       for(int j=0;j<n;j++)
         scanf("%d",&a[i][j]);
    dfs(0,0,0);
    cout<<sum;
    return 0;
}

之后才发现可以用动态规划的形式来深搜，比如这道题的话就是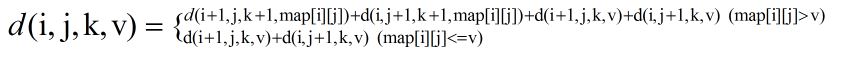

这里的V是指当前所走的路径中的物品价值的最大值，这样的话就完全可以通过不同状态的转换来完成深搜了，好像理解起来也是比较合乎情理的，事实证明这样的思路也是对的。。。



（PS：现在递归起来好像还不习惯用传参数的方式来做判断，用一个全体变量这样的话每次都会在函数开始的时候修改，在函数退出的时候再还原，突然感觉这样写出来的程序就和多层循环的嵌套一样了，完全没有运用到递归中局部变量的优越性，以后用递归的时候还是判断有哪些状态会影响到深度搜索的路径，就直接把他加为传参变量，直接用于状态判断，（这也是接下来所运用的记忆搜索=深搜+dp），这样思路应该会更加清晰了 吧，虽然现在才发现这个问题有点白痴，但是。。。好像也没有什么但是了吧）

#include <stdio.h>
#include <string.h>
#define N 1000000007
int n,m,k;
int map[50][50];

int dfs(int x,int y,int num,int max)//当前位置   拥有宝物的数量 拥有的宝物的最大值
 {
     if(x==n&&y==m){//到达出口
         if( num==k||(num==k-1&&max<map[x][y]) )  //到达右下角，（1）可能不算右下角的也正好，（2）如果右下角的比当前的大，算上这一个如果正好也可以增加路径
		    return  1;  //满足条件 当前点到目标有1种方案
         else
		 return  0;//不满足条件 当前点到目标有0种方案
     }
     long long s=0;
     if(x+1<=n){         //可以向下走
         if (max<map[x][y])
             s+=dfs(x+1,y,num+1,map[x][y]);
         s+=dfs(x+1,y,num,max);
     }
     if(y+1<=m){         //可以向右走
         if (max<map[x][y])
             s+=dfs(x,y+1,num+1,map[x][y]);
        s+=dfs(x,y+1,num,max);
     }
     return  s%N;
 }
 int main(){
     scanf("%d%d%d",&n,&m,&k);
     for (int i = 1;i<=n;i++)//初始地宫
         for (int j = 1; j <=m; j++)
             scanf("%d",&map[i][j]);
     printf("%d", dfs(1,1,0,-1));
     return 0;
 }

提交贴图：





果然还是完美的TL了，原因好像很简单了，因为深搜本来就是一件在时间复杂度上很消耗时间的算法了，现在再由于状态的区分明显复杂（每次进入一种状态最坏需要按照四条路径搜索，这可以在状态转移的方程中明显的看出来），这样的话好像就更加浪费了，所以果断超时。。。



这样的话就引出下面一个从来没用用到过的模型了。。。

第一次做记忆搜索的题目，开始的时候还不太清楚用数组干什么，后来才发现是用来记忆状态的、



先贴一下百度上的名词解释：

记忆化搜索：算法上依然是搜索的流程，但是搜索到的一些解用动态规划的那种思想和模式作一些保存。

一般说来，动态规划总要遍历所有的状态，而搜索可以排除一些无效状态。

更重要的是搜索还可以剪枝，可能剪去大量不必要的状态，因此在空间开销上往往比动态规划要低很多。

记忆化算法在求解的时候还是按着自顶向下的顺序，但是每求解一个状态，就将它的解保存下来，

以后再次遇到这个状态的时候，就不必重新求解了。

这种方法综合了搜索和动态规划两方面的优点，因而还是很有实用价值的。

结合这道题来说就是在碰到以前用过的状态的时候直接用打出的表的值就好了，这样的话就节约了不少时间了。。。

（这个题好像长了不少见识，虽然用来好长时间才做出来。。。）

#include <stdio.h>
#include <string.h>
#define N 1000000007
  int n,m,k;
  int map[50][50];
  int dp[50][50][15][15];//dp数组中记录的是状态   xy坐标 拥有宝物数量 拥有宝物的最大值(这4个可以详尽唯一的描述没一种可能)
                          //如dp[3][4][5][6]=7 即当在map[3][4]且身上有5件宝物 宝物的最大值是6 是到达终点有7中路径

  int dfs(int x,int y,int num,int max)//当前位置   拥有宝物的数量 拥有的宝物的最大值
 {
     if (dp[x][y][num][max+1]!=-1)//判断这个状态是否已经走过，如果走过就直接用记录的数值计算//因为宝物有可能为0所以定义max时用最小值-1 这就导致无法作为下标使用  实际上如果测试数据中宝物价值没有0
	                               //将所有的+1 去掉也是可以的   这里的话如果去掉肯定是有些数据不对的，不信可以提交试一下，根本过不了
         return dp[x][y][num][max+1];
       //记忆化的记忆就指的是上面

     if(x==n&&y==m){//到达出口
         if( num==k||(num==k-1&&max<map[x][y]) )  //到达右下角，（1）可能不算右下角的也正好，（2）如果右下角的比当前的大，算上这一个如果正好也可以增加路径
		    return dp[x][y][num][max+1]=1;  //满足条件 当前点到目标有1种方案
         else
		 return dp[x][y][num][max+1]=0;//不满足条件 当前点到目标有0种方案
     }
     long long s=0;
     if(x+1<=n){         //可以向下走
         if (max<map[x][y])
             s+=dfs(x+1,y,num+1,map[x][y]);//当前位置   拥有宝物的数量 拥有的宝物的最大值
         s+=dfs(x+1,y,num,max);            //当前位置   拥有宝物的数量 拥有的宝物的最大值
     }
     if(y+1<=m){         //可以向右走
         if (max<map[x][y])
             s+=dfs(x,y+1,num+1,map[x][y]);//当前位置   拥有宝物的数量 拥有的宝物的最大值
        s+=dfs(x,y+1,num,max);             //当前位置   拥有宝物的数量 拥有的宝物的最大值
     }
     return dp[x][y][num][max+1]=s%N;
 }
 int main(){
     scanf("%d%d%d",&n,&m,&k);
     for (int i = 1;i<=n;i++)//初始地宫
         for (int j = 1; j <=m; j++)
             scanf("%d",&map[i][j]);
     memset(dp,-1,sizeof(dp));
     dfs(1,1,0,-1);
     printf("%d",dp[1][1][0][0]);

     return 0;
 }

因此记忆搜索时从后向前搜索的。。。