如何用Python来处理数据表的长宽转换（图文详解）

　　不多说，直接上干货！

　　很多地方都需用到这个知识点，比如Tableau里。   通常可以采取如python 和 r来作为数据处理的前期。

Tableau学习系列之Tableau如何通过数据透视表方式读取数据文件（图文详解）

　　　数据长宽转换是很常用的需求，特别是当是从Excel中导入的汇总表时，常常需要转换成一维表（长数据）才能提供给图表函数或者模型使用。

python中，我这里只讲两个函数：

• melt #数据宽转长

• pivot_table #数据长转宽

　　Python中的Pandas包提供了与R语言中reshape2包内几乎同名的melt函数来对数据进行塑型（宽转长）操作，甚至连内部参数都保持了一致的风格。

import pandas as pd
import numpy as np

mydata=pd.DataFrame({
"Name":["苹果","谷歌","脸书","亚马逊","腾讯"],
"Conpany":["Apple","Google","Facebook","Amozon","Tencent"],
"Sale2013":[,,,,],
"Sale2014":[,,,,],
"Sale2015":[,,,,],
"Sale2016":[,,,,]
       })

mydata1=mydata.melt(
id_vars=["Name","Conpany"],   #要保留的主字段
var_name="Year",                     #拉长的分类变量
value_name="Sale"                  #拉长的度量值名称
        )

　　除此之外，我了解到还可以通过stack、wide_to_long函数来进行宽转长，但是个人觉得melt函数比较直观一些，也与R语言中的数据宽转长用法一致，推荐使用。

　　奇怪的是我好像没有在pandas中找到对应melt的数据长转宽函数（R语言中都是成对出现的）。还在Python中提供了非常便捷的数据透视表操作函数，刚开始就已经说过是，长数据转宽数据就是数据透视的过程（自然宽转长就可以被称为逆透视咯，PowerBI也是这么称呼的）。

　　pandas中的数据透视表函数提供如同Excel原生透视表一样的使用体验，即行标签、列标签、度量值等操作，根据使用规则，行列主要操作维度指标，值主要操作度量指标。

　　那么以上长数据mydata1就可以通过这种方式实现透视。

mydata1.pivot_table(
index=["Name","Conpany"],    #行索引（可以使多个类别变量）
columns=["Year"],                   #列索引（可以使多个类别变量）
values=["Sale"]                       #值（一般是度量指标）
     )

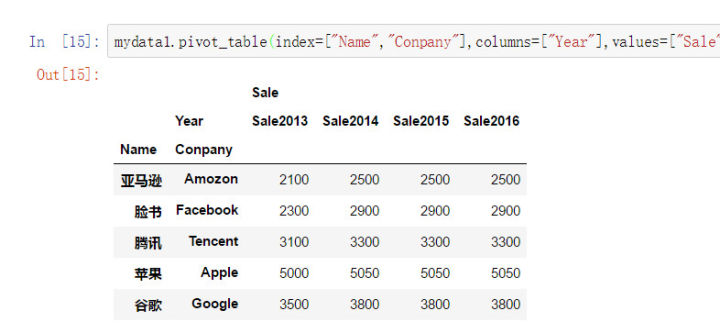
　　 通常这种操作也可以借助堆栈函数来达到同样的目的。(但是使用stack\unstack需要额外设置多索引，灰常麻烦，所以不是很推荐，有兴趣可以查看pandas中的stack/unstack方法，这里不再赘述)。　　

欢迎大家，加入我的微信公众号：大数据躺过的坑        人工智能躺过的坑

 

 

 

同时，大家可以关注我的个人博客：

   http://www.cnblogs.com/zlslch/   和     http://www.cnblogs.com/lchzls/      http://www.cnblogs.com/sunnyDream/   

   详情请见：http://www.cnblogs.com/zlslch/p/7473861.html

　　人生苦短，我愿分享。本公众号将秉持活到老学到老学习无休止的交流分享开源精神，汇聚于互联网和个人学习工作的精华干货知识，一切来于互联网，反馈回互联网。
　　目前研究领域：大数据、机器学习、深度学习、人工智能、数据挖掘、数据分析。 语言涉及：Java、Scala、Python、Shell、Linux等 。同时还涉及平常所使用的手机、电脑和互联网上的使用技巧、问题和实用软件。 只要你一直关注和呆在群里，每天必须有收获

对应本平台的讨论和答疑QQ群：大数据和人工智能躺过的坑（总群）（161156071）