HDU 3976 Electric resistance （高斯消元法）

Electric resistance

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 326    Accepted Submission(s): 156

Problem Description

Now give you a circuit who has n nodes (marked from 1 to n) , please tell abcdxyzk the equivalent resistance of the circuit between node 1 and node n. You may assume that the circuit is connected. The equivalent resistance of the circuit between 1 and n is that, if you only consider node 1 as positive pole and node n as cathode , all the circuit could be regard as one resistance . (It's important to analyse complicated circuit ) At most one resistance will between any two nodes.

 

Input

In the first line has one integer T indicates the number of test cases. (T <= 100)

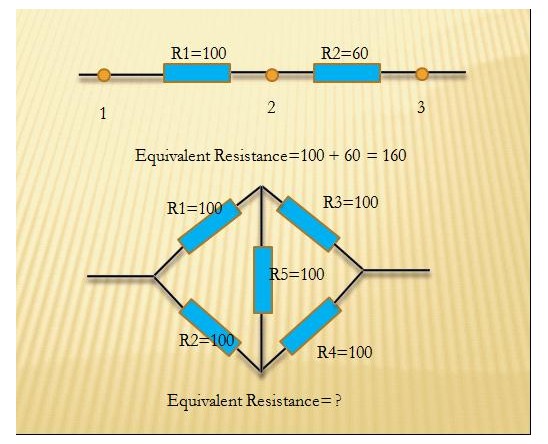
Each test first line contain two number n m(1<n<=50,0<m<=2000), n is the number of nodes, m is the number of resistances.Then follow m lines ,each line contains three integers a b c, which means there is one resistance between node a and node b whose resistance is c. (1 <= a,b<= n, 1<=c<=10^4) You may assume that any two nodes are connected!

 

Output

for each test output one line, print "Case #idx: " first where idx is the case number start from 1, the the equivalent resistance of the circuit between 1 and n. Please output the answer for 2 digital after the decimal point .

 

Sample Input

1
4 5
1 2 1
2 4 4
1 3 8
3 4 19
2 3 12

 

Sample Output

Case #1: 4.21

 

Author

abcdxyzk

 

Source

2011 Multi-University Training Contest 14 - Host by FZU

 

高斯消元解方程组。

主要是方程的建立。

我建方程使用了n个未知数，表示n个点的电势。

需要列n个方程。

就根据n个点，流入电流等于流出电流，或者说每个点电流之和（假如流入为正，流出为负，反之也可）

这样可以列出n个方程，根据n个点电流和为0.

而且可以假设1这个点流入电流为-1, 这样设点电势为0，那么可以知道n这个点的电势就等于等效电阻了、。

流入肯定等于流出的，上面列的方程组中第n个的是多余的，可以去掉，替换成1点电压为0.

这样方程组正确建立。

对于u  ---->  v  电阻为w.   可以知道u加一个电流  xv/w - xu/w.  而v加一个电流 xu/w - xv/w;

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013-11-17 23:18:47
 File Name     :E:\2013ACM\比赛练习\2013-11-17\EE.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;
 const double eps = 1e-;
 const int MAXN = ;
 double a[MAXN][MAXN],x[MAXN];
 int equ,var;
 int Gauss()
 {
     int i,j,k,col,max_r;
     for(k = ,col = ;k < equ && col < var;k++,col++)
     {
         max_r = k;
         for(i = k+;i < equ;i++)
             if(fabs(a[i][col]) > fabs(a[max_r][col]))
                 max_r = i;
         if(fabs(a[max_r][col]) < eps)return ;
         if(k != max_r)
         {
             for(j = col;j < var;j++)
                 swap(a[k][j],a[max_r][j]);
             swap(x[k],x[max_r]);
         }
         x[k]/=a[k][col];
         for(j = col+;j < var;j++)a[k][j]/=a[k][col];
         a[k][col] = ;
         for(int i = ;i < equ;i++)
             if(i != k)
             {
                 x[i] -=  x[k]*a[i][k];
                 for(j = col+;j < var;j++)a[i][j] -= a[k][j]*a[i][col];
                 a[i][col] = ;
             }
     }
     return ;
 }
 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int n,m;
     int T;
     int iCase = ;
     scanf("%d",&T);
     while(T--)
     {
         iCase++;
         scanf("%d%d",&n,&m);
         equ = var = n;
         memset(a,,sizeof(a));
         int u,v,w;
         for(int i = ;i < m;i++)
         {
             scanf("%d%d%d",&u,&v,&w);
             a[u-][v-] += 1.0/w;
             a[u-][u-] += -1.0/w;
             a[v-][u-] += 1.0/w;
             a[v-][v-] += -1.0/w;
         }
         for(int i = ;i < n-;i++)
             x[i] = ;
         x[] = ;
         for(int i = ;i < n;i++)
             a[n-][i] = ;
         x[n-] = ;
         a[n-][] = ;
         Gauss();
         printf("Case #%d: %.2lf\n",iCase,x[n-]);
     }
     return ;
 }

第一次写的时候用n+m个未知数做的，也可以A掉，但是有m个变量多余了。