Java实现线性阈值模型(Linear Threshold Model)

影响力传播的线性阈值模型：

网络中连接任意两个节点u,v之间的边都有权重，任意一个节点它的各个邻居节点的边的权重之和为1，即

N(v):neighbors of v.

网络中的节点分为已激活节点和未激活节点，每个节点都有一个自己的激活阈值Θ(每个节点的激活阈值可以不同，且现实情况下社交网络的各个用户的激活阈值一般不相同，有的用户活跃，阈值低，容易受人影响，而有的用户较沉默，阈值高)。未被激活的节点v受所有与之相邻且已被激活的节点u的影响。当未激活节点v与所有已被激活的邻居节点的边的权重之和达到或超过激活阈值Θ时，节点v就会被激活。

即当满足条件：

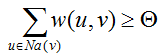
Na(v):active neighbors of v.

v被激活之后，它也会以同样的方式影响它自己的未被激活的邻居节点。这样会有越来越多的，满足激活条件的节点被激活，直到最后再也没有新的节点被激活了，激活过程才会停止。

上述过程被称为影响力传播的线性阈值模型(Linear Threshold Model)，传播过程停止时最终被激活的节点的数量被称为影响力的传播范围(Influence Spread)。

无向无权图的线性阈值模型的Java实现：

public int beginDiffusionProcess(ArrayList<Node> graph,ArrayList<Integer> activeNodeIds,int lastInfSpread)
    {
        //Mark the active neighbors of each node.
        for(Node nd:graph)
        {
            for(Node n:nd.neighbors)
            {
                if(activeNodeIds.contains(n.nodeId))
                {
                    n.setActive(true);
                }
            }
        }

        //Determine whether each node is activated or not.
        for(Node nd:graph)
        {
            int activeNeighbor_Num=0;
            for(Node n:nd.neighbors)
            {
                if(n.isActive())
                {
                    activeNeighbor_Num++;
                }
            }
            if (activeNeighbor_Num/(nd.neighbors.size()*1.0)>=nd.getThreshold())//如果是带权图，这里要修改
            {
                nd.setActive(true);
                activeNodeIds.add(nd.nodeId);
            }
        }
        //Get the influence spread of the current step.
        int infSpread=0;
        for(Node n:graph)
        {
            if(n.isActive())
            {
                infSpread++;
            }
        }
        //If it converges,stop the diffusion process,else continue the next step.
        if(lastInfSpread==infSpread)
            return infSpread;
        else
            return beginDiffusionProcess(graph,activeNodeIds,infSpread);
    }

下面的代码调用上述方法，获取最终的Influence Spread：

public int GetInfSpread(ArrayList<Node> graph)
    {
        ArrayList<Integer> activeNodeIds=new ArrayList<Integer>();
　　　　　//this.dimensions是已经被激活的种子节点，是某一个类的静态属性，类型为ArrayList<Node>，这些节点会尝试激活它们的邻居节点。
        for(Node n:this.dimensions)
        {
            activeNodeIds.add(n.nodeId);
        }
        int lastInfSpread=0;
        return beginDiffusionProcess(graph, activeNodeIds,lastInfSpread);
    }

其他相关的代码：

Node.java

import java.util.ArrayList;

public class Node implements Comparable<Node>
{
    public int nodeId;
    public ArrayList<Node> neighbors = new ArrayList<Node>();
    private boolean b_isActive = false;
    private double threshold = 0.0;

    public Node(int nodeId, double threshold)
    {
        this.nodeId = nodeId;
        this.threshold = threshold;
    }

    public int neighbors_num()
    {
        return this.neighbors.size();
    }

    public void setActive(boolean isActive)
    {
        this.b_isActive = isActive;
    }

    public boolean isActive(){
        return this.b_isActive;
    }
    public double getThreshold(){
        return this.threshold;
    }
    // Sort nodes by (out)degree
    public int compareTo(Node anotherNode)
    {
        if (this.neighbors != null && anotherNode.neighbors != null)
        {
            // reverse order
            return anotherNode.neighbors_num() - this.neighbors_num();
            // positive order
            // return this.neighbors_num()-anotherNode.neighbors_num();
        }
        return 0;
    }
}