Bzoj3677:树形DP

首先我们知道这棵树的形态，一眼DP。
考虑蓝线的性质，显然蓝线在树上是连接连续三个节点的。
这样就有三种情况:连接 一个节点 的 某个孩子->本身->父亲 或者 一个孩子->本身->另一个孩子。
然后胡乱写一个DP，发现并不能过大样例。
因为这种想法定义是有反例的!
考虑下面的这棵树的连边方式，怎样生成连边方式是这样的一棵树？

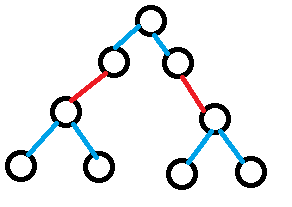
显然是不可能做到的，因为下面的两个叶子中需要有两个根才行，然而我们只能有一个根。
也就是说，确定了根以后，我们的连边方式就只剩下了 一个节点 的 某个孩子->本身->父亲 这一种。
(显然只有使用且仅使用这一种方式能生成可行的树)。
我们令f[i][0/1]表示考虑节点i及节点i的子树，i是否为蓝边的中点，能获得的最大价值。
显然我们有:
f[i][0] = sigma( j : son[i] ) max( f[j][0] , f[j][1] + edge[i->j] ) ,
f[i][1] = sigma( j : son[i] ) max( f[i][0] - max( f[j][0] , f[j][1] + edge[i->j] ) + f[j][0] + edge[i->j] )。
这样我们就能枚举根然后O(n^2)暴力DP了。
仔细观察这个转移方程，显然我们可以换根。
我们设g[i][j][0/1]表示节点i不考虑孩子j的f[i][0/1]。
我们有:
g[i][j][0] = sigma( t : son[i] && t != j ) max( f[t][0] , f[t][1] + edge[i->t] ) ,
g[i][j][1] = sigma( t : son[i] && t != j ) max( g[i][j][0] - max( f[t][0] , f[t][1] + edge[i->t] ) + f[t][0] + edge[i->t] )。
显然有:
g[i][j][0] = f[i][0] -  max( f[j][0] , f[j][1] + edge[i->j] )。
对于g[i][j][1]，我们可以把后面的那一堆东西提出来，那是一个仅与变量t相关的表达式。我们维护这个表达式的前缀max和后缀max就好了。
换根的话，我们就把某个节点的父亲的g[i][j][0/1]当做j的一个孩子去处理就行了。

代码:

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 using namespace std;
 const int maxn=2e5+1e2;
 const int inf=0x3f3f3f3f;

 int s[maxn],t[maxn<<],nxt[maxn<<],l[maxn<<];
 vector<int> son[maxn],pef[maxn],suf[maxn],len[maxn];
 int f[maxn][],ans;

 inline void addedge(int from,int to,int len) {
     static int cnt = ;
     t[++cnt] = to , l[cnt] = len ,
     nxt[cnt] = s[from] , s[from] = cnt;
 }
 inline void dfs1(int pos,int fa) {
     f[pos][] =  , f[pos][] = -inf;
     for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) son[pos].push_back(t[at]) , len[pos].push_back(l[at]);
     for(unsigned i=;i<son[pos].size();i++) {
         dfs1(son[pos][i],pos) , f[pos][] += max( f[son[pos][i]][] , f[son[pos][i]][] + len[pos][i] );
         pef[pos].push_back(f[son[pos][i]][]-max(f[son[pos][i]][],f[son[pos][i]][]+len[pos][i])+len[pos][i]) ,
         suf[pos].push_back(f[son[pos][i]][]-max(f[son[pos][i]][],f[son[pos][i]][]+len[pos][i])+len[pos][i]) ;
     }
     for(unsigned i=;i<son[pos].size();i++) f[pos][] = max( f[pos][] , f[pos][] + pef[pos][i] );
     for(unsigned i=;i<son[pos].size();i++) pef[pos][i] = max( pef[pos][i] , pef[pos][i-] );
     for(int i=(signed)son[pos].size()-;i>=;i--) suf[pos][i] = max( suf[pos][i] , suf[pos][i+] );
 }
 inline void dfs2(int pos,int ffa0,int ffa1,int lfa) {
     f[pos][] += max( ffa0 , ffa1 + lfa ) , f[pos][] += max( ffa0 , ffa1 + lfa ) , f[pos][] = max( f[pos][] , f[pos][] + ffa0 - max( ffa0 , ffa1 + lfa ) + lfa );
     ans = max( ans , f[pos][] );
     for(unsigned i=;i<son[pos].size();i++) {
         int fnow0 = f[pos][] - max( f[son[pos][i]][] , f[son[pos][i]][] + len[pos][i] );
         int delta = ffa0 - max( ffa0 , ffa1 + lfa ) + lfa;
         if( i !=  ) delta = max( delta , pef[pos][i-] );
         if( i != son[pos].size() -  ) delta = max( delta , suf[pos][i+] );
         dfs2(son[pos][i],fnow0,fnow0+delta,len[pos][i]);
     }
 }

 int main() {
     static int n;
     scanf("%d",&n);
     for(int i=,a,b,l;i<n;i++) scanf("%d%d%d",&a,&b,&l) , addedge(a,b,l) , addedge(b,a,l);
     dfs1(,-) , dfs2(,,-inf,-inf) , printf("%d\n",ans);
     return ;
 }

(换回了U2417H的我压行更加肆无忌惮了)