DeepLearning.ai-Week1-Convolution+model+-+Application

1.0 - TensorFlow model

　　导入相关依赖包。

import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *

　　初始化全局变量。

%matplotlib inline
np.random.seed(1)

　　导入数据集。

# Loading the data (signs)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

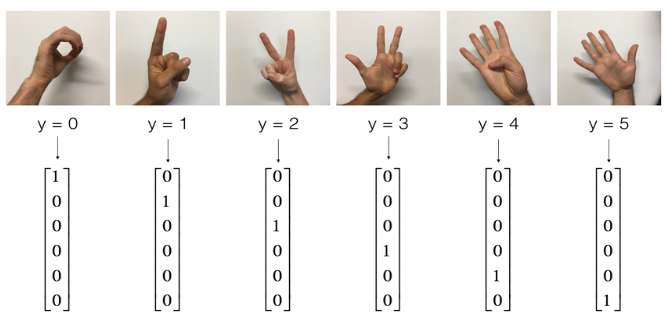
　　输出一张样例图片预览。

# Example of a picture
index = 6
plt.imshow(X_train_orig[index])
print("y = " + str(np.squeeze(Y_train_orig[:, index])))

  Result:

  y = 2

 

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAP4AAAD8CAYAAABXXhlaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJztfWuQXEeV5nfq0dUvtbr1tCzJtmzLbywZy8bGYIwfrHkEno2A2QFiwrvhCP9hN5jY2RhgN2JjZmM3Av4M7I8NIhwLi38wA4YBbLwsYPzgYeOHjN9vWZYluWW1pO5Wv7u6q3J/VPXNc/JWZmdVd1cZ7vkiOjpvZd7MrHtv1j0nzznfIWMMFApFtpDr9AQUCkX7oQtfocggdOErFBmELnyFIoPQha9QZBC68BWKDEIXvkKRQaxo4RPRrUT0GhEdIKKvrNakFArF2oJadeAhojyA1wHcAuAogKcAfM4Y8/LqTU+hUKwFCis492oAB4wxBwGAiL4P4DYA3oW/YcOQ2bl9e+2AVjDyqmLlE6FAF6mf1VZ+Z1fhWjXXRTtvTvMXJHjGmjuirsEAq9ClqXdy9J1hjI6OLXsDV7LwtwM4wo6PAvhA6ISd27fjF/fdUztwp0axWgc1LKYOU1+98bWg0KqNnEe6C/uBe0/DAhav5N/THcB468jXRWqs0HX0XJPQpWr54TUNiwBgyNfMbciKphoYiTcMXNPAFMPtqv5WgRsfL3V7Lgjr4xO3/WVUTyvR8Rs9BqlvQER3EtF+Itp/anR0BcMpFIrVwkre+EcB7GTHOwAMu42MMXcBuAsA9rzvMv6q8nbs/nqQtzZQE/gR5S9J98eWxNs61Eno7RGo8r2SQ/2kJsm/QLipbyhxGL7g/nbRiLxngZdwq3tRsS/rToJLnfJ7NiGNNim4ruSN/xSA3US0i4i6APwVgPtW0J9CoWgTWn7jG2MWiejfA/glgDyA7xhjXlq1mSkUijXDSkR9GGN+DuDnqzQXhULRJqxo4a8mQjpc9J5ncIfesFJofyGuXXBS/s1Xoci6u+dy7NZ0PX4JYjfh06p15EZBEL4+mrjP3r0GZ0dbnONaOdg1DeyNhG+a777IpsHrHeo++lqRp2yPvBYZB+qyq1BkELrwFYoMos2ivokSI2Ol6HT3HrGuwTxaGyHaOyaqCxOwOVLk9Uh333iO6SlGqjSec9J9uvbCxjbTpixqUoa3H6d0E94wNEJYwfF2IcR0913p+27OtTL8frotQ85gvJ09L/3oGOd/GPrGVygyCF34CkUGoQtfocgg2m7OWzLbhUxZKQgrTGv6aFjfXRnSbr9+/Tlo1Ykez29DamVvwDWl+q6Pay6VKrgbNLJ8f6l5RHxS69tvUgvr563deTmc39QX7GM13MQj7m3s+tA3vkKRQejCVygyiLaL+kuCSFqkCXnTeWLpg/HbjogtRK1ArHswCsyjLrhdRB6l1Z3lx00hFLkXCUrZhhqbKoN3LCW+NkZTceqR7VrT3QLqQqr7kCjuqTP+exukVxDv4tgnqXnoG1+hyCB04SsUGUQHdvU9n4fiJzweXGHKqEgxOnJH2+1Fkn6EWC5iemtUFyu/BlSVwE4yr8sFWDqCu/MhfUdMKbYT19uN14R2tCOVpMjrEXoAwwJ2wJuTey8GO/FTh/FFkg7GWbKWxUHf+ApFBqELX6HIIHThKxQZRFt1fIOQrs3KrbrWRQZfBbtoIeguRM6QIoYITqkFss3UXBofhGMOQya1wIxbuN5h/dbdawhEzEUi2iQYRGhzoOkeGuzfrMw0lx5heegbX6HIIHThKxQZRPvNeRFijQlkOZG0aU14tDFQyAzFCRNas9IF5xHkffNHx4S69CJ2qNhphFSTlEkzWncLfJkovTDcRYhfw9+Ha+JtwdMzxAsYHLrVYDIV9RUKxTLQha9QZBC68BWKDKL9On61rtG4ulKAeNKnF1NIc4o1ebmnBZRCP4FnE/ptwF5IwrU1jlDDJez0EXEE+SmD1qU4m2CaQNI3WDNofN+D5tM1gIncKIjN7xezz7V8H8197mLZNz4RfYeIRojoRfbZBiJ6gIjeqP8fihxPoVC8BxAj6n8XwK3OZ18B8KAxZjeAB+vHCoXiTwTLivrGmN8S0TnOx7cBuKFevhvAIwC+HDfk8maHUHSetBq5ffn79pNGBMxtqXn4BKkW7X4pk4/PlBMSo50uhenTry6ESDRC1CGxWBXp29vJyj3f0mK5P7JTtlr5NwsTsIQiDWO5+ZZHq5t7W40xxwCg/n/LimahUCjaijXf1SeiO4loPxHtHx0dW+vhFApFBFrd1T9ORNuMMceIaBuAEV9DY8xdAO4CgMvfd6mxokws31xA2ExJa3E78kGB1bOz7p4p5xQKXmlVJLPnVYN8c4EgINNY7Je9N+qTF+PeDeFvGWlCaCaAx1eV4rpr3Gk836FEyptzNXSaFqwBK1V2Wn3j3wfg9nr5dgD3ttiPQqHoAGLMef8M4A8ALiSio0R0B4CvAbiFiN4AcEv9WKFQ/IkgZlf/c56qm1Z5LgqFok1ou+eeRUoJt+WA3hrSZlwfNnEUnULb36PUVJm+X1kU7arzs0k5V+qW8yh0RY0nUye3th8iPndJRYUeH+flGLpqYZ0z9syQYYvvBYRMXnG9N6UTi4sQ66UZeE6jPRnjzadL+0xKtqlQKLzQha9QZBDtFfWNQdXUeMNTZiJBa+Zwi5NtKyx2IdOKGxvjzMPXME5YA6rluaR86unfiLrK8SNJOT+4WdSt33NtUi5t2Co79RFnNMVVwU0+IZ53P+GIf/BVYCZZhZRfwe6DlaG7G/k9o70cVwPhcLKVQN/4CkUGoQtfocggdOErFBlEB3n1/ea8tO7e+Ky02urnP48m6fSHAooBRw8dSMpHHv+9aNbfVUrKhRMyPmF6/HRS3nbTp0Vd18Bgw2mE1bk4t+Jm3Jt9ewOu+2uaYLMxwkQWccbJaAtYZMOwUc7R3FfFLTe2MvaaSjTrOqxvfIUig9CFr1BkEO333FuSm1LeaAFx0EO+kRY9+UGIi56rDi4RBx/J7/03eXo8KZ8YOy3alXv6knJ/r6hC4fi7SXn4iYdF3Y7rP56U88zjLyhSR4dpBcTXFP9h44apiLaQfOm5nalvItpFy/PyqBU1wJ278T9X8XOJNRe6aHx/g2d4zIqxM9c3vkKRQejCVygyiA6k0HILDUCuKMcJJfhvlT94JT5pU2si3/od5yTluS5Hnp+1QTqgvKjqZ9NffPNVUTcyuCEpn3Hlh9iUZB9i071F8go38IfDR/jQ1Ia8r+8gz3fgvHh53jn2BDs1Nfe4nfaAUQnLXMmmEVRzI6BvfIUig9CFr1BkELrwFYoMogPmvPq/SFNQuNIxtwW80XxRYGkvvsb6rdt2YIuNrNu292rR7s2HfmH7qMqJFPK2jz5nb2D0hSeTcvcm2//Qrov8cw4zh7JygMwjlkCyGSYO32jB296q7hvw8PM9E27qsZY9AxufGL/H5G8bnlIcqagP+sZXKDIIXfgKRQbROc69WHnHPY2TdCwuiLrqYtl2VyyJujw/DpI/xKWd4mbFC679sGj3zmtJflFMHjsq+2A/tVXHSpdfsLfj8KMPJOXuDTJRUc/6jY0mXpuzR7qP1gicw1DwijCVpfqIFD1biYBphgzDZ54NsI+EOAjTsG2r4tN4z73WFBz3W6uor1AoloEufIUig9CFr1BkEB1z2U1HacXpQOXTp5Ly6NOPynYTNmKu0D8o6vp2X2rLZ+9OylQsBufrmyI3R/YNDYl2l3/sU0n5D//0HVE3PzmRlCfn5kTd0Cbbz/ou+12G9z8i2p39oU8k5XypJzDhxvMF4qkag2QesX0Ik1oTmzstu+nyLnzmthT7COvNv4mQ3hlYuftttDNv6DKutssuEe0kooeJ6BUieomIvlT/fAMRPUBEb9T/Dy3Xl0KheG8gRtRfBPC3xpiLAVwD4ItEdAmArwB40BizG8CD9WOFQvEngJjceccAHKuXJ4noFQDbAdwG4IZ6s7sBPALgy8v25xf2/edUK0n56FN/SMpjzz0t2pXyNj1VrnBc1L375ptJeejyK5LymVdJU1yh24rOaSmxyur8stX2Cy9OyhfceKuo23/fD5PyAElzZD9LxWWqdqypt14W7d7p6bdjXXWDqMs7ZkzbYfAwDgEWjZZF1MiZ+NJ/L4/GbVOScpWZJt2xiX/P1c0D0Ggu/gq/B2QwlXoDNLW5R0TnALgCwBMAttZ/FJZ+HLb4z1QoFO8lRC98IuoH8C8A/sYYM7Fce3benUS0n4j2j46NLX+CQqFYc0QtfCIqorbov2eM+XH94+NEtK1evw3ASKNzjTF3GWP2GWP2bRjS/T+F4r2AZXV8qtGWfBvAK8aYf2RV9wG4HcDX6v/vjRnQEla65hS/7lRl+u7xd63ufvr0jGjXV7I6MuXmRV2+y+r/5Wf3J+U5ZgIEgG37PpiUezf5tRehZ6aUQuuLe+l1HxFVYyPHkvKxZx4XdXPz1uV4Zs7Ovwcytfap5+V5HNuv+mhSzjNTZdqI1ryu2jq//BqTaAb2GiQBK4/ik99fvgHj5+F7bFNpyf1dOCPHRa2m1X8j/y+DGDv+dQD+GsALRPRs/bP/jNqCv4eI7gBwGMBno0ZUKBQdR8yu/u/h/8G6aXWno1Ao2oEOeO7VfkNS0nEgcCqXt9McPM+SUrz5woui3SITc3pK0qzVtWDVgELZlifffE20mz5ho+nO/MANom4DGxsB4kZO6lhwPAOvvPmTSfmh4cOibuqUVWNyk1b4rDpkHr1Fez1Gnpbpu6hkOf13vP+DrMJP3JDiy48kzliNDNchlcnn0RagxA+bLY3fZNcqF2ZI45PzCBDIRI8WkV8hsjP11VcoMghd+ApFBtG5FFoBDri0pGXbnvf+q5Ly5IRMXfX8A5brbt289Iob7LP8dpSzv3d5kjvm1dPWReHt3/0/UTc7Zeu2Xmy9//JdTqAPJwtx0D9kSTQuu/Hjou6xe75ru5ix3Py5nLxNBWY1yJMc6/DjDyXlns3bkvLGned655TiPxSedkwlSKkLfniycDVo6Cej96kcLTr/BU8R39PlrI8mG4y+Iv65tGw5aU7W1ze+QpFB6MJXKDIIXfgKRQbRVh3fGBtFRHD14Jxo50O+YPXpvTfcLOqqzOz3+L0/FXVTc9ZDb6jPesgN9Ekii75+m57aVKVn4MHf/jIpj71zKCnvvFJG+PVt2JyUKScZNSlnv/eOCy4Vddsv25eUD+1/zJ5Tdcw/FdtHb480W5bn7fd8/fd2vlf+69tFu65uxumf0q15vjn4Eedk5s3Flxo6lqMjNhQwgJDeHu7B0f+9F6hVW2eIkGblpB9L0De+QpFB6MJXKDKINpvzTEIwYVK/OVXeyjnLA0fMuvyDLLW0I2o98bP7kvL0SRsevG56SrQbmLOif7EgxfSefls3+fYbSfm1E8Oi3ZZLrci+6fzLRF2x15Jo5HPSDHjZh60H9OFXrFfi2OgJ0a6Qs1ek0CVvYU+vFeEnjx5MykdflKQlu668jh35OeZblVijTXGx+sIyo/nO8XWRSjMd239IV2kxDXeagz/ddWBGLUHf+ApFBqELX6HIIHThKxQZRHt1fANUl0xRjq4kOOtTRAicaIETXvpdYy+75gPiuH/9QFJ+9H6r7x89/LZoV5iYTMrrHFPfNmaaKxTspSvMSbPfu/sfTsqjh14VdVved01S3rDzfFE3sNG681587fVJef99PxDtZsrMHGkqoo5ful62R3HkiYdEs8FtO5Py0JlnwwepZ7ZGcunL59dUl+IZiBq2NlykR62oCpCKkgm5LQcIQUQ55LLr2TNIN3TqmiPi0De+QpFB6MJXKDKI9nruwaDqFc9ZumGnDeeYN0KEdMRc+MWkXRdbrvuN22zU2tOPyjRcT/7apqcuz0rePhqzXnGLFRv9N7SuV7TrLlkz3eyINPW9/usfJ+Wh898n53iV5ee74Eqrqgy/+pxoN33MEnhMTEs1g185TkZCc9JseeD3NvLw8k99QdSVetdhpfBJnK1K+tF9hDJyBchHwpMKpE73dBM2Dwb0XESaBB2Vo1pvHHs99Y2vUGQQuvAVigyi/Zx7S/xxLvkDeQ+8ZA0uRbLDICFr2HjrBtcn5etvlWQY23buSMq/+b/3ibpTJywn3iJTP+YYnx8ArGOBPn3d3ZCw6smR/b8TNWOMg+/CD9t57bn5U6Ld4z+6OynPlqU6wkX9csWOVXK8EOcPWc/Dg48/LOouuN6OnS/wRyQkZMe5+LVK0R09UirgyNdfE2Qb1LDYqNOoPmJjkYJeiO4SafK66htfocggdOErFBmELnyFIoPoAK9+Yw+jcKwUV5Dsb1XYsckxCfK9Aaafu7rdBZfZaLoh5kkHAL/5+c+S8uFXX0rKM3Nl0a530prYBvqkqa+325J79nVJos8y4/T/471Wjz9zzwdFu7P2WMLRA3/4jahbrFqdf4ERdswX5K0uFa3Of9jZa+jqs9z857zfkozki3K+0goV2LOJ1D9j0183FeEX2UmKcNTbNm4vINRH0BzZ4rVq9gos+8Ynom4iepKIniOil4joH+qf7yKiJ4joDSL6AZFDV6tQKN6ziBH15wHcaIzZA2AvgFuJ6BoAXwfwDWPMbgBjAO5Yu2kqFIrVREzuPANgye2rWP8zAG4E8Pn653cD+HsA31q+v6Tk+bwBtxix36eQ2Y+Z91wiDsPSUJkA0RtXHzadcYao+/i/+XxSfuq31gT2x9/8VrSbHLOBPlNTs6Juy5D1ilt3xiZR11Oyg8+wwJ/DTz0i2i30bEjK5bwk86guzNlyxX63+ZzMM1DtsQFIfQXpAXnoMcvVZyrWVLnr6htFO57aLIVVEe99Rjz/s+NCPAXBaKG4WQT7bxmNU3ulg9UCXTRpJ43a3COifD1T7giABwC8CWDcGLP0VBwFsL2pkRUKRccQtfCNMRVjzF4AOwBcDeDiRs0anUtEdxLRfiLaPzY23qiJQqFoM5oy5xljxgE8AuAaAINEtCTr7QAw7DnnLmPMPmPMvqGhwZXMVaFQrBKW1fGJaDOABWPMOBH1ALgZtY29hwF8BsD3AdwO4N7l+jKGpXwOBUel7HQsqorXkfu7RZ4yhPIu9P9UJCAfS9Z1M734Qzd/LCmfsX2HaPfQj20E3typEdk/c6qdn58TdfmcNYwU89xIInXwuXHb59iJUVG3a/uWpLx5gzVHLi5Kt2L+zbqcVN5gkYeHGIFHz9BW0WzbhZcn5TBPfZBtE77KlkhAQmaugPlRHsYnE4il7OTkG66nOfkuj3F7J19V0+a8GDv+NgB3E1EeNQnhHmPM/UT0MoDvE9F/B/AMgG83ObZCoegQYnb1nwdwRYPPD6Km7ysUij8xtN9zzyuTBDjVmCxkuOdewMMvldrIE2GVno/9IE0awjz+WKrt8y+RqbC6WUTeEz+XEX7zo+8m5bGJCVE3NWNF7hxXTZx5sKFx1la5b1JinPtnbLAeeHkn1fbohCXmmF2Q/ReLlsBjbsaaJl/77S9Eu4EtZyblviFpmoxFyJznTRnVhFxLHq4+99mR5mR5PURb57mS5kJfhfwgGEkX4haMNVtGQH31FYoMQhe+QpFBtD+FViK2ujTFgagOvg0qdtodsYsCoj6jxs4xdcEV64RYnWIw9nj/Oe227zo3Kd/y+b8WdS89ZoNq3nr2j6KuPHE6KVdYgA2qcoCzd9jd+rN2Su/Cd989mZTHx63fRE+XJATpZam3JidPizqedThHtlx2LBSHn/lDUr7ohk+KOq4KtRpOQp5nIkhkEbnb7aoYfKwwH5/rVcqtRcwilJqHn82DPDpCc/yEzQn7+sZXKDIIXfgKRQahC1+hyCA6YM6r1P87vzlCnQt4QHGdKqXH8z5l/0L/5x5QOdesw/n9nf6r/LjC2rlmP1vXP7hB1Oz7mCXOPOOc80Td07+0XPeTIzY19sahftEux+Zx6sSYqONbA+OMEGS2IKPzSoxUo8sh6RiftKa+/n47djEvr8fI688n5e2X7RN1A1ts7gKpqbfGrC8yS6Uq/eeJey149ePRSgReNKHmsmeyPqLWSNxI+sZXKDIIXfgKRQbR3hRaxqCacL076a9CIrxoxjz3co44Lyx9Lq8+N/X5efuImf0cS58Q6YVKUJEBMLPjp5JyeUqGIi/OM2KOeZnWaucuG+xTOsNm9x0akKL+yDFrVhseOSnqCsxrcIalAOsqSGY0qtrrv3nLFlHHv/ZpJvYPDQ6IdpVZW/fWH2Uqsstu+YuknMtJTn+OIBGHJ8KmRWr+ZRAIJAo8j3z+kiMmlPMhwCnpO2eVoW98hSKD0IWvUGQQuvAVigyiveY8YxJ9OB09509FLPQlobvLllVWl9L/BfkG1xfd0Rrz79eOrS5fZmSYB5+Q3PZzxw4m5UJVcu4vLlizGjkRc0O9loN/kUXZrRuQ3PyL5aGkfOTYKVE3OmL3FKrse67r7xPtKiyvHnWVRF2Z7Vn091ryEXLINYnt0xx77XlRt3OPTfM9dIYkKvEi5ebK9eKAKS6gg6+KmhwksuR7U+zTVO7GRmc0GCpqJHijBGPNhvrGVygyCF34CkUG0XbPvWpdXHZFcZ4aK539mpnimAjsUOJJx71URqc8q6o2LNc+YHWOqE/Girbjx99JysOvPCvabR6wJrV1vVKMPj1uefbmZqUZcGDAcu6PnZxOyj3jkrCjq8sSdvT19Yi6ExP2vKlZnk5LXpCukjXvnXT67x+wfa4ftKbEhXl/Su55xzT5zmsvJOVBRtiRjsqM5dX3fxqbIlqQcoQINaJmsXSeh30j4LoX69WX/jzCozVS1tc3vkKRQejCVygyiPZ67sFYT6dUYAuHny8vRJEcEsqkSNl4t7h2yI+dOTLxcGrcBsdUq1JkL+Tt72nRoa5eWLT9lx2Cjfmy3fHnqbfW9Usabq4ilB3a7E2b7I7/zLD18Juak2J6LwtOmpuQATwD69lOvsgyLL0t8+y75Zxgp2MHbDbh3Vd/JCl3laRqEhSxje/Gp1rG9egzDrl1gZFSXfosCqlHOEQ/zvsLjBUS9dcihZZCofjzgi58hSKD0IWvUGQQ7SfiSBXq4F53oYAtHmWXIsPk3bmdNN5TSEWHGb/+L3pjHnjFvIw+KzBii7zr7cYi1WacFFpvHT6elMsz1iw3Oy09906OMYKNeamfr1tvTYID66233pzTboExduSca5NjunV5hnke5h1vyJx/L2Nq1H6XyVOWVGTTmWeJdsbjUQmkqFTZOa254/Gzcs0p8p45tTi432nV4fAPTKlFQpMlRL/x66mynyGi++vHu4joCSJ6g4h+QERdy/WhUCjeG2hG1P8SgFfY8dcBfMMYsxvAGIA7VnNiCoVi7RAl6hPRDgCfBPA/APxHqtkwbgTw+XqTuwH8PYBvLdtZ3YxnAr85qWyiopK384vpVUdszBmPOS+VoZXz6vvrKouM5KIoL2ORHzv2mWLBivpT09LEduioFYm3b7QeczOOh9/UrFURXLGXZ8U9c6vl3z9xSnLnT0xbdaE7L8X09T3W87DA1IB8QXLzc+WBHHWnOmdVldHht5PyRkfUl/CLryZAuhfKquszjzXFiRdpLYxFsItIs2JTgUoNEPvG/yaAv4NVlDcCGDfGLD1lRwFsb2pkhULRMSy78InoUwBGjDFP848bNG24u0BEdxLRfiLaP+74hCsUis4gRtS/DsCniegTALoBDKAmAQwSUaH+1t8BYLjRycaYuwDcBQAXXXj+2pGIKRSKaCy78I0xXwXwVQAgohsA/CdjzBeI6IcAPgPg+wBuB3DvsqMZq6tRSj+PdGnkkXWBPGnkkmh4/H5ThAmCUFP2UWUuqwtz1qU275q5GJmn65lcYOa9xUVZOTNn+y+WrAlvoSr7r7Lv4nL6c7KQ7i5rzusqSh2cX/91fVJ33zxkTYLiNhWl4WaaXY9yWe5D8HmdeOetpHz+ldeJdjkKRWXyCXs+d5ByofWZZFvU1Vt/c3EikdjB49yPne6jsBIHni+jttF3ADWd/9sr6EuhULQRTTnwGGMeAfBIvXwQwNWrPyWFQrHWeM947nHRM5hmiRerbid+U5wv5TIFzHluNBrnqVtkpBTVihS3KwvsPMdUlmPebm5EW3+fFaVLJSt+T8xID79ZFsUHJ61VN+Ptm2Nmv4JDbc+H3rx+vagrsD4r7DpWIMV5TnxijJsnwZ53avhoUi7PzohmpV6ZM8AHXyqs1HGKgMWDoHeo20ecHB2MngueFwcKmvrWxpynUCj+jKALX6HIINou6vtEkpD3VawYI3fk/Vv+sjdnV5z1UQ2J+ky8n3cCYObmbWCLm4mWk22MT06LugU29rFR62k3P+dy3dl5bD9Tpr/i5BWLi3YeBceKMsBSbW126Ltn2Xlzi2znftER55m+UHHSiBG7VhOnbMDO6HFp9d12zm52kkuJbhEKzOEidrTA627+B5qGuF+i+fJ87qeQqi1vlnbGC3zP5ij39I2vUGQRuvAVigxCF75CkUF0QMdvDGGuCaVScmrEUYC7XKTNCuwF8LGqjrmwyrwBq2yw6RmHyJJ58nU5RBzcRNjjeMy9M2n7mThhyTxNRerWGxnBRqEgf7snJuzeQHeXras4JsdtmwaTcq4gNcMyG4/rnzlH6awwL8HFRbnPwVOHzzOz4gu/+7VoNzC0OSn3DQyKOl+6dC/BZa3WOfI8O+5DFhndlt594no330iK5+2PHSyOiDNuJH3jKxQZhC58hSKDaLuo7+PTk6QafluLCfCfBbnLhRrAvcDchrw/53eRrPsbdVkT2Nhp6Y1GPCOuI1IWirbP7etlBtsTU9aMdnLMhjDnHe+8vh7rDXh6dFTULTBTXKlkPfIqjrpQzDOPPCNNcX2M+55ft7myVBemZ9mx0z/3DMyxe3vswAui3QuPbU3Ke6//V6KOeyFK3jt/Gq6gl12T3PONxov14mu5/1Um/fBB3/gKRQahC1+hyCB04SsUGUQHovN8Sj4rB9wpgznC/EFaTshV6PeOmf3I1fHt8fptljRytionPD1n9exNjptrb5dNm929XqbQvq7bHi+qEdwsAAAS50lEQVRUrJnLvWYzzIV3elZG7uWLto+hAUbEsVFGwQ30Wj2+u8vh/qfGZinj7DUssOP5gCtrkYXxVdgeBAAcfObRpFwa2CDqLtq7Lyn3cH0fftfekF4c0s75c9UcZ71p2CoV9enjzgechBBx7sfpuqX9lrg9CH3jKxQZhC58hSKDaL/nXoQkkiZaaHyU6sqfjclRA0JeggFTHxP1N5xhRf2zz79QNNsJG3U32CPF+fkZK/rPLEhvtyIzFxZLLD2VI4oP9ts+y/Oy/wJrW2LlnMMLuMhUkPl5J/01byv4A/15DCoOf+BixTRqliItmZsYT8pP/uqnom589FRSvuLajyTlgUHp4ZdjacmCBBWhCFCu0rjc/P6znHat6RlGpI+Lm4d75JLGLAd94ysUGYQufIUig+jcrn4TDlYi4RXj1XM96wJcBzIJrvjcCcThopZbxym7mWh18bZNol1pwvaxUJVkdwtF2+fo9ClZN8fSWvWyW+MQ5hkWAONmywU7nmEBPOSI+jxQyQ16KbB0WFyMrjoXdW7ezmNmXnr/zTHewQoX+1Mch7Y8MfGuqHvmoZ8l5amTtm733g+IdjvOPT8p9/WvE3U8oy9RQI3j50RyPqZP9PNGCnUhUuwPjeXSqi/M1Dw9XfIYH/SNr1BkELrwFYoMQhe+QpFBtFXHNzAwS3qyo1f6dHC3LuimJfp0I7hYmavqzmD82CXi4GQW8yePJeXyiWOi3SwzlVVJkm1MLbA+SKakOj11Min3GXtr5tx0YIan8pI6fpmlyeZmOTfNV4574aUYHpgJj18P51qVmTlybFp6EHLrHs8fkCLzYFF9VcckSMaaRd9+7rGkfPTAK6LdWZfsTcoX7JE5XrafvSsp9/RY7z/KhZ6dANlrymIXGU4XYOzkBKl8HyXnPsPcfDoviVqnT9cITasVZ8/Hg6iFT0SHAEwCqABYNMbsI6INAH4A4BwAhwD8pTFmzNeHQqF476AZUf+jxpi9xpglB+qvAHjQGLMbwIP1Y4VC8SeAlYj6twG4oV6+G7Wcel8OnmGsaOemKTIi+5VrYvOYgwJedyFRn4vwrvhaYR8sOl5m3NtteswSYEyOSrNcdYH1n5Pi/CSTxKYXJFffzJQV38qwKkJxQZrK+LzKZUfUZ+J3kXH6d3U5JkEu6jo3g1+DhUXmVeaIx4tMTJ+ak8E3XHLuKjIPQqcPd/4cPN0YmAmzPD4i2r355CNJ+ejrL4m6M3dfmpQv3GODfnactUu06+mzAU05l98/MlpGEIIETNLpNF/cy5GnL3OyNbNrMD0un7nREzU1cdF5VnyIfeMbAL8ioqeJ6M76Z1uNMcdqkzXHAGzxnq1QKN5TiH3jX2eMGSaiLQAeIKJXYweo/1DcCQBbNm9aprVCoWgHot74xpjh+v8RAD9BLT32cSLaBgD1/yOec+8yxuwzxuwbXD+wOrNWKBQrwrJvfCLqA5AzxkzWyx8D8N8A3AfgdgBfq/+/d7m+jDGJXui6LVaYq6EbBcbNaFWR287RgQImQZ+ZLmWyY8cuFz3XrWfJEl6OLEj9efqk1b8Wq/IST5S5u60k6cwznvpp9t1KJdk/n/O8E+HHXWeLRTvHvMO/X+HXyjVpskpB9JmTfZSZPllxrmMv21PIs+8yV5YupfOsj4Kj/3cX2P4Im2RX3jUJslx/J98RdQfHTyTld9+0gurW8y4W7S5i+v/Zu84TdTxledqCHJc9LxRvGnI151go2+85OTUh6g4cPAQAmJ+Xey0+xIj6WwH8pP4FCwD+yRjzCyJ6CsA9RHQHgMMAPhs1okKh6DiWXfjGmIMA9jT4/BSAm9ZiUgqFYm3R/ui8ukhYccR0Luq7Ijb37hKeXilR32+m4+JxRYj6sl0lpAZwmbhoxb/1l10r271zOClPjEuRDMxkhxnpfTVXtt5vc4zrnmYcEw1XW/IyxXVunTVLLSzM2rLj6cW/mZv9mt8bEalG8mJx7aHfUUdyrHKBXcc5x9wkejR+tWuRlVOxczzS0BWVmcl0/uTRpHzk9AnR7OTbr9u6S64QdXuuvi4pD22QG9TC5Bjg/pfzTX0S1Y4/jlPOM/HGwbcBAHNlaSL2QX31FYoMQhe+QpFB6MJXKDKIDqTJrikqwSAnN3W1SHHd+HPAMQOm+li+v9REXNMNq+Kup32O3tcztDEpn5naQ7AfLLiuuMI8xsybFTlJzirT0yv58kssAm1mwpoVX3/md6Ld6HGr76ZYfBhrEHchdSPr8jmmgzsXa5a5+nJXU3c/YYHt2RRSqaXtvPqY229XUb6vCuzG5B2TYw8jHC0yJqNKVX7nhRNHkvLLv5MuKcOHDiTly676oKg7m7P/9Fk/lZwzDwg34Dj9332+F5jpdnbeidhMIj3j3uX6xlcoMghd+ApFBtH+NNl1KceN0soZRv7gmDfyaGzKqTi2G576qeqISdwSxYeuOD99khDETxYiIwbddn6SC9GHowZw86GYPTmmsry9bfmcU8eOe3utaW/dR/9CtHv7tWeT8uE3JLHF7Iz1KORTdFNtz87adrMLjgwvwy3Zx/JL9xTtfNf1FmUdMwl2MQJQh1ME3UyEL8rLIdQH8ci50aH8AVmcFXVjB19Oyo+OSNKV1xnRx/kXWm/ArdvOlHNkKlghLyM2Bae/uFbyGZ6atibZ0ZPDoq5SJ2Bx1QMf9I2vUGQQuvAVigyivaI+WVHUkXJRYLKXG/fAD6tsdzRv5O9WNbTjz3nNAh5+vJ1xxXTO1ec5p3bMys53CXH6VT0ehW7/VXZFFlMuinbnl3uP5Ys9otmFe+zu9O7LJE9dVWS0ZRyBc9L77+Xnn07KB159WdTNMTWAX7e8864plazYu75P8hP2d1vRn2/kF1LWFtOwDEjxXvB6uJqJUPHk09nFeAwXJiQBxpEXLdvc4TdsENC6QZn5d3CjtfS43P9FlkGZ8+JXHWvOxIT1Ah0elqL+qRO1eZXnpJrig77xFYoMQhe+QpFB6MJXKDKItur4BEp7NNUhaMcdHY6TH/JILDeXGwQ/uVPlMcWFdPw0535jUsR0FB/bJ3A7EZ6Bjo6fmnXjeXCvPpcQVEYvcjOo43XHbGKcsAMASl09rM4+Ij1960W7qz80lJS3nLFd1D3z5O+T8hgjI3UjL8em7X6C68m4qb+bla0eXOqV5jBuwXO9C8WTwDZOXFMqsxamTMH5HL/XcnOgxI7L06eT8ulpGZU5NmwjNqtuzkdqvCZSRDBsr6GyKK9Vrn7fSXPnKRQKH3ThKxQZRAeCdGpwf3EMF+dT6Y2syGPYmTlXimanpUR4DxGHG6XDRUBXaCSPupAS5oUq4ecFdMlIjMecF0rltehEvfBAH64GuKQlXPR31a8C94RjakCX4xbH+fi2bD9X1O27zormLz3zRFI+PnxEtKuyOU4vyO+5MGGJSaZYINHQbEm0W99jRf++knykiznuFce+c971eOTpxpzU5uyaUs6vWhVEajZXjWMqmPNM+NLHVR1VsMz7cOaxdDvdpeODvvEVigxCF75CkUHowlcoMog26/gmibyLVEWCbV13WGcoeSj0bj+hZmxevRBhp8906LZ19W5fn+k52so0MSmva2zaA6SOn5ojT8cs8vTJ94RIve3orYXuwaR83qWWs57y0nR44p1DrAu5X8HNtVz/r85I7vg5Fhk40C37X1eyx6Uij/BzSD/YPpJr+ix2sfwEzhwrLLyT5xlw3axD+fd8ruZVp48Si7w0VdddvXae6vgKhcILXfgKRQbRMc69tEMbM7sEEg7xOpdzgItJbkonX9qskKjvBEdJoozGPBO1doEoQZHlu0V1RKQUc8VjpgZw82AqWpGTmzhio+/LhebhOp8ZlmKs1Gs9/Hac9z7RjpvVxt99W9QRSynGRVjXv3G+yk2C0qON8xPympKTUowb8JwMXYLHz7H0CXSzlOixhBguRIo4R43LsdwFbt2SN6dLcOND1BufiAaJ6EdE9CoRvUJE1xLRBiJ6gIjeqP8fWr4nhULxXkCsqP8/AfzCGHMRaum0XgHwFQAPGmN2A3iwfqxQKP4EEJMtdwDA9QD+LQAYY8oAykR0G4Ab6s3uBvAIgC+H+jJIi4uiMim6tNlMfOU75giI86HddBMQgQPU27EU3eI4JelHji3UEb847xP5amUu9st5iHRPTmosQ4293cjlOGQicM7ZCc+xd0qBpRtbN7hZtNtx3p6G7QBg/Nib9oBlxHWkdLFjvuhc73l2fXLMClFd8KcDKzmkfuK+O89vkfEf8obkZsRlInjqWgnxvPGz7sJVZZeyDvuz90rEvPHPBXACwP8homeI6H/X02VvNcYcq03QHAOwJWpEhULRccQs/AKA9wP4ljHmCgDTaEKsJ6I7iWg/Ee0/fXqyxWkqFIrVRMzCPwrgqDFmKdLiR6j9EBwnom0AUP8/0uhkY8xdxph9xph969eva9REoVC0Gcvq+MaYd4noCBFdaIx5DcBNAF6u/90O4Gv1//cuO5oB03ldgkq/QhPtdRcwo/nqAta2lAeX0NtESmQJ/muaUq1ZF67ppVptrE+n5yHOkgN4Qr1MKiLMH50ne7ed5Nz3hOF7CI4nGSe5ZNeqUJAkGv0DlpRyx7nS1NfdY9ODjRy2RJblOSk5Cp0/9RixPQ92bXqK8tHnZBgLKZdQPv+8r0qYAXPOfgi/124qb66WEzMshtT1shOV2V1vHGvOi7Xj/wcA3yOiLgAHAfw71J7ve4joDgCHAXw2si+FQtFhRC18Y8yzAPY1qLppdaejUCjagbZ77vnpK3ibAMNGpCkuRHUnenYzwAq5y2/W4TwIsam2AGmGIccUx81qOcYyQuTyqHEvRxeNzXSViqMgCNOTrweJtBci5zh0RFuPp50rvuYL9hHs7R8QdWecfVFS7mZ1wwdfFO1mx08k5UVH9eHiPR+8kJfzzXPuf0ea57kcyK0U5C+2z4Lj/hcKaOJqGJFfrRB8gnmZ7be6WE2dH4L66isUGYQufIUig9CFr1BkEO2PzvOa7bgenzrJU/Z3nTYPNja/kUvIwH4LyTFzGZG3j4/l6s+87Oi+3IXUcZXlx9wc5PKu8+NUDgJOosn2BhZIRq1VA5dU7llIA6dsyPZb3DyD3rNcHZR9T+d6l0qW33/j1rPs5939ot3brz+TlCdGjoo6Ea0oSFvd6+HfH+oWJlg5xy72/BQYUUbO8SuWZjbnfvIadlB0dXxOHOrmZKTVd9lVKBR/ZtCFr1BkENQqYUBLgxGdAPA2gE0ATrZt4MZ4L8wB0Hm40HlINDuPs40xm5dr1NaFnwxKtN8Y08ghKFNz0HnoPDo1DxX1FYoMQhe+QpFBdGrh39WhcTneC3MAdB4udB4SazKPjuj4CoWis1BRX6HIINq68InoViJ6jYgOEFHbWHmJ6DtENEJEL7LP2k4PTkQ7iejhOkX5S0T0pU7MhYi6iehJInquPo9/qH++i4ieqM/jB3X+hTUHEeXrfI73d2oeRHSIiF4gomeJaH/9s048I22hsm/bwieiPID/BeDjAC4B8DkiuqRNw38XwK3OZ52gB18E8LfGmIsBXAPgi/Vr0O65zAO40RizB8BeALcS0TUAvg7gG/V5jAG4Y43nsYQvoUbZvoROzeOjxpi9zHzWiWekPVT2xpi2/AG4FsAv2fFXAXy1jeOfA+BFdvwagG318jYAr7VrLmwO9wK4pZNzAdAL4I8APoCao0ih0f1aw/F31B/mGwHcj5rreifmcQjAJueztt4XAAMA3kJ9720t59FOUX87gCPs+Gj9s06ho/TgRHQOgCsAPNGJudTF62dRI0l9AMCbAMaNMUvRK+26P98E8HewfB0bOzQPA+BXRPQ0Ed1Z/6zd96VtVPbtXPiNwoYyaVIgon4A/wLgb4wxE52YgzGmYozZi9ob92oAFzdqtpZzIKJPARgxxjzNP273POq4zhjzftRU0S8S0fVtGNPFiqjsm0E7F/5RADvZ8Q4Aw20c30UUPfhqg4iKqC367xljftzJuQCAMWYctSxI1wAYJKKlUO123J/rAHyaiA4B+D5q4v43OzAPGGOG6/9HAPwEtR/Ddt+XFVHZN4N2LvynAOyu79h2AfgrAPe1cXwX96FGCw7E0oOvEFQLlv42gFeMMf/YqbkQ0WYiGqyXewDcjNom0sMAPtOueRhjvmqM2WGMOQe15+EhY8wX2j0PIuojonVLZQAfA/Ai2nxfjDHvAjhCRBfWP1qisl/9eaz1pomzSfEJAK+jpk/+lzaO+88AjgFYQO1X9Q7UdMkHAbxR/7+hDfP4EGpi6/MAnq3/faLdcwFwOYBn6vN4EcB/rX9+LoAnARwA8EMApTbeoxsA3N+JedTHe67+99LSs9mhZ2QvgP31e/NTAENrMQ/13FMoMgj13FMoMghd+ApFBqELX6HIIHThKxQZhC58hSKD0IWvUGQQuvAVigxCF75CkUH8f1DAf7IiI0e5AAAAAElFTkSuQmCC" alt="" />

　　数据预处理。将输入图像像素除以255进行归一化，将标签数据扩充为$one\_hot$编码，并且查看数据规模。

X_train = X_train_orig / 255.
X_test = X_test_orig / 255.
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print("number of training examples = " + str(X_train.shape[0]))
print("number of test examples = " + str(X_test.shape[0]))
print("X_train shape: " + str(X_train.shape))
print("Y_train shape: " + str(Y_train.shape))
print("X_test shape: " + str(X_test.shape))
print("Y_test shape: " + str(Y_test.shape))
conv_layers = {}

Result:
number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)

1.1 - Create placeholders

# GRADED FUNCTION: create_placeholders

def create_placeholders(n_H0, n_W0, n_C0, n_y):
    """
    Creates the placeholders for the tensorflow session.

    Arguments:
    n_H0 -- scalar, height of an input image
    n_W0 -- scalar, width of an input image
    n_C0 -- scalar, number of channels of the input
    n_y -- scalar, number of classes

    Returns:
    X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
    Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
    """

    ### START CODE HERE ### (≈2 lines)
　　 # tf.placeholder第一个参数为类型，第二个参数位数据规模，可通过name参数指定变量名
    X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
    Y = tf.placeholder(tf.float32, [None, n_y])
    ### END CODE HERE ###

    return X, Y

X, Y = create_placeholders(64, 64, 3, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))

Result:
X = Tensor("Placeholder_2:0", shape=(?, 64, 64, 3), dtype=float32)
Y = Tensor("Placeholder_3:0", shape=(?, 6), dtype=float32)

1.2 - Initialize parameters

　　通过$tf.contrib.layers.xavier\_initializer(seed=0)$初始化权重/过滤器/卷积核$W_1$和$W_2$，不用关心$bias\_variables$的初始化，因为TensorFlow方法会帮助我们做这件事，所以我们只需要初始化卷积方法的卷积核。TensorFlow也会自动初始化全连接层的参数。

　　使用TensorFlow初始化参数有如下语法：

W = tf.get_variable("W", [1,2,3,4], initializer = ...)

# GRADED FUNCTION: initialize_parameters

def initialize_parameters():
    """
    Initializes weight parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [4, 4, 3, 8]
                        W2 : [2, 2, 8, 16]
    Returns:
    parameters -- a dictionary of tensors containing W1, W2
    """

    tf.set_random_seed(1)                              # so that your "random" numbers match ours

    ### START CODE HERE ### (approx. 2 lines of code)
    W1 = tf.get_variable("W1", [4, 4, 3, 8], initializer=tf.contrib.layers.xavier_initializer(seed=0))
    W2 = tf.get_variable("W2", [2, 2, 8, 16], initializer=tf.contrib.layers.xavier_initializer(seed=0))
    ### END CODE HERE ###

    parameters = {"W1": W1,
                  "W2": W2}

    return parameters

tf.reset_default_graph()
with tf.Session() as sess_test:
    parameters = initialize_parameters()
    init = tf.global_variables_initializer()
    sess_test.run(init)
    print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
    print("W2 = " + str(parameters["W2"].eval()[1,1,1]))

Result:
W1 = [ 0.00131723  0.14176141 -0.04434952  0.09197326  0.14984085 -0.03514394
 -0.06847463  0.05245192]
W2 = [-0.08566415  0.17750949  0.11974221  0.16773748 -0.0830943  -0.08058
 -0.00577033 -0.14643836  0.24162132 -0.05857408 -0.19055021  0.1345228
 -0.22779644 -0.1601823  -0.16117483 -0.10286498]

1.3 - Forward propagation

　　在TensorFlow中，可以通过如下一些函数（语法）实现前向传播。

tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = 'SAME')
tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = 'SAME')
tf.nn.relu(Z1)
tf.contrib.layers.flatten(P)
tf.contrib.layers.fully_connected(F, num_outputs)

　　注意到，使用$tf.contrib.layers.fully\_connected$将会自动初始化全连接层的参数（权重），并且在训练模型的时候训练参数。因此我们无需初始化其参数。

　　实现方法$forward_propagation$，使其构造模型：CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED。

# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "W2"
                  the shapes are given in initialize_parameters

    Returns:
    Z3 -- the output of the last LINEAR unit
    """

    # Retrieve the parameters from the dictionary "parameters"
    W1 = parameters['W1']
    W2 = parameters['W2']

    ### START CODE HERE ###
    # CONV2D: stride of 1, padding 'SAME'
    Z1 = tf.nn.conv2d(X, W1, strides=[1, 1, 1, 1], padding="SAME")
    # RELU
    A1 = tf.nn.relu(Z1)
    # MAXPOOL: window 8x8, sride 8, padding 'SAME'
    P1 = tf.nn.max_pool(A1, ksize=[1, 8, 8, 1], strides=[1, 8, 8, 1], padding="SAME")
    # CONV2D: filters W2, stride 1, padding 'SAME'
    Z2 = tf.nn.conv2d(P1, W2, strides=[1, 1, 1, 1], padding="SAME")
    # RELU
    A2 = tf.nn.relu(Z2)
    # MAXPOOL: window 4x4, stride 4, padding 'SAME'
    P2 = tf.nn.max_pool(A2, ksize=[1, 4, 4, 1], strides=[1, 4, 4, 1], padding="SAME")
    # FLATTEN
    P2 = tf.contrib.layers.flatten(P2)
    # FULLY-CONNECTED without non-linear activation function (not not call softmax).
    # 6 neurons in output layer. Hint: one of the arguments should be "activation_fn=None"
    Z3 = tf.contrib.layers.fully_connected(P2, 6, activation_fn=None)
    ### END CODE HERE ###

    return Z3

tf.reset_default_graph()

with tf.Session() as sess:
    np.random.seed(1)
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    init = tf.global_variables_initializer()
    sess.run(init)
    a = sess.run(Z3, {X: np.random.randn(2,64,64,3), Y: np.random.randn(2,6)})
    print("Z3 = " + str(a))

Result:
Z3 = [[ 1.44169843 -0.24909666  5.45049906 -0.26189619 -0.20669907  1.36546707]
 [ 1.40708458 -0.02573211  5.08928013 -0.48669922 -0.40940708  1.26248586]]

1.3 - Compute cost

# GRADED FUNCTION: compute_cost 

def compute_cost(Z3, Y):
    """
    Computes the cost

    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3

    Returns:
    cost - Tensor of the cost function
    """

    ### START CODE HERE ### (1 line of code)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=Z3, labels=Y))
    ### END CODE HERE ###

    return cost

tf.reset_default_graph()

with tf.Session() as sess:
    np.random.seed(1)
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    cost = compute_cost(Z3, Y)
    init = tf.global_variables_initializer()
    sess.run(init)
    a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})
    print("cost = " + str(a))

Result:
cost = 4.66487

1.4 - Model

　　整合上面实现了的有用的方法去构建一个模型在SIGNS数据集上进行训练。

　　将有几个步骤：

　　* 1 create placeholders

　　* 2 initialize parameters

　　* 3 forward propagate

　　* 4 compute the cost

　　* 5 create an optimizer

　　最后，创建一个$session$然后循环$num\_epochs$，每一次获得一个$mini-batches$并且通过模型预测出结果计算损失并且优化他们。

# GRADED FUNCTION: model

def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
          num_epochs = 100, minibatch_size = 64, print_cost = True):
    """
    Implements a three-layer ConvNet in Tensorflow:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

    Arguments:
    X_train -- training set, of shape (None, 64, 64, 3)
    Y_train -- test set, of shape (None, n_y = 6)
    X_test -- training set, of shape (None, 64, 64, 3)
    Y_test -- test set, of shape (None, n_y = 6)
    learning_rate -- learning rate of the optimization
    num_epochs -- number of epochs of the optimization loop
    minibatch_size -- size of a minibatch
    print_cost -- True to print the cost every 100 epochs

    Returns:
    train_accuracy -- real number, accuracy on the train set (X_train)
    test_accuracy -- real number, testing accuracy on the test set (X_test)
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    ops.reset_default_graph()                         # to be able to rerun the model without overwriting tf variables
    tf.set_random_seed(1)                             # to keep results consistent (tensorflow seed)
    seed = 3                                          # to keep results consistent (numpy seed)
    (m, n_H0, n_W0, n_C0) = X_train.shape
    n_y = Y_train.shape[1]
    costs = []                                        # To keep track of the cost

    # Create Placeholders of the correct shape
    ### START CODE HERE ### (1 line)
　　 # 1 create placeholders
    X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
    ### END CODE HERE ###

    # Initialize parameters
    ### START CODE HERE ### (1 line)
　　 # 2 initialize parameters
    parameters = initialize_parameters()
    ### END CODE HERE ###

    # Forward propagation: Build the forward propagation in the tensorflow graph
    ### START CODE HERE ### (1 line)
　　 # 3 forward propagate
    Z3 = forward_propagation(X, parameters)
    ### END CODE HERE ###

    # Cost function: Add cost function to tensorflow graph
    ### START CODE HERE ### (1 line)
　　 # 4 compute the cost
    cost = compute_cost(Z3, Y)
    ### END CODE HERE ###

    # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
    ### START CODE HERE ### (1 line)
　　 # 5 create an optimizer
    optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
    ### END CODE HERE ###

    # Initialize all the variables globally
　　 # 初始化全部变量
    init = tf.global_variables_initializer()

    # Start the session to compute the tensorflow graph
　　 # 创建一个会话，并开始执行
    with tf.Session() as sess:

        # Run the initialization
        sess.run(init)

        # Do the training loop
　　　　　# 训练num_epoches轮
        for epoch in range(num_epochs):

            minibatch_cost = 0. # 保存当前mini_batch的cost
            num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
            seed = seed + 1
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed) # 随机从训练集中获取一个mini_batch

            for minibatch in minibatches: # 遍历mini_batch中的训练数据，计算损失

                # Select a minibatch
                (minibatch_X, minibatch_Y) = minibatch
                # IMPORTANT: The line that runs the graph on a minibatch.
                # Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
                ### START CODE HERE ### (1 line)
                _ , temp_cost = sess.run([optimizer, cost], feed_dict={X:minibatch_X, Y:minibatch_Y})
                ### END CODE HERE ###

                minibatch_cost += temp_cost / num_minibatches

            # Print the cost every epoch
            if print_cost == True and epoch % 5 == 0: # 每5轮输出一次当前损失值
                print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
            if print_cost == True and epoch % 1 == 0: # 取偶数轮数的损失值来画折线图
                costs.append(minibatch_cost)

        # plot the cost
　　　　 # 画出损失值折线图
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        # Calculate the correct predictions
　　　　 # 计算预测准确率　　
        predict_op = tf.argmax(Z3, 1)
        correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))

        # Calculate accuracy on the test set
　　　　　# 计算训练集准确率以及测试集准确率并且打印出来
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
        print(accuracy)
        train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
        test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
        print("Train Accuracy:", train_accuracy)
        print("Test Accuracy:", test_accuracy)

        return train_accuracy, test_accuracy, parameters

_, _, parameters = model(X_train, Y_train, X_test, Y_test)

  Result:

Cost after epoch 0: 1.921332
Cost after epoch 5: 1.904156
Cost after epoch 10: 1.904309
Cost after epoch 15: 1.904477
Cost after epoch 20: 1.901876
Cost after epoch 25: 1.784078
Cost after epoch 30: 1.681051
Cost after epoch 35: 1.618206
Cost after epoch 40: 1.597971
Cost after epoch 45: 1.566706
Cost after epoch 50: 1.554487
Cost after epoch 55: 1.502187
Cost after epoch 60: 1.461036
Cost after epoch 65: 1.304490
Cost after epoch 70: 1.201760
Cost after epoch 75: 1.163242
Cost after epoch 80: 1.102885
Cost after epoch 85: 1.087105
Cost after epoch 90: 1.051911
Cost after epoch 95: 1.018554

 

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYUAAAEWCAYAAACJ0YulAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xl8HWXZ//HPlb1Z22brvu90YQnQQoFiUUBABMqiIgoosii4PY/gBrjwAwQB5UFAhIJoRRERUZCdAm2BllLovreUtlm6JmnTbNfvj5mGtCRtWnIySc73/XodkzNzn5lrmHq+mXtm7jF3R0REBCAh6gJERKT9UCiIiEgDhYKIiDRQKIiISAOFgoiINFAoiIhIA4WCdEpm9oyZfSXqOkQ6GoWCtCozW21mJ0Vdh7uf6u4PR10HgJm9YmZfa4P1pJrZg2a23cw2mtl399P+O2G7beHnUhvNG2BmL5vZDjNb3Hifhuu5w8zWm9kWM7vHzJJjuW3SdhQK0uGYWVLUNezWnmoBbgCGAv2BE4H/NbNTmmpoZicD1wKTgQHAIODGRk2mAXOBXOBHwONmlh/OuxYoAkYDw4DDgR+37qZIZNxdL71a7QWsBk5qZt7pwLvAVmAGMLbRvGuBFUA5sBA4q9G8rwJvAHcAm4FfhNNeB24DtgCrgFMbfeYV4GuNPr+vtgOB6eG6XwD+D3i0mW2YBKwDfgBsBP4IdAOeBkrD5T8N9Anb/xKoA6qACuDucPoI4Plwe5YA57XCf/sPgc80ev9z4C/NtP0zcFOj95OBjeHvw4BdQFaj+a8Bl4e/zwbObTTvi8AHUf/b06t1XjpSkDZhZocDDwLfIPjr8z7gqUZdFiuA44Acgr9YHzWzno0WcTSwEigg+KLdPW0JkAfcCvzBzKyZEvbV9s/AW2FdNwBf3s/m9AC6E/xFfhnBEfdD4ft+wE7gbgB3/xHBF+o33T3T3b9pZhkEgfDncHu+ANxjZoc0tbKwe2ZrM6/3wjbdgF7AvEYfnQc0ucxw+t5tC80sN5y30t3Lm1mWhS8ave9jZjnNrEs6EIWCtJWvA/e5+5vuXudBf/8uYDyAu//N3de7e727PwYsA45q9Pn17v5bd691953htDXu/nt3rwMeBnoChc2sv8m2ZtYPOBL4qbtXu/vrwFP72ZZ64Hp33+XuO919k7v/3d13hF+kvwRO2MfnTwdWu/tD4fa8A/wdmNJUY3e/0t27NvMaGzbLDH9ua/TRbUBWMzVkNtGWsP3e8/Ze1jPANWaWb2Y9gKvD6enNbrF0GO2pP1Q6t/7AV8zsW42mpRD8dYuZXQR8l6B/G4IvprxGbT9oYpkbd//i7jvCP/wzm2i3r7Z5wGZ337HXuvruY1tK3b1q9xszSyfo2jqFoCsJIMvMEsMQ2lt/4Ggz29poWhJBV9TBqgh/ZhN0Ve3+vbzp5lSE82nUlrD93vP2XtYvga4EXYG7gN8DhwElB1m7tCM6UpC28gHwy73+yk1392lm1p/gi+WbQK67dwXms2cXRayG890AdA+/2HfbVyA0Vcv3gOHA0e6eDRwfTrdm2n8AvLrXf4tMd7+iqZWZ2b1mVtHMawGAu28Jt2Vco4+OAxY0sw0Lmmhb7O6bwnmDzCxrr/m717XT3b/p7r3dfRCwCZjTTABKB6NQkFhINrO0Rq8kgi/9y83saAtkmNlp4RdPBsEXZymAmV1McGVLzLn7GoITpzeYWYqZTQDOOMDFZBGcR9hqZt2B6/eaX0xwdc9uTwPDzOzLZpYcvo40s5HN1Hh5GBpNvRqfM3gE+LGZdTOzEQRddlObqfkR4FIzGxWej/jx7rbuvpTgKOD6cP+dBYwl6OLCzHqbWa9wP44HftLENksHpVCQWPgPwZfk7tcN7j6b4EvqboIrdJYTXBWEuy8EbgdmEnyBjiG42qitfAmYQPAX7y+Axwi6RVrqTqALUAbMAp7da/5dwJTwmv7fhOcdPgNcAKwn6Nq6BUjlk7me4IT9GuBV4Ffu/iyAmfULjyz6AYTTbwVeDtuvYc8v9gsILjvdAtwMTHH30nDeYIKrxyoJzs9c6+7PfcLapZ0wdz1kR6QxM3sMWOzu+utX4o6OFCTuhV03g80sIbzZ60zgyajrEomCrj4SCe47eILgPoV1wBXuPjfakkSioe4jERFpoO4jERFp0OG6j/Ly8nzAgAFRlyEi0qHMmTOnzN3z99euw4XCgAEDmD17dtRliIh0KGa2piXt1H0kIiINFAoiItJAoSAiIg0UCiIi0kChICIiDRQKIiLSQKEgIiIN4iYUyip2ccNTC9hVq+eAiIg0J25C4c2Vm5k6YzXf/9t71NdrvCcRkaZ0uDuaD9ZpY3uydvMIbnl2MfmZqfzk9JGEz+kVEZFQ3IQCwOUnDKJ4exUPvrGK/KxULprQn7TkRBITFA4iIhBnoWBm/PT0UZRW7OKWZxdzy7OLAUhJSqBLciJpyQmkJSeS0OgIwgySEowEM8yM3UONu4Pv9Tx2w3CcunoP5++eHvyPQbgcPva53dPq6p06D5ZR7059fTA9KdFISUwgOTGB5KQEUhKNxARjZ3Ud23bWUF5VS1pyInmZKeRmplKYnUrPnC706tqFkT2zGNkjmwSFn4jsR1yFAkBCgvHr88YxaVg+myurqaqpZ0dNLbtq6tlZXUdVbR27HzHhEH4xO7WNzkMYQVg0/jJv/FiKxAQjIcEwPgqG+jAlnOCLvnEwuIfzw882vIKVYBi19fVU1wavmnqnprae2vp6uqan0C83g6y0JKqq6yirrKZ4exXvrdtKWUV1wzryMlOYOCSPI/p3Y3B+JoMLMinISlUXmojsIe5CASA1KZFzi/pGXUbMVdXUsX7rTt5Zu5XXlpXy2rIynnx3fcP8ySMKeOArRQoGEWkQl6EQL9KSExmUn8mg/EymHNEHd2fj9ipWllby3IKNPDxzDa8vL+O4ofsdYl1E4kTcXJIqwTmVnjldOHZIHj88bSQ9c9K464Vl6JGsIrKbQiFOpSYlcuWJQ5i9ZgtvLN8UdTki0k4oFOLYeUV96JmTxp0vLNXRgogACoW4lpqUyJWTButoQUQaKBTi3HlH9qVHdhp3v7ws6lJEpB1QKMS51KREzjy0F++s2UptXX3U5YhIxBQKwtDCLKrr6lmzeUfUpYhIxBQKwrDCTACWFZdHXImIRE2hIAwpCEJhaXFFxJWISNQUCkJ6ShJ9u3dhqY4UROKeQkEAGFaQxTIdKYjEPYWCAMHJ5pVlFdToCiSRuKZQECA42VxT56zZVBl1KSISIYWCADCsMAvQyWaReKdQEAAG52dihk42i8Q5hYIA0CUlkb7d0llWoiMFkXgWs1AwswfNrMTM5jczP8fM/mVm88xsgZldHKtapGWGFWbqBjaROBfLI4WpwCn7mH8VsNDdxwGTgNvNLCWG9ch+DC3MYlVZpa5AEoljMQsFd58ObN5XEyDLggcEZ4Zta2NVj+zf7iuQVpfpCiSReBXlOYW7gZHAeuB94Bp3b/JPVDO7zMxmm9ns0tLStqwxrgwt0BVIIvEuylA4GXgX6AUcCtxtZtlNNXT3+929yN2L8vP1kPlYGVKQSYKuQBKJa1GGwsXAEx5YDqwCRkRYT9xLS06kX/d0lpUoFETiVVKE614LTAZeM7NCYDiwMsJ6hOBk85srN/O1h99mRWkliQnGHecdypg+OVGXJiJtIJaXpE4DZgLDzWydmV1qZpeb2eVhk58Dx5jZ+8CLwA/cvSxW9UjLHDc0j8rqWtZt2cnInlnsrK7jvPtm8uz8jVGXJiJtwNw96hoOSFFRkc+ePTvqMjo1dye4KAxKy3dx2R9nM3ftVn742RFcdvzgiKsTkYNhZnPcvWh/7XRHs3zM7kAAyM9KZdrXx3PKIT246T+L+UCP7BTp1BQKsl9pyYl881NDAHhv3baIqxGRWFIoSIsMLcwkOdF4/0OFgkhnplCQFklNSmRYYRYL1isURDozhYK02OheOcz/cBsd7eIEEWk5hYK02Og+OWzZUcOHW3dGXYqIxIhCQVpsdK9gFJL5H26PuBIRiRWFgrTYyJ7ZJCaYziuIdGIKBWmxtOREhhZkMl9XIIl0WgoFOSCH9Mrh/Q+362SzSCelUJADMrp3NmUVuygp3xV1KSISAwoFOSCjewejpaoLSaRzUijIARnVMxszdGezSCelUJADkpGaxKC8DF2WKtJJKRTkgI3unaPLUkU6KYWCHLAxvXPYsK2Kjduqoi5FRFqZQkEO2KTh+SQnGjc8tUCXpop0MgoFOWBDCrL4/meG8+yCjTz29gdRlyMirUihIAfl68cN4tghudz4r4UsL6mIuhwRaSUKBTkoCQnGr887lLTkBK75y1yqaur2mF9WsYtr/jKXRRt0lZJIR6JQkINWmJ3GrVPGsWD9dq54dE5DMFTsquXih97mn++u5zcvLou4ShE5EAoF+UQ+PaqQm84aw8tLSvnGH+dQXlXDFY/OYeGG7Rw9sDvPLSymeLuuUhLpKBQK8ol98eh+3HLOGKYvK+X4W1/mtWVl/L+zx3DLOWOpq3edjBbpQBQK0irOP7Ift54zlvKqWv73lOGcV9SXAXkZHDc0j2lvraW2rj7qEkWkBRQK0mrOLerL/BtP5spJQxqmfenofmzYVsUrS0ojrExEWkqhIK0qLTlxj/eTRxZSkJXKn95cE1FFInIgFAoSU8mJCVxwZF9eWVrK6rLKfbbdUV3Lrtq6fbYRkdhKiroA6fwuOKofv3t1BZN//Srj+uQwcWg+wwuzKMhOJS8zlffWbeVf8zYwfWkp4wfn8sglR0VdskjcUihIzPXq2oUnrzqWZ97fyGvLy7j7pWXU7zVkUo/sNI4e1J3pS0t5Y3kZxw7Ji6ZYkThnHW1As6KiIp89e3bUZcgnsL2qhg+37KSkfBel5bvon5vOEf26UV1Xz4m3vUJhdhr/uPIYzCzqUkU6DTOb4+5F+2unIwVpc9lpyWT3TGZkzz2npyUkcvXkoVz3xPu8uKiEk0YVRlOgSBzTiWZpV6Yc0YcBuenc9twS6vfuYxKRmFMoSLuSnJjAdz49jMUby3li7odRlyMSdxQK0u6cMbYXI3tm8/2/zePkO6Zz+3NLeHPlJkq2V+mhPiIxFrMTzWb2IHA6UOLuo5tpMwm4E0gGytz9hP0tVyea48PmymqenPsh/12wkbdXb264Wik9JZEj+nfjprPG0Ld7erRFinQgLT3RHMtQOB6oAB5pKhTMrCswAzjF3deaWYG7l+xvuQqF+LOpYhfvf7iNtZt3sLK0kr/PWQcGN589ltPG9tz/AkQk+quP3H26mQ3YR5MvAk+4+9qw/X4DQeJTbmYqk4YXNLy/dOJAvjVtLlf9+R2eeKeA7hkpONAlOZFD+3blqIHd6dOtC/UeHHG4OwXZadFtgEgHEuUlqcOAZDN7BcgC7nL3R5pqaGaXAZcB9OvXr80KlPapb/d0/nb5BO54fin/mPsh7mAG5VW1/HFWMMZSZmoSldW17D4QvvnsMVxw1Ef/djZXVnPH80v56rEDGJyfGcVmiLRLMb15LTxSeLqZ7qO7gSJgMtAFmAmc5u5L97VMdR9Jc+rrnaUl5by9egvLi8vJSU8hLzOF/y7YyKyVm3n44qOYODSPLZXVfPGBN1m0YTvj+uTwxJXHkpigG+Wkc4u8+6gF1hGcXK4EKs1sOjAO2GcoiDQnIcEY0SObET2y95h+1mG9mfK7mVzxpzk89NUjuf6pBaworeCrxwxg6ozVPDxjNZdMHBhR1SLtS5SXpP4TOM7MkswsHTgaWBRhPdJJZaUl8+DFR5KWnMiUe2eyrLiC+758BNefMYoTh+dz23NL+GDzjqjLFGkXYhYKZjaNoEtouJmtM7NLzexyM7scwN0XAc8C7wFvAQ+4+/xY1SPxrXfXLvzhK0WM6pnN7y48nBOHF2Bm/OKsMQD86Mn5ugdCBA2IJ8JDb6zixn8t5KIJ/fnep4eTk54cdUkira4jnFMQaRcumjCAFaUV/HHWGp6at55rJg/lC0f1+9hT5ETigY4UREIL12/npv8s4vXlZaQmJXDUwO5MHJLH2D5d6Z+bTo/sNBJ0lZJ0UJHf0RwrCgWJJXdn1srNvLComNeWlbK0uKJhXkpSAoPzMxnVM5tRvbKZNDxf9zhIh6FQEGkFJdurWFpcwepNlazZVMnS4goWbthOafkukhKMS48byDWTh5KekkTlrlqeX1hMQoJxxtieekiQtCs6pyDSCgqy0yjITmPi0D0fD7ph207ueH4p9726kqfnbeDw/t14YWExO2vqAHhxUTG3nDNW5yWkw9GRgsgn8Naqzfzkyfls3F7FZ8f05POH9mL2mi3c9twSRvfK4bZzx1Gxq5Y1myoBOGNcL5ITNWK9tD11H4m0IXffo7vohYXFfPuxd6nYVbtHuxE9srjp7DEc3q9bW5cocU6hIBKxVWWVvL6slN7dutA/N4PlJRVc/88FFJdXcdH4/vzwtJGkJql7SdqGzimIRGxgXgYD8zIa3g/Oz+SYwbnc9t8lPDxzDYs3lnP/l4t0s5y0K+rcFGlDWWnJ3HjmaO664FDmrt3KOffO0LhL0q4oFEQicOahvXnk0qMo2V7FWffM4MOtO6MuSQRQKIhEZvygXB6/4hh2Vtfyg8ff22NAvtq6ev7z/gaqwktcRdqKQkEkQsMKs/jhaSN5fXkZj765FoC6eue7f53HlX96hzue3/PxIlU1dVwy9W1eWlwcRbkSBxQKIhH74lH9OG5oHv/vP4tYXVbJD/7+Hk/NW8+A3HQemrGa9Y26lu55ZQUvLS7h1meXaKhviQmFgkjEzIxbzhlLohmfu/t1Hp+zju+cNIxHv3Y0ONz5QnC0sGZTJfe+uoJeOWks3ljO68vLIq5cOiOFgkg70KtrF356xii2V9Vy5aTBXD15CH26pfPlCf15fM46lhWXc+O/FpKcYDz2jQnkZ6Xy+9dWRV22dEItCgUzO7cl00Tk4J1b1JdZ103mf04e3nB39FUnDiEjJYnL/jiHlxaX8O2ThtG3ezpfmdCf6UtLWbKxPOKqpbNp6ZHCdS2cJiKfQI+ctD2Gy+iekcJlxw9iVVklQwsy+eqxAwD40tH9SUtO4A+vr4yoUums9nlHs5mdCnwW6G1mv2k0KxuobfpTItKaLj1uIGs27+CiCf0bBtPrlpHClCP68Ne31/E/J48gPys14iqls9jfkcJ6YDZQBcxp9HoKODm2pYkIQHpKEredO46xfbruMf2SYwdSU1/Pfa+uiKgy6Yz2eaTg7vOAeWb2Z3evATCzbkBfd9/SFgWKSNMG5WdyflFfHnxjFZ8d21Mjr0qraOk5hefNLNvMugPzgIfM7NcxrEtEWuBHp42kR3Ya3//bPN39LK2ipaGQ4+7bgbOBh9z9COCk2JUlIi2RlZbMrVPGsbK0ktv+uyTqcqQTaGkoJJlZT+A84OkY1iMiB2ji0DwuHN+PP7yxirdWbY66HOngWhoKPwP+C6xw97fNbBCwLHZliciBuO7UkRRmpemks3xiLXrIjrv/Dfhbo/crgXNiVZSIHJiM1CROHFHA0/PWU1fvJCbY/j8k0oSW3tHcx8z+YWYlZlZsZn83sz6xLk5EWm78oO6U76pl4frtUZciHVhLu48eIrg3oRfQG/hXOE1E2onxg3IBmLlSA+XJwWtpKOS7+0PuXhu+pgL5MaxLRA5QYXYag/IymLVSJ5vl4LU0FMrM7EIzSwxfFwKbYlmYiBy48YNzeXvVZmrr6qMuRTqolobCJQSXo24ENgBTgItjVZSIHJzxg3Ip31XLAp1XkIPU0lD4OfAVd8939wKCkLghZlWJyEEZP7A7ALNW6kBeDk5LQ2Fs47GO3H0zcFhsShKRg1WQncbg/AyFghy0loZCQjgQHgDhGEgtusdBRNrW+EG5vL16i84ryEFpaSjcDswws5+b2c+AGcCt+/qAmT0Y3tcwfz/tjjSzOjOb0sJaRGQfxg/KpWJXLfN1XkEOQotCwd0fIbiDuRgoBc529z/u52NTgVP21cDMEoFbCIbQEJFWcPQgnVeQg9fSIwXcfaG73+3uv3X3hS1oPx3Y3wXT3wL+DpS0tA4R2beCrDSGFmTy3IKNUZciHVCLQ6G1mVlv4Czg3ha0vczMZpvZ7NLS0tgXJ9LBXTi+P++s3cqbOlqQAxRZKAB3Aj9w9/0+GcTd73f3Incvys/XjdQi+3P+kX3Jy0zl7peXR12KdDBRhkIR8BczW01wM9w9Zvb5COsR6TTSkhP5+nEDeW1ZGXPX6sm50nKRhYK7D3T3Ae4+AHgcuNLdn4yqHpHO5kvj+9M1PZn/09GCHICYhYKZTQNmAsPNbJ2ZXWpml5vZ5bFap4h8JDM1iUuOHcgLi0pYsH5b1OVIB2HuHnUNB6SoqMhnz54ddRkiHcK2nTVMvPklhhRmctu54xicnxl1SRIRM5vj7kX7axflOQURibGcLsn87POHsKy4gpPvmM4NTy1gS2V11GVJO6ZQEOnkzjqsDy9/fxLnHdmXR2au5tS7XmNFaUXUZUk7pVAQiQP5WancdNYYnvrmRGrr6zn/vlksLS6PuixphxQKInFkdO8c/nLZeBIMLrh/lp7nLB+jUBCJM0MKsnjsGxNITUrgkqlvU1ffsS42kdhSKIjEoYF5GVx76gg2bq9i3rqtUZcj7YhCQSROnTAsn8QE46VFGo9SPqJQEIlTXdNTOKJ/N15arFCQjygUROLYp0YUsHDDdjZs2xl1KdJOKBRE4tjkEQUAOlqQBgoFkTg2pCCTvt278LJCQUIKBZE4ZmZ8angBry8vo6pmv482kTigUBCJc58aWUhVTT0zV+gpbaJQEIl7Rw/sTnpKos4rCKBQEIl7acmJHDskjxcXFevuZlEoiAicc3gf1m+r4pGZq6MuRSKmUBARTj6kkOOH5XP7c0vZuK0q6nIkQgoFEcHM+MWZo6mpq+fGfy2IuhyJkEJBRADol5vO1ZOH8sz8jby0uDjqciQiCgURafD14wYxpCCTnzy5QN1IcUqhICINUpIS+NWUsWzbWcNZ97zB4o16CE+8USiIyB4O69eNx74xnnp3pvxuJq8tK426JGlDCgUR+ZhDeuXwjyuPpU+3Llwy9W1Wl1VGXZK0EYWCiDSpV9cuTL34KOrqncfnrIu6HGkjCgURaVaPnDSOG5rPE++so153O8cFhYKI7NM5RwR3O89cqQHz4oFCQUT26TOjCslKS+Lv6kKKCwoFEdmntORETh/bi2fmb6RiV23U5UiMKRREZL+mHNGHnTV1/Of9DVGXIjGmUBCR/Tq8X1cG5mXoKqQ4oFAQkf0yM6Yc0Ye3Vm1m/ofboi5HYkihICItcv6RfemRncbXH5lN8XaNi9RZKRREpEXyMlP5w1eL2L6zhkumvk2lTjp3SgoFEWmxQ3rlcPeXDmfxxnK+NW0utXX1UZckrSxmoWBmD5pZiZnNb2b+l8zsvfA1w8zGxaoWEWk9Jw4v4MbPHcJLi0u4/NE57KjWEUNnEssjhanAKfuYvwo4wd3HAj8H7o9hLSLSii4c35+fnxkEwwX3z6KkPDjHUFaxi5cXl6hrqQNLitWC3X26mQ3Yx/wZjd7OAvrEqhYRaX1fnjCAnjld+Na0uXzut2+QnprIytJgNNWzD+vNr88/NOIK5WC0l3MKlwLPRF2EiByYk0YV8tg3xlOYk8bA3AyuPXUEXziqH0/M/ZA3NVZShxSzI4WWMrMTCUJh4j7aXAZcBtCvX782qkxEWmJsn67886pjG97vrK5j+tJSfvLP+fz76uNITmwvf3tKS0S6t8xsLPAAcKa7N/tnhbvf7+5F7l6Un5/fdgWKyAHrkpLIDZ87hKXFFUx9Y3XU5cgBiiwUzKwf8ATwZXdfGlUdItL6Pj2qkMkjCrjzhaUs2rAddz2LoaOwWO0sM5sGTALygGLgeiAZwN3vNbMHgHOANeFHat29aH/LLSoq8tmzZ8ekZhFpPWs37eDkO6ezs6aObunJjOvblatOHMKRA7pHXVpcMrM5LfmOjVkoxIpCQaTjWLtpB68tL2XeB1t5ZUkp9Q4vfvcEctKToy4t7rQ0FHQGSERipl9uOl86uj+3ThnHg189ks2Vu7j52cVRlyX7oFAQkTYxuncOl04cyLS31vL26s0N01eXVbJh284IK5PGFAoi0ma+8+lh9O7aheueeJ/FG7dz9bS5nHj7K1xw/yyqazWOUnugUBCRNpOeksQvPj+a5SUVnHLnazy/sJgzxvZizaYd/OXttVGXJ7SDm9dEJL6cOKKAb580lJ3VdXz9+EHkZqRQUl7Fb15cxtmH9yEzVV9LUdKRgoi0uW+fNIzrPjuSvMxUzIwfnDKCsopqHnhtZdSlxT2FgohE7rB+3Th1dA9+P30lZRW7Pja/clctK0orIqgs/igURKRd+P7Jw6mqrefmZxZTV//R/VMbt1Vx1j1v8Jk7pvPv9zZEWGF8UOediLQLg/MzuXTiQO6fvpK1m3dw+7njqK13LnzgTbbtrGFUz2yu/stcEgxOHdMz6nI7LYWCiLQb1506gmGFWdzw1AJOves1UpKCzoxpXx/PwPwMvvLgW3xr2lzuNjhltIIhFtR9JCLthpkx5Yg+PHPNcYzunU1GaiJ/u3wCY/rkkJmaxNSLj2Rsnxy+NW0uS4vL9/jslspqHp6xml21dRFV3zkoFESk3enbPZ2/XDaBV79/IoPzMxumZ6Ul8/uLishMTeK6J96nPjz3UF/vfOev73L9Uwt4dJbud/gkFAoi0m4lJNjHpuVmpvKj00YxZ80W/vxWEAAPzVjNK0tK6Z6Rwr2vrqCqRkcLB0uhICIdzjmH9+aYwbnc8sxiXlpczM3PLOKkkYXc86XDKS3fxZ/e1NHCwVIoiEiHY2bcdNYYquvquWTqbHIzUvnVlLGMH5TLhEG5Olr4BBQKItIhDcjL4LufHkZSgvHr88fRLSMFgG+fNHSPo4XNldW8sLBYIdFCesiOiHRo26tqyE7b86E9X/z9LJZsLGdwfiaz12ym3uG8oj7cOmVcRFVGTw/ZEZG4sHcgAHzvM8PYtrOG8l21fPNTQ7loQn/+Onsd/5gGiSaUAAANK0lEQVS7rk1rq9xVyytLStp0nZ+Ubl4TkU7niP7dWfCzk0lNSgSgtq6exRvL+dE/5jOmd1cG5WXw1Lz1/O6VFVw4oT9fHt8/JnX89qXl3PvqCl763gkManRpbXumUBCRTml3IAAkJSbwmwsO49S7pnPFo3NITU5g/ofbyUpN4oanFjA4P4NjBuc1tF9WXE73jBRyM1MPev01dfU8Pic4MpmxYlOHCQV1H4lIXOiRk8avzz+UZSUVbKms4Y7zx/HGdZ9iQG463/rzXNZv3UldvXPXC8s4+c7pXPHoO59ofS8vLqGsYhcJBjNXbmqlrYg9HSmISNw4cXgBL37vBHp37UJacnAkcd+Xi/j8/73B5Y/OITM1iRkrNjGsMJO3Vm/mrVWbOWpg94Na119nf0BBVipHD8pl5ooy3B2zj9+M197oSEFE4srg/MyGQAAYUpDJ7eeN471123hn7RZuPWcs/7xqIrkZKdzzyvKDWkfx9ipeXlLKOUf04bgheZRVVLOspGM8D0JHCiIS904+pAdTLz6SPt3SGVIQ9P1fMnEgv/rvEhas38YhvXIOaHmPz1lHXb1zXlFfksKhOmau2MSwwqxWr7216UhBRASYNLygIRAALhzfn6zUJO55ZcUBLcfd+dvsDzhqYHcG5mXQt3s6vbt2YeaKjnFeQaEgItKEnC7JXDihP/95fwMr93oU6LadNcxYUcaM5WV7DNVdV+/8Y+6HrN60g/OL+jZMnzA4l1mrNjWM6tqeqftIRKQZlxw7kAdfX8V5980kLzOVtORENldWs3bzjoY2GSmJHD8sn24ZKTy3YCNlFdX07tqFzzZ6Otwxg3N5fM46Fm8sZ1Sv7Cg2pcUUCiIizcjPSuWms8bwytJSqmrqqKqpo3fXLpx/ZF9G986htq6eFxeX8NKiErburGbyiEJOG9uTE4cX0CXlo5PZEwbnAjBjRZlCQUSkIzvniD6cc0SfZudPHlmIf96pq3eSEpvuke+Z04UBuenMWrmJrx03KFaltgqdUxAR+YTMrNlA2G3C4FzeXLWZunZ+XkGhICLSBk4Ylk95VS23PruY9jw6tUJBRKQNnHxIDy4c34/7pq/kjueXRl1Os3ROQUSkDZgZP/vcaGpqnd+8tJzaemd4jyyWFVeweUc1V5wwmL7d06MuU6EgItJWEhKMm84eQ01dfcNNcYkJRqIZ76zZwhNXHkN6SrRfyzFbu5k9CJwOlLj76CbmG3AX8FlgB/BVd/9kwxKKiLRziQnGr84dx3lH9qVbegoD8zKYuXITFz/0Fv/z+Hvc/YXDIh04L5bnFKYCp+xj/qnA0PB1GfC7GNYiItJuJCYY4wflMrxHFilJCZwwLJ//OXkE/35vA/dNXwkEw2VU1dRRXVvfpiemY3ak4O7TzWzAPpqcCTziwdbOMrOuZtbT3TfEqiYRkfbq8hMGMf/Dbdz67GIefH0VW3fWUF1bDwQhkp6cyKXHDeTbJw2LaR1Rdl71Bj5o9H5dOE2hICJxx8y4dcpYCrPT2FFdS056Mjldkqmvd3bW1LGzuv6AR2s9GFGGQlOdZk0eI5nZZQRdTPTr1y+WNYmIRCYjNYmfnjEq0hqivE9hHdC30fs+wPqmGrr7/e5e5O5F+fn5bVKciEg8ijIUngIussB4YJvOJ4iIRCuWl6ROAyYBeWa2DrgeSAZw93uB/xBcjrqc4JLUi2NVi4iItEwsrz76wn7mO3BVrNYvIiIHTmMfiYhIA4WCiIg0UCiIiEgDhYKIiDSw9vywh6aYWSmw5iA/ngeUtWI5HUU8bnc8bjPE53bH4zbDgW93f3ff741eHS4UPgkzm+3uRVHX0dbicbvjcZshPrc7HrcZYrfd6j4SEZEGCgUREWkQb6Fwf9QFRCQetzsetxnic7vjcZshRtsdV+cURERk3+LtSEFERPZBoSAiIg3iJhTM7BQzW2Jmy83s2qjriQUz62tmL5vZIjNbYGbXhNO7m9nzZrYs/Nkt6lpjwcwSzWyumT0dvh9oZm+G2/2YmaVEXWNrCh9h+7iZLQ73+YR42Ndm9p3w3/d8M5tmZmmdcV+b2YNmVmJm8xtNa3L/ho8g+E34/faemR1+sOuNi1Aws0Tg/4BTgVHAF8ws2scbxUYt8D13HwmMB64Kt/Na4EV3Hwq8GL7vjK4BFjV6fwtwR7jdW4BLI6kqdu4CnnX3EcA4gm3v1PvazHoDVwNF7j4aSAQuoHPu66nAKXtNa27/ngoMDV+XAb872JXGRSgARwHL3X2lu1cDfwHOjLimVufuG9z9nfD3coIvid4E2/pw2Oxh4PPRVBg7ZtYHOA14IHxvwKeAx8MmnWq7zSwbOB74A4C7V7v7VuJgXxMM+d/FzJKAdILnune6fe3u04HNe01ubv+eCTzigVlAVzPreTDrjZdQ6A180Oj9unBap2VmA4DDgDeBwt1PtQt/FkRXWczcCfwvUB++zwW2untt+L6z7fNBQCnwUNhl9oCZZdDJ97W7fwjcBqwlCINtwBw6975urLn922rfcfESCtbEtE57La6ZZQJ/B77t7tujrifWzOx0oMTd5zSe3ETTzrTPk4DDgd+5+2FAJZ2sq6gpYR/6mcBAoBeQQdB1srfOtK9botX+vcdLKKwD+jZ63wdYH1EtMWVmyQSB8Cd3fyKcXLz7UDL8WRJVfTFyLPA5M1tN0DX4KYIjh65hFwN0vn2+Dljn7m+G7x8nCInOvq9PAla5e6m71wBPAMfQufd1Y83t31b7jouXUHgbGBpeoZBCcGLqqYhranVhP/ofgEXu/utGs54CvhL+/hXgn21dWyy5+3Xu3sfdBxDs25fc/UvAy8CUsFmn2m533wh8YGbDw0mTgYV08n1N0G003szSw3/vu7e70+7rvTS3f58CLgqvQhoPbNvdzXSg4uaOZjP7LMFfj4nAg+7+y4hLanVmNhF4DXifj/rWf0hwXuGvQD+C/1Od6+57n8DqFMxsEvB9dz/dzAYRHDl0B+YCF7r7rijra01mdijBifUUYCVwMcEfep16X5vZjcD5BFfbzQW+RtB/3qn2tZlNAyYRDJFdDFwPPEkT+zcMyLsJrlbaAVzs7rMPar3xEgoiIrJ/8dJ9JCIiLaBQEBGRBgoFERFpoFAQEZEGCgUREWmgUJB2w8xmhD8HmNkXW3nZP2xqXbFiZp83s5/GaNk/3H+rA17mGDOb2trLlY5Hl6RKu9P4XoMD+Eyiu9ftY36Fu2e2Rn0trGcG8Dl3L/uEy/nYdsVqW8zsBeASd1/b2suWjkNHCtJumFlF+OvNwHFm9m44dn6imf3KzN4Ox4r/Rth+kgXPj/gzwQ17mNmTZjYnHG//snDazQSjar5rZn9qvK7wDtBfhWPzv29m5zda9iv20fMK/hTeIISZ3WxmC8NabmtiO4YBu3YHgplNNbN7zew1M1sajtW0+/kPLdquRstualsuNLO3wmn3hUPFY2YVZvZLM5tnZrPMrDCcfm64vfPMbHqjxf+L4I5wiWfurpde7eIFVIQ/JwFPN5p+GfDj8PdUYDbBgGiTCAaCG9iobffwZxdgPpDbeNlNrOsc4HmCO90LCe4S7RkuexvBGDIJwExgIsEds0v46Ci7axPbcTFwe6P3U4Fnw+UMJRinJu1Atqup2sPfRxJ8mSeH7+8BLgp/d+CM8PdbG63rfaD33vUTjCH1r6j/HegV7Wv3AFIi7dlngLFmtntsmxyCL9dq4C13X9Wo7dVmdlb4e9+w3aZ9LHsiMM2DLppiM3sVOBLYHi57HYCZvQsMAGYBVcADZvZv4OkmltmTYFjrxv7q7vXAMjNbCYw4wO1qzmTgCODt8ECmCx8NklbdqL45wKfD398ApprZXwkGlNuthGDkUYljCgXpCAz4lrv/d4+JwbmHyr3enwRMcPcdZvYKwV/k+1t2cxqPnVMHJLl7rZkdRfBlfAHwTYJRWRvbSfAF39jeJ++cFm7XfhjwsLtf18S8Gnffvd46wv+/u/vlZnY0wUOJ3jWzQ919E8F/q50tXK90UjqnIO1ROZDV6P1/gSssGBYcMxtmwQNl9pYDbAkDYQTBI0l3q9n9+b1MB84P+/fzCZ5m9lZzhVnwrIocd/8P8G3g0CaaLQKG7DXtXDNLMLPBBA/IWXIA27W3xtvyIjDFzArCZXQ3s/77+rCZDXb3N939p0AZHw25PIygy03imI4UpD16D6g1s3kE/fF3EXTdvBOe7C2l6cctPgtcbmbvEXzpzmo0737gPTN7x4NhtXf7BzABmEfw1/v/uvvGMFSakgX808zSCP5K/04TbaYDt5uZNfpLfQnwKsF5i8vdvcrMHmjhdu1tj20xsx8Dz5lZAlADXAWs2cfnf2VmQ8P6Xwy3HeBE4N8tWL90YrokVSQGzOwugpO2L4TX/z/t7o/v52ORMbNUgtCa6B891lLikLqPRGLjJoKHyncU/YBrFQiiIwUREWmgIwUREWmgUBARkQYKBRERaaBQEBGRBgoFERFp8P8BRxbXOg1qMQsAAAAASUVORK5CYII=" alt="" />

 

Tensor("Mean_1:0", shape=(), dtype=float32)
Train Accuracy: 0.666667
Test Accuracy: 0.583333

fname = "images/thumbs_up.jpg"
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64))
plt.imshow(my_image)

Result:
<matplotlib.image.AxesImage at 0x211fe84c748>

 

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAP4AAAD8CAYAAABXXhlaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJztfWmsZMd13nd6ffvMm33lKpIitZCSaIkyHYeiLFtSBOtHJMNLDMYgwD9KICMOLCkBAjtIAOmP7fwIDBCRY/5wLMmWbQqKYFuhRSsKJJJDkZJIDkczHA5nhrO/Zd7Sr/fKj+5365xz+9a73e+97qHv+YDB1O2qW1V3qXfPqXPOd8g5B4PBkC3kRj0Bg8EwfNjCNxgyCFv4BkMGYQvfYMggbOEbDBmELXyDIYOwhW8wZBCbWvhE9FEiOkFEp4jo81s1KYPBsL2gQR14iCgP4KcAPgLgPIDnAPyac+6VrZuewWDYDhQ2ce77AZxyzp0GACL6CoBPAkhc+Lt2zbqjhw9t2PGN40tIgbobZ5bJCM1/EOhrHqD/wClbPdsw9GguUDcItuL96GcenfHOnX8T8/MLG564mYV/GMA5dnwewAdCJxw9fAjf+puvdo+S56ZvmUt5E4OtUj9XSihrtFPMaDOPP91DD/VPrI9Yb/yH2Hrm5znWzKlmvJ0eIWH+lHxd8RoKVfYN0UVsHo6124LBYpI0O9Zju94vJ8XmGHponffxlz7xL1NNbzM6fq+7E3sPiegxIjpGRMfm5hc2MZzBYNgqbOaLfx7AUXZ8BMAF3cg59ziAxwHg3ne9I+UHMNAs/Inruy4uvKYbwLnAX98t+Tqxsfq46KShYz3wD1CgdXBs9qVyKa+ZAtpCvCqhMtRJALIL/cyoZ7uewyX1SaGvelDEYiU+D/VsA13oththM1/85wDcQUS3ElEJwK8C+MYm+jMYDEPCwF9851yTiP4NgL8DkAfwJ865l7dsZgaDYduwGVEfzrlvAfjWFs3FYDAMCZta+P3Cgas6WklJ1rES+wuoNSEtMLjB7xIP5HgBxS+tb0R819ajLawGg20acP08tGMe0+P5Ybvlf16Wm7OuXo3KuR17RF2uPMaGCo1FvZp12ybcg2T1PLXBMXTN8f3+kH7Oq9K1i20vJJ6ljkKvVZ/mI3PZNRgyCFv4BkMGMVRRv4N1mYTUry7WoicGNJUl9dnXWAmOFrqXlIJhXORLstcE5deAcBjQabgYHbulbV+38vqrUbn2+nHRLO98u8Lh20Td9N3v9Qc5/32JOcdwMT1otUxnVgypT+qk1DVpe2wHnbr6t0P340jUr6OYffENhgzCFr7BkEHYwjcYMoih6/heHUtrcJO6X0iHS+vaGja3hZTO3nPUuljIJBOEaNqHrTKxWWCfILCnUp2/GpWvvvxiVC47qcMWi8WoXLtySdSN3+ZNfYXxicA0UurnATOrfGRpdWm9L5PuvQrPMegHnap/ubcT+i4n75GlgX3xDYYMwha+wZBBjMCctw4lqoSkUoZ2WsagsEteSqSN+grEXveBQc5KG48f9jiTIvz86yej8tryclTOT0yKdrlcPiq3W7KPZq3mzxsb55NSc2TTCHjkhcDF+7i5MIlfYTCSlfjrl6AyBd7TcJw97zm9Otyvldu++AZDBmEL32DIIIYv6ifu6qc4ZaBxemFr2d1C7G3h1mnZK5IHCI+dzjutVa+JuusX34zKjXrTl8tSnM+3fABPs70m6iqL81G5vGNn4nyTZ6UdD9OxrMQIKRJ22vt5ZqlVppRvaihIJy3d2GbfYPviGwwZhC18gyGDsIVvMGQQw/fcWy/EosXSetYNiq3V6znS6/QDziPAk5H+tOSzGlWpn9eWl/xZDa/jt5st0a7F9H8qyG/I9fNnovKOIzdH5VxBvnJBqlBu4t0KfZeZLR3pkUOee8lHyTPpZw+LR0qy+6guOuw0aJ57BoNhA9jCNxgyiBEE6fQm4gh7SyWJUMp7SaZKCfQ/IIddwhRTJkbpa+RBeQdDfBVJaK5JUb++xrzu2lzeluY8x8x5+byowupVbxKsLF6LylO798s++LcnpTOdzn2QltNf8Nf3oT6F36t0kO9OOpNgPNnP1qmr9sU3GDIIW/gGQwZhC99gyCBGF53ntJGkf179YJfB/GqByKkgv3/vKLC47p9M5iG5NkJzTOaiT08omdS3nFez0RBVjXqdjeV/b7WkOc8VvGJPkEp+vuX7uHj8R1H5tg98SLYrlnvOCZDvBIXyGCQeBDTyfogyRPRfOirO0LsTHCuUTDDkq90nNvziE9GfENEVInqJ/baLiL5NRCe7/89ubhoGg2GYSCPq/ymAj6rfPg/gKefcHQCe6h4bDIa3CDYU9Z1z3yWiW9TPnwTwULf8BICnAXxuw9EcImklbplItoGl9krigU0xc43r1Sw+VuAIqdWRkFgackdLKcq5pGtJG48HcYO0Nx33amsw8b6movgKjC8/RhrBJrZ09rWofGn3AdHs0N3v7n2SOgze7xDHSELvsXdKBMWFvPg2T+ARyi0Q7m/05rz9zrmLAND9f9+WzchgMGw7tn1Xn4geI6JjRHRsfmFh4xMMBsO2Y9Bd/ctEdNA5d5GIDgK4ktTQOfc4gMcB4N3vfIfzIuGglNTJKkFIRIvvxvbff3qkFQcHu87QUFzFSUsukS+VZWXefw/qLIBntaKb+Z38ovqGtJi6UGAzefOVF0W72aO3ROXxqZngjNfRj5oln3suoRWULB4MHQqOlzyPgPqQMHTacKBOY9r4JIZBv/jfAPBIt/wIgCcH7MdgMIwAacx5fw7g+wDuIqLzRPQogC8C+AgRnQTwke6xwWB4iyDNrv6vJVR9eIvnYjAYhoQReO5t1iSRTEaYXjsfjC8/SU/rz9NwQMbHpGYD8kLww8LYmKjjx6uLi1G5WpXmvFrNp8kql5TnXsmn18qXWaqtylXR7trZ16Py0XvulZNM4KzXzyH9/k1yHyJNu9PprrkHYXKfYbNzb6/PXsdp+thspJ756hsMGYQtfIMhgxiqqN9x3OuIK2nNGxt2mPDDVnAWxCXxJCaOwA+ps7f26sePnLJh4mmhHgpjE6JuYo/3x7p4xovitVpTtMszuXdivCjqds56Lv0iY+kYz8u5X33tlah84Pa7RF2xnJR6K2T8TRecFW+VLIqL89IGAaWaRY9fgtmDkwO3kvvuDfviGwwZhC18gyGDsIVvMGQQIyPiiKm+AR0uiaAidViWhgjdS8unnqxLUiDKLpjqOHVe6FD/ad1Lk2tyOfka7H3b3VH55IsvROVGRZrzWsy1d1xF+DWZSYynNh8bk+7BleueiPPamZOi7sBd7+o5336Md/JtSdbx0/eX1rk85JIuIYg+0lLzbzcRh8Fg+KcHW/gGQwYxZFHfJZvEgva3QUwX6Uxg/fCryxN9f20lsgeltYCaQQlhWv2IpWm9F0N97r75tqh86B2eKOPksz+QDZmoX2tIPr6xFhf1fblUlma/PEu9dflVGbk3c/BIVB6fCaXaThu9mExgklqFDI0lzKfJ71+MPzDxndBqRXLoXr+Sv33xDYYMwha+wZBBjGxXP7VXHOSuZyhYIy1nXVB0lsRsiXXBeQTzWKUMEEra6cVGvG+8XcpRVWW+6MXxt3/w56Ly/Lkzot3SFc+/0myrTLp8V7/tyzk12OT0tJ/vyrKou3rKe/UdvfcBNkH5vaLAlablWkza/e/UBTzmUuth/e//hyw28efZn53CvvgGQwZhC99gyCBs4RsMGcTwdfyuKtJX9BxTcuNecv0jpIILbTEQdcf1StdXburAXkbCWIN6mQ0MduEzu32k3k33SE+6ny4+HZVbLTnLJtPrGw0f1Vdn6bkAYGp6Mirvnt0h6havnInKlYXbo/LkHplqW0Lr4EnEJ8keeDFrW4gAcxAOjZilLykyMMTUkt4zsBfsi28wZBC28A2GDGL4ov4AknparvjUnQcDgnhNMrdb2nn0Y7aUusUWqDSButSmPpYm68g73i2qzv3EB/BUGDcfADTrPgNvteiJOCprVdFuquZF/+mZSVnX8HVzr/4wKpff989Fu+K4JBIRGOA29pPeTTYLtUunXwrzI2l1ZAvYZbqwL77BkEHYwjcYMghb+AZDBjEyc15/6kr/Bq3gGQHPXgowIaTWi8U5gT5i9sJBRgiNvfl2fBbTu/eKuv13eHLM08e+L+qazIRXZXr8akXq+Csrq1G5VJDc/OPMdbi5dDkqXzv+nGi3910fiMqFoswRgAR372B+vLQvT/zMtJ2kxPYZctOk0DpKRN8houNE9DIRfbb7+y4i+jYRnez+P7ttszQYDFuKNKJ+E8DvOOfuBvAAgM8Q0T0APg/gKefcHQCe6h4bDIa3ANLkzrsI4GK3vExExwEcBvBJAA91mz0B4GkAn9uwP9+xrBDeeQnnJPfWPQq4WCVIZLG+U8q9QQ61IOEDaxfi3KdQH1tn1ukHlJei+FFm3jv7kx+KumrF59Qm9nmpKm6+BjP7tWrSqw85L+pPMa6+6+dPiWZzbF577nm/6qLk58ErXPK7058Clo4kZqAnljI6NDCNRPS1uUdEtwB4D4BnAOzv/lFY/+OwL/lMg8FwIyH1wieiKQBfB/DbzrmlPs57jIiOEdGx+YXFjU8wGAzbjlQLn4iK6Cz6P3PO/VX358tEdLBbfxDAlV7nOuced87d75y7fxdLq2QwGEaHDXV86ticvgzguHPuD1jVNwA8AuCL3f+f3NRMkswuullQf06KcgIc88N0Af056FIrkKwTDq6B91biYvpiyrwA240d+w9F5Z37Doi6qyz9dU7tDXC02/5aNGlps+VZfUosdfdYURJ2Vt44EZXnCiVRt+eu90ZlyrPXPfbgk98/EZ0XUN7Tprse2CDYm4t1IKSx4z8I4DcB/ISI1mlQ/wM6C/5rRPQogLMAPr25qRgMhmEhza7+95D8R+nDWzsdg8EwDIyAbDPJdS+dx5wUyTTJZeJZagrJrnvpiRCSESZuDCHh2gJkmzqlU/JMBkOo93zZm9j23nyrqJvjoj5/ZoygAwAanLBD5yeoe++/Vot5/JFUHfLwJsHrp34i6krTu6LyjqOezCNG6BKg1Q+TsyQgZi4MNBX9D/rMnPo/DPPVNxgyCFv4BkMGMXRRf12Ujgsk6XjHB+GUB8I7+UnnhfgYCIw3vtWUzVpe9CTFNy/aKXGwxXaxKefFWSrLwBMh6pP62809IHk5p//GpyX94BedLANP7pwRVUWWGiufI1aW8ygU/A69UyJ8jd/HpvfqyyvvP8fuQbsug4CunXo5Kk8dvIn1IS0DQS7HoIWF1YUsA0kd6qHS7tzHHoXx6hsMhg1gC99gyCBs4RsMGcQNlDsvUOsSDxJ7TZ3jLKDIax28vrQQlVfO+QixNiOJAICxvNf/i0qnLTH9lHIqUm1tLSpXWDk/JfnmV2q+/9WKjGhrMk84x/TYwpTUwXcf8fou584HgCLzkhNed/oesr2NyqU3RVWBXTfPncf3LgCgzqLzViproi7H9lH43kBZeQLm+H6I2vNYnfee5LUVH2IyvnM30iK4q5TwXg3qERpM3diHzr8R7ItvMGQQtvANhgzihvTcC/FT9Oqp54kh60zAS6vd9KLn/OkTom7uuCeboLXrUXl8TImek+P+QAWUNNnEiiVppisykTVX82appWtXRbuZvV40X1R1q2u1qNxgYv/5SzJ4cnqHVx8mZqQqMbnTR1HO7PFjTeyQ7Gr5Nhf1z4u6iQl/D2pNL7LrdNrLKytReWV1VdSVy0VW9l6CbSXOT7L7nVNmuhbj9FtduBaVx3dIUT8U/OW4WVTXIQmp2WQCHqda5eXenIozsE+HP/viGwwZhC18gyGDsIVvMGQQo0uTHYrAi5FopFT6A7p7kp2kWa+JZud/9ExUXjgpI72IuZDm+ZxaUm91zNw2wXRTACgW/S1vrjVEHfK9TWBrS1L33bffX8zOsiSeADOPtYu+P24qBIDSjqmoTKuSEm1xwe8bXDv1alQeK0n9eeeUz1mnqTYmmN5dZLeH7zsAELn54GTkXovd40bDX1etLkcrsnuQU+ZT7ra8Ouf3OfbcfCdUQ1aWVSE/Wv5uDhwLmeASHNfbuak50EkK2BffYMggbOEbDBnEDWTO27qegfTmjcunJUf7qz/4ru+jJb3i2k0/Qp6J5ZMlKW5PM/G+XpdqQJGdl1NzLBS4BxqLaMvLv8+cf37HhDQJcmKOKhP7y2qwEjucUuoCV352zHgii5wSJ8cZ1/1aTapMLZZCyzERXgf4Efv2TEzLNNlj3IQnIiCVmsjJPfLyOgssSnCNqTCtpny2+aJUyZKQWu3cEvTD/W+ivsFg2AC28A2GDGIEon7/In5KNj7lAJWOU+3SmdOi2YVzfue3rfjhCkUvihfL/tatlORtXGWi89SYFKPLTJzXonOee/WxAJ6yUiWWFnywSUGRUnB+u3bDi7OT41KU5QEw1JZEIvt3eU8+LrIXimospj64mCcZE0vZTn5OPRe+P99uyvuNsm9bKvn555U4X2T3P6Y+Mc/J2qr3tqxXVkS78Z3s/gxTmlcI5PBFiF87SCTSA/bFNxgyCFv4BkMGYQvfYMgghq7jp1KflAdX0jn9EXby6D/uESb1Wz5yoyX7a+e5t55vmWtKk12r7SPrKsrMVWJKaLEgPdAKTG8rsgi0gopGG1v2+mlZewYynT/Hym87dFi0a7sWayevs1bxnoJVZjqcnJ6W7dh11xvSPMatXjl273PKNMmPdY6ACiPmKLF9kzG1b1Lk6dH0vgm7p601n7p7ZV5GK/ZDzMGx1UbpENmryPmwyX2IDb/4RDRGRM8S0Y+I6GUi+v3u77cS0TNEdJKIvkpEpY36MhgMNwbSiPo1AA875+4FcB+AjxLRAwC+BOAPnXN3AFgA8Oj2TdNgMGwl0uTOcwDWZcti958D8DCAX+/+/gSA3wPwxxuOuC4DBl3rks0Y6T2UlOFPWEJ8//tukamf3A/+X1Ru1KTJp9nwom2zzQJqnLyNnFNeCsDAChOPCyqgZJyZnsaZ6Uy3W13zqgRhWQ7AxF5ixrKJMekVNzXOAluK8l5dX2JBO0xdaC/LYCFuO2vHDK1+zs4xb0Ul6ssgF/3MvDpVYyqTgzL7MXfAojJvgvPxsf6uX3hDNONBO5oXkBIPUnO/DIYQif+GjcNItblHRPluptwrAL4N4DUAi865dQX5PIDDSecbDIYbC6kWvnOu5Zy7D8ARAO8HcHevZr3OJaLHiOgYER2bn1/o1cRgMAwZfZnznHOLAJ4G8ACAnUS0LlcdAXAh4ZzHnXP3O+fu37VrtlcTg8EwZGyo4xPRXgAN59wiEY0D+AV0Nva+A+BTAL4C4BEAT/Y1coBIQOfHE3p9MLldoH8SSn5UvOmue0Sz+x7+xaj8/b/936JuaXE+KnP33WpN6epjXlcvKTdXMPfVtbok4lhe9eYrHsVX0uQSLvkmNGp+D6HNzJHT03K3Yd/snqi8Y0rqtO2GP2/hOiMVnZLzLRT9PgFpMx1zOc4XQ/kOGBGnIjRpJ5hgtblX5OZT7rzcrbjA+PhX52QuhPqa388Zm5Tko6nTOmwBwmnak9HvtNLY8Q8CeIKI8uhICF9zzn2TiF4B8BUi+i8AXgDw5T7HNhgMI0KaXf0fA3hPj99Po6PvGwyGtxhGlyY7YBaBNteIDkK846Fxe7crKB72t91xe1S+9uohUXf+DW9GW1715bVVyWe3zDjyymV5i3kKLZ0yuslMfQ2mBjgdJcg9/FQaLh6lRcysCKVW4JpXW5auy/tYq/novysL3rS376BMtTU+5udbVGQeBc70wcx5pIkscpxHTl5nWzwnZpbTO1P8PKUu8PPKbI4rVWmq5aL/2KRMNxYSudMK4yECD+FVyn9XrCVptdw0MF99gyGDsIVvMGQQww/S6coo/QTYSKQUcmLNejNxLJx7TbS6+MOno/JteydE3e373hmV60wsv67ory9f8+LxpavSd2Hxuhcx6w0lfrNb0GZybrMpA4l40Esxr0R93o6JufW6vL/LTCUoKJFycc1fT42lFBvfKYN0OMkFVKASsYzBOS6zt9SOPNtp14+MB9hw2uy8kvXbrM+muqd8xz9Hydd8/eLZqLzr6O2irrOv3XuOgyDMBxlQCUQKLVXX5xzsi28wZBC28A2GDMIWvsGQQYwghVZHhwk73SVH56V11qOAEtSoelPcyWe/J5o1Gfd6SenPPP1VseT1voP7dol2Rw/ujcotZV5aXvI6/uVrUv8/f8GncZ5f9O0qNel1V616nb+pTH1C3616fXe5VRXtxpmpT3vTzVV826kJbwLTY3GVUxOTigxjTP93MRJUHrmXnF6Lk4iSUpLzgmFT1rXY/WizFN3KkoqVa97jvF6REY9jU96TL5SZLWajFg0DlLGBawt0qI6MV99gMGwAW/gGQwYxAl79LrRIE4qEYKIQ52+PcZKlFJMqSz7w5NLZc6KuuerFPB1gU2JcbyUm6k9OSt67iTIn1FAZZqd9FtndO6W58M5bDkblWt2L9/WqNOc1Gkx8VbeqwvjyanV/XmU1OR1YTfECvjHnVZA5xu9HSj7maoz2QhTedIy0hHvqdZr5PoSnIaTkzAN4SJHnE7sfMZGXNc0F+A4rFe+tuHRFBpqWRdDOYAa9EF++9tBLRkDl7TNKx774BkMGYQvfYMggbOEbDBnE6HT8AdMNJxtFwoF7vDGPgqvWpIvnWsXrwrmc1ItLLMKNm/PW6oo7nxFPjKl9gjGmW5byUs8ssRxwnDRiZmpctCswF1KnlPxlxpG/vOp55NvKJFhnf/NnpveLOrCIwrWz/tr0Hgo/zuk6Vm6zZx1rx/V1/U7wPIBMx2+odnxvQOvLebFvwPaH1DxyLM/A/Fnpxr3n5jt8u5zcs0lCnHCk1yx6n8kmmdin3hawNNkGg2FD2MI3GDKI0Yn6MYSEeFYT4JuTXSSbTKZnvafd9IEjot3c3I/ZWCqSjEV+jTGTXastxb8yUwNqKlpshZuX1GVywb/EVIKi4nkvkn9s+i/3KhPveSTg0qpUR6ZmD/g5qsi9xhoznbHftbWUm8f0RFpcvOciu/Lwa7Uosc4xrz5uxs0rUxxC6gJL7ZVnVtFCSfXBzlu+cl5UVVmegYmde5CEtNx8Qe8/MSWl0rB7oEX7fhVn++IbDBmELXyDIYMYQZBOioqQJ1PAcy+twFMe87vk7/nwL4m6K1c9F93VN8+KuhLjAswzsbShyCXARMqmzvZEfKdaBdiwFF3c8y2v+sixsfWtWqt60bZW8xOpKaIMMEtEbUVyBi5c915sVeb911YWhAYj6Yh5TebY/BPY0Tsn8rIKsOGqVoBUhN//dkuRdDArB6fedk6qZ9zSwzkHAWDxkhf9J1VWXcGNERTvB0h/pQhHgt5/tqtvMBg2gi18gyGDsIVvMGQQwyfbXNdFQpF0IXWFR+rFopySO3HCa8v/fvCmm0W7j/3Gb0blH/zD/xF1J5//QVReXWFecQ1pGuJc7gUVccbVtrYy1ziW8qrZYLp1Q6WWYt6GmuiDmyCJDcb1fQC4/qaPQFurSFPf/Ko3A+aZ2UunuOZbD622Itvk82KnOe25x/YrCspMx/cNGswsql+PdpPp7morwxX94Dx9udP7MvzBqE7mmCff/ttlvthCyUds8nnFX+HkXBGSS5/vYSUb/mLLJ0QC0gOpv/jdVNkvENE3u8e3EtEzRHSSiL5KRKWN+jAYDDcG+hH1PwvgODv+EoA/dM7dAWABwKNbOTGDwbB9SCXqE9ERAP8CwH8F8O+oI488DODXu02eAPB7AP544JkIET71SYlHMc49kXGX22Bku/2Hfdqs+98rM+nOrDGCBiba1lV6qqXrnsxjtSJNZVXWtqlMbJxsgvPUaVGfi6nau6vNRH3uWae57vLM3DY9IYlElmuec09km1UehJzrPi578iy4zItPtQIX02PptZhXnzZH8pGYHa3ZlH2ssUfTZKpEXgVIJZF+AED97OmofOm146Lu0J0+10KO359+JO+EAJ7+hPftMef9EYDfhX+auwEsOufWFcfzAA73NbLBYBgZNlz4RPQJAFecc8/zn3s07fknh4geI6JjRHRsfn6hVxODwTBkpBH1HwTwy0T0cQBjAGbQkQB2ElGh+9U/AuBCr5Odc48DeBwA3vXOewYLwjcYDFuKDRe+c+4LAL4AAET0EIB/75z7DSL6CwCfAvAVAI8AeLKvkbUpKzyHqCxVyT60ILEBkDzayjWfLnnuxAui7tAeT7pY4Omulb6YzyXrrTz9dbUque4rjM9+edmTZq4sV0S7Fsulp1Vr7pZaZsQeOhKQc/OvyWlgetKTgJ6f83kGnDJz5XLekKNJP5stblbk5jZpVuSntWLc/HxfhhNqKoIKdr+bqv92y99vbo6MmSbZBeSUCbbIruXUc0+LusKYv1e7Dt7kfy9JI1eAVl9fDRIRiM4L+gv3wGYceD6HzkbfKXR0/i9voi+DwTBE9OXA45x7GsDT3fJpAO/f+ikZDIbtxnA99xy8JDNgqmAu/cW9l0LEZgkDKlH80usno/Ll83LbgknRyOV9dFdeiY3lIuPcnxgTdfx41+wOUbefp+IKuIFxLvpWQ4q2tar3wru+6AkkOEEHIEXbRlu+BhNFX8dJQHQKatf2ZkCnIsl4uq0cU4ViIiYT4VvKbMnTg7eFZ6AmYOGqlVIX+Hmcr0OJxtzLkatLADDG+iwszom60888FZUr7/DfwT1HbhHtJqdmWP+KBCQ10qWSSwPz1TcYMghb+AZDBjG6IJ1k9uH0fQU5ySR4wAP3YtPqwioLULm2ILOmclG0yDj3SIn6BdbpWEnRa/P0WuViYl2RWQ108EoOfJdciccs9dZ1lplXexDWmYfbmgrgWWXb/NyLrajSgXHrRV0HCzHRmRxPoSWaCZ497THHvRDb7Jrj3HzJbw9vy9WFWBou5smoLSCo+h9KSg2oXHszKp/5wd9F5blDt4t2B+68NyrvOSR5Hstlr/5ptTE1orWQbiXZF99gyCBs4RsMGYQtfIMhg7iBePVDSNJbkiPwYt5d4qxkbv4dB44TGAXIAAAUNElEQVRG5UZORa1VfKxBjpFhFIqK956lzVprSv25yFJSF5SeWWT6I087nVemslzADYyb91aW/R6F1osbda/vzi3J9ForjJiDm+UmxlU68AmW2mtNknlUeXQh34tR8+CEo/opc9IOTvShvfNkVKPy3ONen+x+55Suzm9pQaX8JrbXUKmoXAvMm7Hs/NjLb7wk2i1fu+TLd79X1O05fEtU3rVnX1QulTTFRfL77d/jdIY+++IbDBmELXyDIYO4IUX9uGCfkCIpRNsXCoQI8P0dvv3OqHznBx8Sdc9/x3tpra567vWSnggzDSkpXaSW0laonCALYeZHHQHD+1OiLSfwaHC1Qom2jTrzmIM0o60wIg7OUzc2pkV9b4aK8eBVvSpUZ+I85+IHNBlJcko0HpTS0oFPTL2pK+9C3gd/7LmWHKvAzGikEhk0mPm3qsYusG5KjN9Pm/3qSz74683n/1HUVeavROWVm/37d1B5/01MTvo55rQqa+Y8g8GwAWzhGwwZhC18gyGDGF3uvIB+Hgq6C50YSKAdqFMmtaI3ofzMQw+Luv1HPdHCyz88FpXPvPqyaLd43Zv9ykX5t5UHZsVcQ5nZyHFXU02oycgrWw1piuNEnMJNWQ/V4qYyWbfGdOYJ7k6q+iixiyFG3tEZz+8TFJh7cE3p+NztuqVzCSa48zbVvgbX67UbN3eBLZUZeYrafHHKzMjBCUd15F6p7O8BdwluKdJPHuXo2jJSssJMf/Ul/+40q9LNet+RW6PyztlZUddvxJ998Q2GDMIWvsGQQQxZ1GdMHC5Z4I4bJHqLrDmnTRq8w+T0Q0n9dVoxsa4gb89tb397VD56qxe7vvN1KW6/+dpPo/LamhTXri96M2CjrkxxTJzlhBIxvnlu3lNVxSLj3GMeheWCjKzbObvHz6Mm579c5WZAxlMX8CAcV1GIPIJwmXEJFvLSJMh5AVsteTHNNucF9H3klTmWk5tMTEriEy6aN+o8hbhSkVgEYV6ZykrMpDleUvyKIvW2n39dEaTwQMxSSd9HlhJt0afkvvyTFdFubcV7YlZvktF/s3s6z1N7aCbBvvgGQwZhC99gyCBG6LmXTK+tJVuXsCcf402Trl6J44nMubpZSm/AyvL1qJyvScKO2w557rymEl8ra7ujclWl3qox0Z9nh61WpVjKPfI00cfMjBd1x5mI2lZqRaXqRcLVhgywabGd9/HpaV/mQTkAiowgRJN0jLEAE04ksshowwGAxbVASdgiRVeOeQ3mCjooih9LUbfFAnq4Z+TEmAyA4SK72rgXGY+dygrcTAgyyqkXiVssWiodGBV6E300azIBzdwrz0bltevzou760dsAAHVF2Z4E++IbDBmELXyDIYOwhW8wZBAj1PEHI9EI+eDJVFuDMY+n7aNW8d5XS9cWRZ2rez2WlEkwX/K68PSkNG3t3umjrzhJh/ZoazCdn3RaK2KRcMxktazMS6uMbGOlLvXCMiMSmZ7yHnkz01Oi3cQY1+uVx1wuIcWY4r1fWvH3sVbXXn3+2ko8XXcs0tBfS115BvKNmRLbDxlTOj7fKykqwssa22+p1xXxCfMi5E/CqXen2WZkocqUWGqx+8NeiUJeEbUyj7/VM6+IurWFTqqz+prcQ0lCqoVPRGcALKNzbU3n3P1EtAvAVwHcAuAMgF9xzlk6XIPhLYB+RP0POefuc87d3z3+PICnnHN3AHiqe2wwGN4C2Iyo/0kAD3XLT6CTU+9zoRN4Bq0N8uOKo0GE9lg20QQTXn99+9ZTs94sV5rdJ1pdPeM995otZV5hYqrmy+e8+lzUz6lraTOxnRQXPYGTXvjyckWa7NaYea+oOANnD3qvvp0zXv0oKrVlihFD1JVJsJBnojSb/kRRmdGY9rBWVbx9LACJ8+prcpNS0cvHY055EDKTIJe+iyoj7vSkN1Vqz8AiC7SqqBemxi6unZAhGJBmP22v5m2JqTuuoNsxdcSp53mt4/HnmlKNSELaL74D8PdE9DwRPdb9bb9z7iIAdP/fl3i2wWC4oZD2i/+gc+4CEe0D8G0iejXtAN0/FI8BwKGDBwaYosFg2Gqk+uI75y50/78C4K/RSY99mYgOAkD3/ysJ5z7unLvfOXf/7OzOrZm1wWDYFDb84hPRJICcc265W/5FAP8ZwDcAPALgi93/n0wz4Lq5LGQqC9IFuuTzghF+ojKw08DnFdPFfHliyruyvu8jHxftvvctr2edPflTUccj8AoFpUsyPVxw/+tccczlU+v//L7WWK4/bkYEgFzZ69o7VUTb7IxXvKeY2aupTGWCsx4SPLcA15nbihOfm/eKU2rPo+HnzM8iRTrh2L5GWxGHcnMbd4POK+78OneDLst9CJHHMK/Mhew6W3lOpKL2ZUQOP9lFg6cUZ2Y/p117BXGoSs2e74yn3Z6TkEbU3w/gr7svVAHA/3LO/S0RPQfga0T0KICzAD6dbkiDwTBqbLjwnXOnAdzb4/c5AB/ejkkZDIbtxeg497Q/XrrAutTmt3iKoQ2ms36ecAxMp44cuPlmUfexf/VbUfnEj38k6t58/fWo3NKmF+apxlNhzV+5KpotzF3zpyjVp8E48UuM523PjPS6q7EorpLmy2emrQlW11QyKicZIXUnc+RF5/ExRpQxJtUKTirSaEsxmnPdMcsk2uqxNFgfsRwErO2OnV49q1Yk7x03JbZUBF651NvMCgAlllaMc+5xU2qnT8YfqER4PmeuPmmiGendKvsf65pk0zqsmq++wZBB2MI3GDIIW/gGQwYxAh0/gVjfJR6EqiQo3UYBhdpRz2LnODEwULacmt4Rld/34M+Luvf97D9jQ8fY7qMS1/Xmr1wTrZ79vz732ukTJ0Td8rxnZsnB68xrNak/15mpr9qQ+mKFufNyJh3N73991ev4ZeV+3GQ6Lo8yK+SlWbFcZm6uastjrcn0bqYXq7R3qHK2orokNx1n5sgSYwnKT0o2IX7vtY5fZ260BRW5N85Mf3xaNZXDj7vsVknW8dx//Em0VSRjnu3ZtNR+S6HPb7h98Q2GDMIWvsGQQYyMiEMTaoZk+NScGkIUD8jwQZPd4LF7vRDzUOSRWIEL41aj/YcPi7qPf/pXovLCNakGvH7Ch1Gce+1kVF6akybBJUbWuKa86a4uej73NjM1TSqPttUKI8ooKtIILvozs9R4WZoO+aNoK/NVve77X1r15reW+lzVW150bigTaYHNa2HRE6SOl+V8J5norznx64yPv6nMhTxdNb+2kiJBrax586nmvudRfSKHgk6FzU19SXXpsmTbF99gyCJs4RsMGcRwRX3OxBETxTc4bx2bl74H7sOJHf9kbn4KWAaCYyeI/vrXAkuHtffAQVG394APfX7fg96CUKtJQpCVJS/2XnzjtKg7c+J4VK4szkXl5Ybso77qjzVPXZkF0lTXvCg+OS539fklN5SIvcKsBvMrnksup9JYtViqrWJZ1lUYPyHnIJwYk6/+7I5kwhHHjvVuusibwK6lpIKi2iw4qx3LCuz74FmBtSooUpjprGopU2dFffXV2mAw/JOALXyDIYOwhW8wZBAjMOcleO4xJMckSW+3WAResmtdgKlf60b8b2Gyd6FUv9KTisjTUm429JEjgBM0FIq8LHXOSUYksv/wEVH37vf/bFSurXkz2pVzb4h2z//jU1F57sKbom6FRf+tVLxuXZKZnwUrRUN5u1WZzl9lhBq5urwfPLfdtOLLr1SZqY95JOqchq2Wz3+4i+n7gDRVFrXuzlNjMw+/MdWO7xuUiio6j5VrTRaR2JDthFepeiVa3X2CuDdob9gX32DIIGzhGwwZxNBFfS8Z9WHOS+orxJ0fiAEKaATQioXsnnrW6JTIvWfUY46xukRdInEeW2Pd1KKzF1OL0zNRefLud4l2B266NSq/cVISL7/6wvNR+cIp70G4uCwJMNoJnHgAUG1yLj1/b4qKq3BqwnvM0ar03HMs0IUHuTSUSW2lwjnx5RynWf/T0xOijov6DRZIpFNtc37/klK7xPNkn+Kaev0aTPQvKt5BTYSyEeyLbzBkELbwDYYMwha+wZBBDFnHdxG5QFoyzDhC/rCMdDElYUdoFnoPIRfUzzceK36eNkfyYu/9hH7GDvaR0kRIgX2TiSmv/9/9np8Rdbff886o/MYpn1vg9VePi3aXz5+LypcunBd19QWffrzZZEQZyt2bGMlIW11pkSnbeUYIoklKueGsUpP6PzHijGJJ7kMUWRQin2ODFFEGV8nVy5lnkXZ5puTncpqIw9e1Avn30sC++AZDBmEL32DIIIYq6jsECAMCXkmJybFCebIGtnNxcT5A0hEIwZPmPSXcU9KB7j+x+9SXSezvej+3I1lqDKUvl0flMU9scec7fT6Wt90jTYK1qo/Au3b5oqg7c9KbAc+/cTYqXzorowmvz/m0jXVFlMGJOBybYy6nzGFs+spfDmuMk7C4KiMUpya9qY+n3laOgSIdllORdHmeOp2Z6YoqTTan4NP8h7rPjZDqi09EO4noL4noVSI6TkQfJKJdRPRtIjrZ/X+2r5ENBsPIkFbU/28A/tY593Z00mkdB/B5AE855+4A8FT32GAwvAWQJlvuDICfB/CvAcA5VwdQJ6JPAnio2+wJAE8D+NxG/a2L+nrHnALiMXe1I5cs54Yo9/rc9Owxp2Q2vviOakBvEVUh77yUVbHu+7/Q0Dlyjsl04HEjSu/ztIg9PuFTex299W2i7uitt0dlnvV2QfEHPv+970bll575npoHI8Bg0jDpT14u+Zlx9WGlKnf1edOpCRkgxCE8+do6oy97v9nOfUFl9G3l2f1uyT7afT73NF/82wBcBfA/iegFIvof3XTZ+51zFwGg+/++vkY2GAwjQ5qFXwDwXgB/7Jx7D4BV9CHWE9FjRHSMiI4tMLuswWAYHdIs/PMAzjvnnuke/yU6fwguE9FBAOj+f6XXyc65x51z9zvn7p+d3bkVczYYDJvEhjq+c+4SEZ0joruccycAfBjAK91/jwD4Yvf/JzcczXlSwH48jYS2mDYyLaWOHCTK1PpzAid+6FrS9hGbTVqTXdD0yX/VacnZPAJm0fBjCuj/SZ6TsX0Zbp5NNn3mGZHF3n2SYPRDH/9lf6D051ee+35UrjOTWlF98nLMPMaJPfSUm4rPvlL1ew98vhOKEAQFblqV/XOiTBLRhGoebGxqyzrfNN26SmvH/7cA/oyISgBOA/gtdKSFrxHRowDOAvh0yr4MBsOIkWrhO+deBHB/j6oPb+10DAbDMDD0IB3vuaftbUx0ie08cPGem5ACXnGpEfZ9k/1zEZiLbulNdhTQJZJMhHFpPtm70CXmK5DtcgFdIkxUktC7S55HWt4TFxhLJjiW11gaG4vKP/sLHxN1leWlqHzm1ZejckOpBEU2gKoSnnUt5ZJX44QeIvuVEtPJk2/E0l/xYCrWv9OBOHxOOf3uUHccpIL56hsMGYQtfIMhg7CFbzBkEMOPzls3XcTsXEyfCVDdh9xVw8rkQD67yT8EouykGh/YJwjuIYTmlWwSHIzgJOA+HbzhyX3Itr31YGADl+B20n5FMqZndojjn/ulT0TlpUWfGnz+0gU5FNfx9T1lurbOe8dJQYhdZ7UmNwq4aU6bC/Ms7yB32dVjcbVe7xP0u8FlX3yDIYOwhW8wZBCkTQbbOhjRVQBvANgD4NrQBu6NG2EOgM1Dw+Yh0e88bnbO7d2o0VAXfjQo0THnXC+HoEzNweZh8xjVPEzUNxgyCFv4BkMGMaqF//iIxuW4EeYA2Dw0bB4S2zKPkej4BoNhtDBR32DIIIa68Inoo0R0gohOEdHQWHmJ6E+I6AoRvcR+Gzo9OBEdJaLvdCnKXyaiz45iLkQ0RkTPEtGPuvP4/e7vtxLRM915fLXLv7DtIKJ8l8/xm6OaBxGdIaKfENGLRHSs+9so3pGhUNkPbeETUR7AfwfwMQD3APg1IrpnSMP/KYCPqt9GQQ/eBPA7zrm7ATwA4DPdezDsudQAPOycuxfAfQA+SkQPAPgSgD/szmMBwKPbPI91fBYdyvZ1jGoeH3LO3cfMZ6N4R4ZDZe+cG8o/AB8E8Hfs+AsAvjDE8W8B8BI7PgHgYLd8EMCJYc2FzeFJAB8Z5VwATAD4IYAPoOMoUuj1vLZx/CPdl/lhAN9Ex8l/FPM4A2CP+m2ozwXADIDX0d172855DFPUPwzgHDs+3/1tVBgpPTgR3QLgPQCeGcVcuuL1i+iQpH4bwGsAFp1z6yRyw3o+fwTgd+EjeXaPaB4OwN8T0fNE9Fj3t2E/l6FR2Q9z4fcKH8qkSYGIpgB8HcBvO+eWNmq/HXDOtZxz96HzxX0/gLt7NdvOORDRJwBccc49z38e9jy6eNA59150VNHPENHPD2FMjU1R2feDYS788wCOsuMjAC4ktB0GUtGDbzWow8H0dQB/5pz7q1HOBQCcc4voZEF6AMBOIloP1R7G83kQwC8T0RkAX0FH3P+jEcwDzrkL3f+vAPhrdP4YDvu5bIrKvh8Mc+E/B+CO7o5tCcCvAvjGEMfX+AY6tOBAWnrwTYI6wedfBnDcOfcHo5oLEe0lop3d8jiAX0BnE+k7AD41rHk4577gnDvinLsFnffhH5xzvzHseRDRJBFNr5cB/CKAlzDk5+KcuwTgHBHd1f1pncp+6+ex3ZsmapPi4wB+io4++R+HOO6fA7gIoIHOX9VH0dElnwJwsvv/riHM4+fQEVt/DODF7r+PD3suAN4N4IXuPF4C8J+6v98G4FkApwD8BYDyEJ/RQwC+OYp5dMf7Ufffy+vv5ojekfsAHOs+m78BMLsd8zDPPYMhgzDPPYMhg7CFbzBkELbwDYYMwha+wZBB2MI3GDIIW/gGQwZhC99gyCBs4RsMGcT/B1hbLUZmsTyqAAAAAElFTkSuQmCC" alt="" />

1.5 - References

https://web.stanford.edu/class/cs230/