关于fftshift----将零频率的分量移到频谱的中心

fftshift

作用：将零频点移到频谱的中间

用法：

Y=fftshift(X)

Y=fftshift(X，dim)

描述：fftshift移动零频点到频谱中间，重新排列fft,fft2和fftn的输出结果。将零频点放到频谱的中间对于观察傅立叶变换是有用的。

fftshift就是对换数据的左右两边比如 x=[1 2 3 4] fftshift(x) ->[3 4 1 2] IFFTSHIFT Inverse FFT shift.（就是fftshift的逆）（IFFTSHIFT undoes the effects of FFTSHIFT.

x=[1     2     3     4     5];

y=fftshift(x)

y =

4     5     1     2     3

ifftshift(y)

ans =

1     2     3     4     5

需要fftshift的原因：

1、在matlab中，经过fft变换后，数据的频率范围是从[0,fs]排列的。

2、而一般，我们在画图或者讨论的时候，是从[-fs/2,fs/2]的范围进行分析。

3、因此，需要将经过fft变换后的图像的[fs/2,fs]部分移动到[-fs/2,0]这个范围内。而fftshift就是完成这个功能。通常，如果想得到所见的中间是0频的图像，经过fft变换后，都要再经过fftshift。

=================================================================================================================================

一.对于实信号：

因为实信号以fs为采样速率的信号在 fs/2处混叠，所以实信号fft的结果中前半部分对应[0, fs/2],后半部分对应[ -fs/2, 0]；

1）实信号fft的结果前半部分对应[0, fs/2]是正频率的结果,后半部分对应[ -fs/2, 0]是负频率的结果。大于fs/2的部分的频谱实际上是实信号的负频率加fs的结果。故要得到正确的结果，只需将视在频率减去fs即可得到频谱对应的真实负频率；

2）如果要让实信号fft的结果与[-fs/2, fs/2]对应，则要fft后fftshift一下即可，fftshift的操作是将fft结果以fs/2为中心左右互换；

3）如果实信号fft的绘图频率f从[-fs/2, fs/2]，并且没有fftshift，则fft正频谱对应f在[0, fs/2]的结果将混叠到(f - fs/2)的位置;

fft负频谱对应f在[-fs/2, 0]的结果混叠到 f + fs - fs/2 的位置，注意这里f为负值，也就是说此种情况下fft负频谱对应的视在频率减去fs/2即可得到频谱对应的真实负频率。

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

结论：

1.如果希望绘制的频谱图的频率范围为：0-fs，则无需进行fftshift，正频率对应0-fs/2；大于fs/2的频谱的频率值为对应[-fs/2  , 0 ]负频率f + fs，注意f是负频率，是个负数。

2.如果期望绘制的幅频图的频率范围为-fs/2~fs/2，则需要运行fftshift变换，如果不变换，图示的响应频点会发生变换。

二.复信号情况

1）复信号没有负频率，以fs为采样速率的信号，fft的频谱结果是从[0,fs]的。

2）在 f> fs/2时，对复信号的fft结果进行fftshift会产生频率混叠(将下面的示例2中的频率从f=15改为f=85可以验证f=85的谱线在fftshift后跑到 f= -15 = 85 - fs = 85 - 100的位置了)，所以复信号也一般要求 f <= fs/2

3）在对雷达的慢时间维(复信号)进行fft后，由于要用doppler= ((0:LFFT-1)/LFFT  - 0.5)*PRF; 计算多普勒频率，所以对该慢时间信号fft后要fftshift下，以便和正确的频率单元相对应。注意多普勒频率fd < = PRF/2 时才测的准！

%=====================================================================================================================================

补充：

%====================================================================================================================================

%关于fftshift的程序理解
clc;close all;clear all;
fs=100;N=256;   %采样频率和数据点数
n=0:N-1;t=n/fs;   %时间序列,从0到2.55s
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号
y1=fft(x,N);      %对信号进行快速Fourier变换，256点DFT
y2=fftshift(y1);  %fftshift的操作是将fft结果以fs/2为中心左右互换
mag1=abs(y1);     %求得Fourier变换后的振幅
mag2=abs(y2);   
f1=n*fs/N;    %频率序列
f2=n*fs/N-fs/2; %频率序列向左移fs/2
figure;
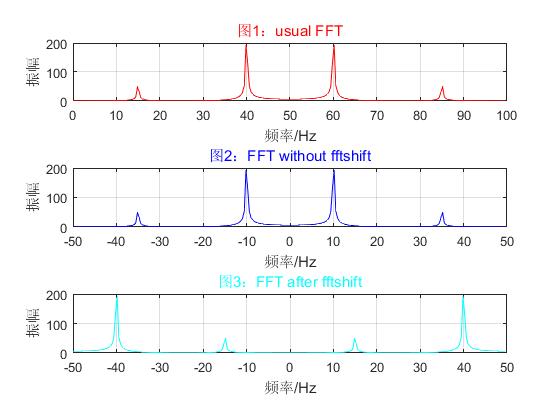
subplot(3,1,1),plot(f1,mag1,'r');  %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('图1：usual FFT','color','r');grid on;
subplot(3,1,2),plot(f2,mag1,'b');  %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('图2：FFT without fftshift','color','b');grid on;
subplot(3,1,3),plot(f2, mag2,'c');  %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('图3：FFT after fftshift','color','c');grid on;

%===============================================================================================================================

%复信号的情况：
fs=100;N=256;   %采样频率和数据点数
n=0:N-1;t=n/fs;   %时间序列
x=0.5*exp(j*2*pi*15*t)+2*exp(j*2*pi*40*t); %信号
y1=fft(x,N);    %对信号进行快速Fourier变换
y2=fftshift(y1);
mag1=abs(y1);     %求得Fourier变换后的振幅
mag2=abs(y2);   
f1=n*fs/N;    %频率序列
f2=n*fs/N-fs/2;
figure;
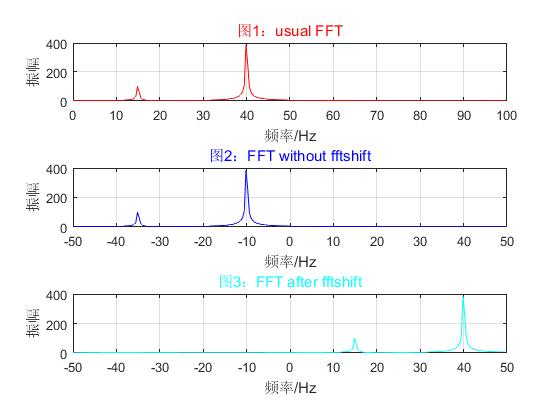
subplot(3,1,1),plot(f1,mag1,'r');  %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('图1：usual FFT','color','r');grid on;
subplot(3,1,2),plot(f2,mag1,'b');  %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('图2：FFT without fftshift','color','b');grid on;
subplot(3,1,3),plot(f2,mag2,'c');   %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('图3：FFT after fftshift','color','c');grid on;

%=============================================================================================

更直观的程序：

t=0:0.001:2;
n=2001;
Fs=1000;
Fc=200;
x=cos(2*pi*Fc*t);
y1=fft(x);
y2=fftshift(y1);
f=(0:2000)*Fs/n-Fs/2;
figure;
hold on;
plot(f,abs(y1),'r')
plot(f,abs(y2),'b')

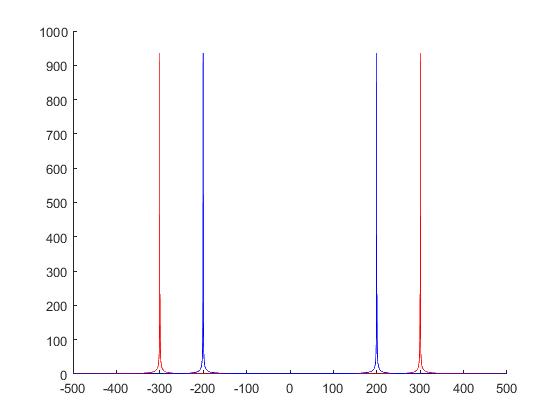
总之用fftshift后频率序列要减去fs/2

参考：

http://www.cnblogs.com/limanjihe/p/10014142.html

fft后为什么要fftshift：        https://blog.csdn.net/ssdxiao01/article/details/6687721

https://blog.csdn.net/zhyoulun/article/details/12859339

https://wenku.baidu.com/view/c6a7964476c66137ee06199a.html