Codeforces 1000G Two-Paths 树形动态规划 LCA

原文链接https://www.cnblogs.com/zhouzhendong/p/9246484.html

题目传送门 - Codeforces 1000G Two-Paths

题意

　　给定一棵有 $n(2\leq n\leq 3\times 10^5)$ 个节点的树，其中节点 $i$ 有权值 $a_i$，边 $e$ 有权值 $w_e$。$(1\leq a_i,w_e\leq 10^9)$

　　现在给出 $q(1\leq q\leq 4\times 10^5)$ 组询问，每组询问给定两个数 $x,y(1\leq x,y\leq n)$。

　　如果一条路径的起点和终点分别为 $x$ 和 $y$，而且这条路径重复经过同一条边最多 $2$ 次（点可以多次经过），那么这条路径合法。

　　一条合法路径 $P$ 的价值为 $Pr(p)$。$\text{Pr}(p) = \sum\limits_{v \in \text{distinct vertices in } p}{a_v} - \sum\limits_{e \in \text{distinct edges in } p}{k_e \cdot w_e}$。

　　其中 $k_e$ 为路径 $p$ 经过 $e$ 的次数。

　　每次询问问所有合法路径的最大价值。

题解

　　我们来跑一下树形dp。

　　求出以下值。（下面是示意图，有填色的部分表示被计算）

　　其中 $dp1,dp2,f1,sum$ 都表示所取的部分的合法最大值。

　　

　　　　

　　

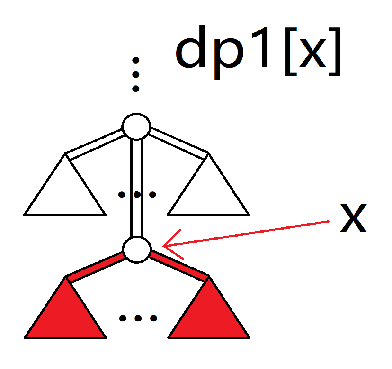
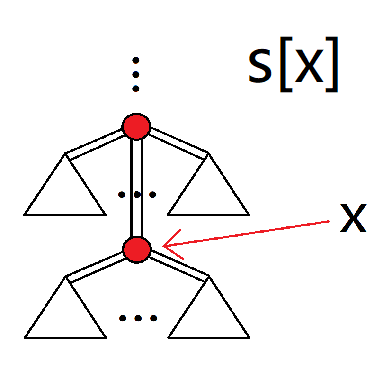
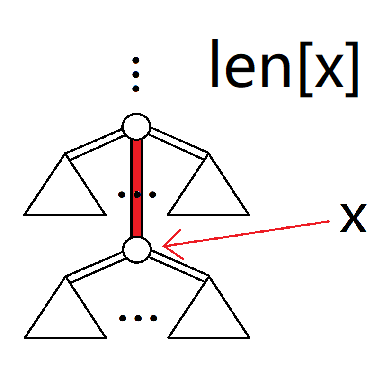
　　再描述一下上面六个量的意义：

　　dp1[x]：往 $x$ 的后代节点走最多可以赚多少。

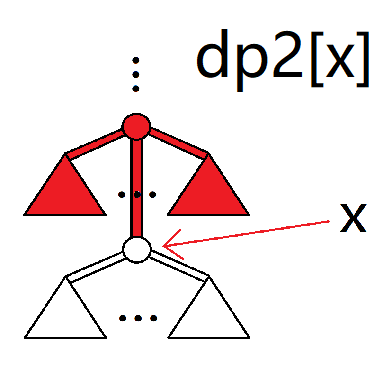
　　dp2[x]：往 $x$ 的祖先走最多可以赚多少。

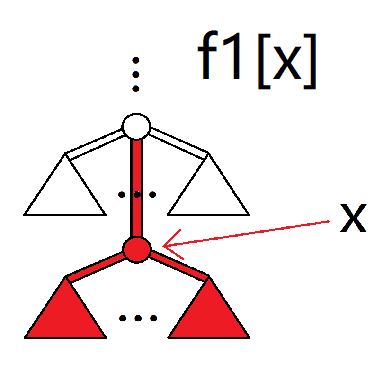
　　f1[x]：从 $x$ 的祖先向 $x$ 走最多可以赚多少。

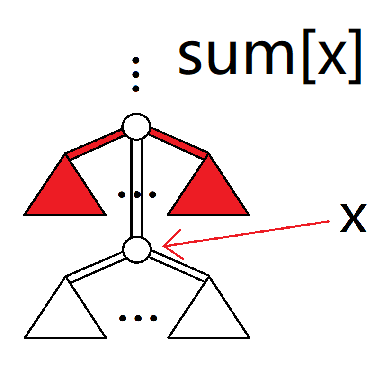
　　sum[x]：令树根到 $x$ 父亲的链为主链，假设主链上行走没有任何消耗和获益，向主链走最多可以获益多少。

　　len[x]：$x$ 到根的距离（带边权）。

　　s[x]：$x$ 的深度。

　　

　　在回答询问 $x,y$ 的时候，首先从 $x$ 到 $y$ 的路径一定被选，其中的边一定只走一次。

　　其他的我们根据之前维护的量分类讨论加加减减一下就可以了。

　　详见代码。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=300005,M=N*2;
LL read(){
	LL x=0;
	char ch=getchar();
	while (!('0'<=ch&&ch<='9'))
		ch=getchar();
	while ('0'<=ch&&ch<='9')
		x=x*10+ch-48,ch=getchar();
	return x;
}
struct Gragh{
	int cnt,y[M],nxt[M],fst[N];
	LL z[M];
	void clear(){
		cnt=0;
		memset(fst,0,sizeof fst);
	}
	void add(int a,int b,LL c){
		y[++cnt]=b,z[cnt]=c,nxt[cnt]=fst[a],fst[a]=cnt;
	}
}g;
int n,q,fa[N][20],depth[N],xx,yy;
LL a[N],dp1[N],f1[N],dp2[N],sum[N],fadis[N],len[N],s[N];
void dfs1(int x,int pre,int d,LL L){
	fa[x][0]=pre;
	depth[x]=d;
	len[x]=L;
	s[x]=s[pre]+a[x];
	for (int i=1;i<20;i++)
		fa[x][i]=fa[fa[x][i-1]][i-1];
	dp1[x]=0;
	for (int i=g.fst[x];i;i=g.nxt[i]){
		int y=g.y[i];
		LL z=g.z[i];
		if (y!=pre){
			dfs1(y,x,d+1,L+z);
			fadis[y]=z;
			f1[y]=max(dp1[y]+a[y]-z*2,0LL);
			dp1[x]+=f1[y];
		}
	}
}
void dfs2(int x,int pre,LL v,LL v2){
	dp2[x]=v;
	sum[x]=v2;
	for (int i=g.fst[x];i;i=g.nxt[i]){
		int y=g.y[i];
		LL z=g.z[i];
		if (y!=pre){
			LL _v=max(v+a[x]+dp1[x]-f1[y]-2*z,0LL);
			LL _v2=max(v2+dp1[x]-f1[y],0LL);
			dfs2(y,x,_v,_v2);
		}
	}
}
int LCA(int x,int y){
	if (depth[x]<depth[y])
		swap(x,y);
	for (int i=19;i>=0;i--)
		if (depth[x]-(1<<i)>=depth[y])
			x=fa[x][i];
	if (x==y)
		return x;
	for (int i=19;i>=0;i--)
		if (fa[x][i]!=fa[y][i])
			x=fa[x][i],y=fa[y][i];
	xx=x,yy=y;
	return fa[x][0];
}
int main(){
	scanf("%d%d",&n,&q);
	for (int i=1;i<=n;i++)
		a[i]=read();
	g.clear();
	for (int i=1;i<n;i++){
		int a=read(),b=read();
		LL c=read();
		g.add(a,b,c);
		g.add(b,a,c);
	}
	dfs1(1,0,0,0);
	dfs2(1,0,0,0);
	while (q--){
		int x,y,lca;
		scanf("%d%d",&x,&y);
		if (depth[x]>depth[y])
			swap(x,y);
		lca=LCA(x,y);
		if (x==lca){
			if (y==lca){
				printf("%I64d\n",dp1[x]+dp2[x]+a[x]);
				continue;
			}
			LL ans=s[y]-s[x]+a[x];
			ans-=len[y]-len[x];
			ans+=sum[y]-sum[x];
			ans+=dp2[x]+dp1[y];
			printf("%I64d\n",ans);
			continue;
		}
		LL ans=s[x]+s[y]-s[lca]*2+a[lca];
		ans-=len[x]+len[y]-len[lca]*2;
		ans+=sum[x]+sum[y]-sum[xx]-sum[yy];
		ans+=dp1[lca]-f1[xx]-f1[yy];
		ans+=dp2[lca]+dp1[x]+dp1[y];
		printf("%I64d\n",ans);
	}
	return 0;
}