Lingo求解线性规划案例3——混料问题

凯鲁嘎吉 - 博客园

http://www.cnblogs.com/kailugaji/

 某糖果厂用原料A、B和C按不向比率混合加工而成甲、乙、丙三种糖果(假设混合加工中不损耗原料)。原料A、B、C在糖果甲、乙、丙中的含量、原料成本、加工成本、原料限量及糖果售价如表所示。

  问该厂对这三种糖果各生产多少公斤，使得到的利润最大?

含量(%)		j号糖果			原料供应量 ai(公斤)	成本(元／公斤)
		甲(1号)	乙(2号)	丙(3号)
i号原料	A(1号)	≥60％	≥15％		2000	2.50
	B(2号)				2500	2.00
	C(3号)	≤20％	≤60％	≤70％	2200	1.70
加工成本(元／公斤)		2.00	1.80	1.60
售价(元／公斤)		12	10	8

解:设i号原料在j号糖果中的用量为xij公斤。

显然，j号糖果的产量为x1j+x2j+x3j

根据原料供应量情况，有约束条件

    xi1+xi2+xi3≤ai  i=1，2，3。

根据各种原料在各类糖果中的含量要求，有约束条件：

    x11≥0.6(x11+x2l+x31)

    x3l≤0.2(xll+x2l+x31)

    x12≥0.15(x12+x12+x32)

    x32≤0.6(x12+x22+x32)

    x33≤0.7(x13+x23+x33)

又知原料成本为

糖果加工成本为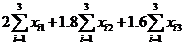

糖果出售收入为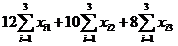

经过整理，本问题的线性规划模型为

max=10*(x11+x21+x31)+8.2*(x12+x22+x32)+6.4*(x13+x23+x33)-2.5*(x11+x12+x13)-2*(x21+x22+x23)-1.7*(x31+x32+x33);
x11>0.6*(x11+x21+x31);
x12>0.15*(x12+x22+x32);
x31<0.2*(x21+x31+x11);
x32<0.6*(x12+x22+x32);
x33<0.7*(x13+x23+x33);
x11+x12+x13<2000;
x21+x22+x23<2500;
x31+x32+x33<2200;
y1=x11+x21+x31;
y2=x12+x22+x32;
y3=x13+x23+x33;
end

结果为：

Global optimal solution found.
  Objective value:                              45180.00
  Infeasibilities:                              0.000000
  Total solver iterations:                             5

                       Variable           Value        Reduced Cost
                            X11        1326.667            0.000000
                            X21        442.2222            0.000000
                            X31        442.2222            0.000000
                            X12        673.3333            0.000000
                            X22        2057.778            0.000000
                            X32        1757.778            0.000000
                            X13        0.000000            5.200000
                            X23        0.000000            1.200000
                            X33        0.000000            1.200000
                             Y1        2211.111            0.000000
                             Y2        4488.889            0.000000
                             Y3        0.000000            0.000000

                            Row    Slack or Surplus      Dual Price
                              1        45180.00            1.000000
                              2        0.000000           -4.000000
                              3        0.000000           -4.000000
                              4        0.000000            0.000000
                              5        935.5556            0.000000
                              6        0.000000            0.000000
                              7        0.000000            9.100000
                              8        0.000000            5.600000
                              9        0.000000            5.900000
                             10        0.000000            0.000000
                             11        0.000000            0.000000
                             12        0.000000            0.000000