矩阵怪 - 2024全新矩阵产品，一键分发抖音，快手，视频号，B站，小红书！

1. 本方案面向谁，解决了什么问题
   
   本方案主要面向C端客户，特别是那些在各大短视频平台（如小红书、抖音、视频号、快手、B站等）上进行内容创作和分发的个人用户、自由职业者、小型团队或企业。这些用户通常面临着在多个平台上同时发布和管理视频内容的挑战。本方案旨在解决以下问题：

多平台视频分发繁琐：传统的方式需要用户在不同的平台上逐一发布视频，耗费大量时间和精力。

内容创作效率低：用户需要不断为不同平台创作适配的文案和视频内容，难以保持创作效率。

创新能力不足：数字人视频和AI文案生成技术的缺乏，限制了用户的内容创作能力。

本方案通过自动化、智能化的工具，帮助用户提高视频内容在多个平台上的发布效率，并提升创作灵感和创新能力。

1. 相比于市场常规方案，本方案有哪些特点
   
   与市场上现有的常规视频发布和内容创作工具相比，本方案有以下独特优势：

全域平台支持：本方案支持多种短视频平台的矩阵式管理，包括但不限于小红书、抖音、视频号、快手、B站等，还可以根据客户需求定制其他平台的接入。这种全面覆盖的能力使得用户可以一站式管理所有平台的内容分发，显著提高效率。

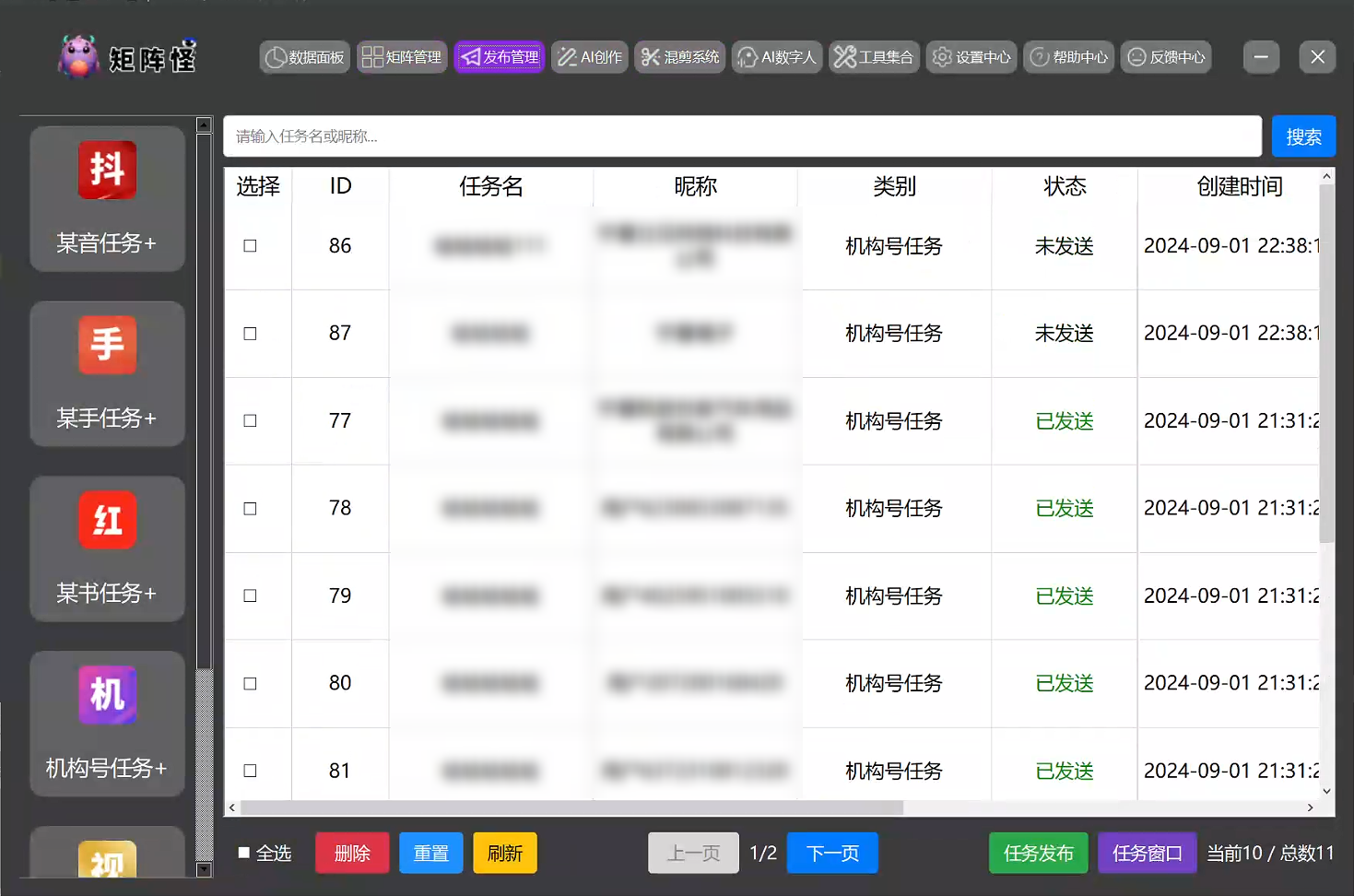
AI创作功能：内置AI文案生成工具，可以根据用户的需求自动生成高质量的文案，从而减少内容创作的时间和成本。此外，AI技术还能辅助用户更好地适配不同平台的内容要求，提高内容的点击率和传播效果。

数字人视频生成：方案还提供数字人视频制作功能，用户可以通过简单的操作生成个性化的数字人视频，使得视频内容更具创意和吸引力。这一功能在市场上仍属于创新技术，能够帮助用户在竞争中脱颖而出。

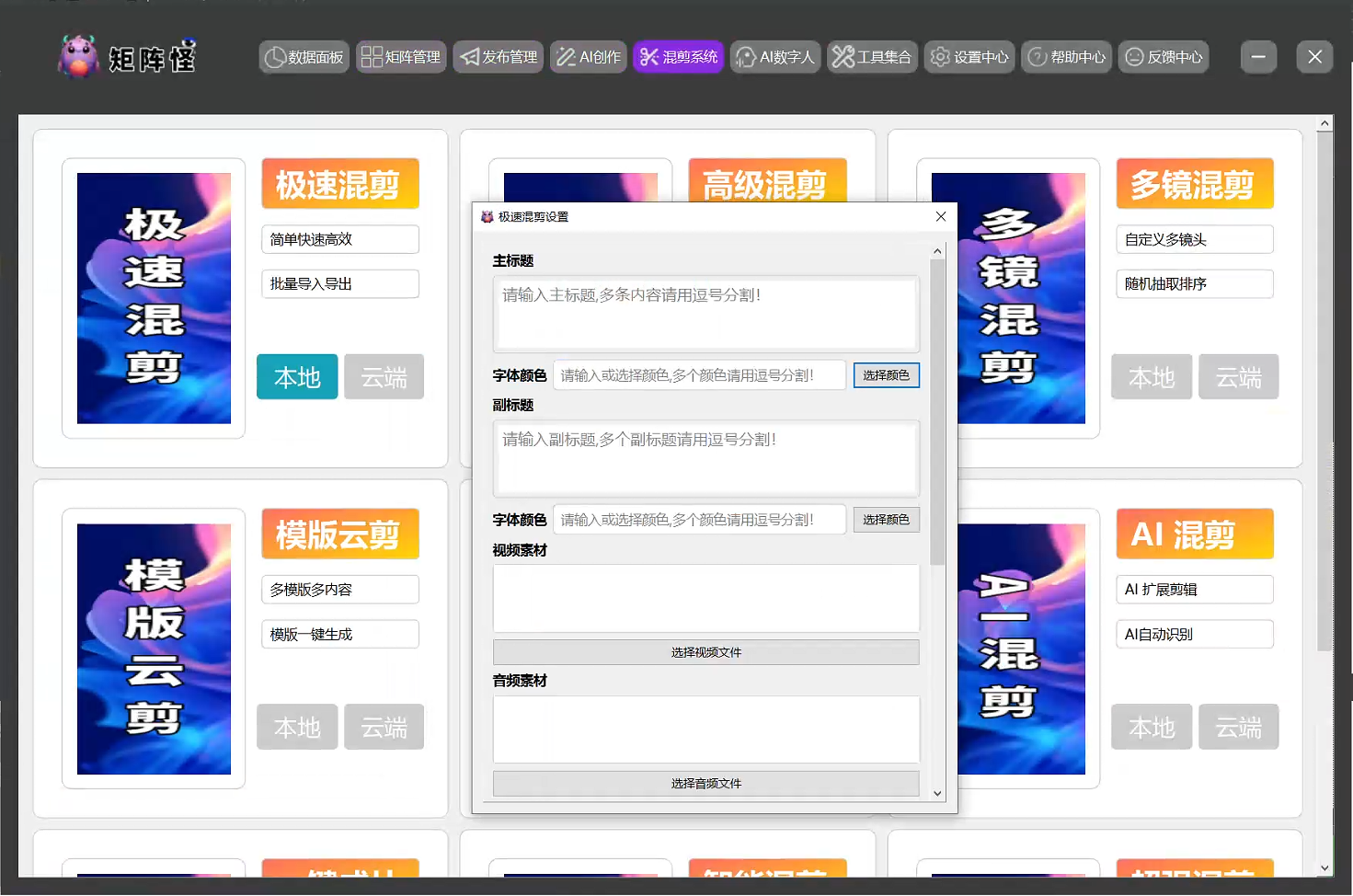
自动化视频分发：利用Python Selenium技术，本方案实现了视频内容的自动化分发，用户只需一次操作，即可在多个平台上同步发布内容。相比于传统手动发布的方式，这一功能大幅降低了操作复杂度，节省了时间。

1. 方案的产品组成或技术选型

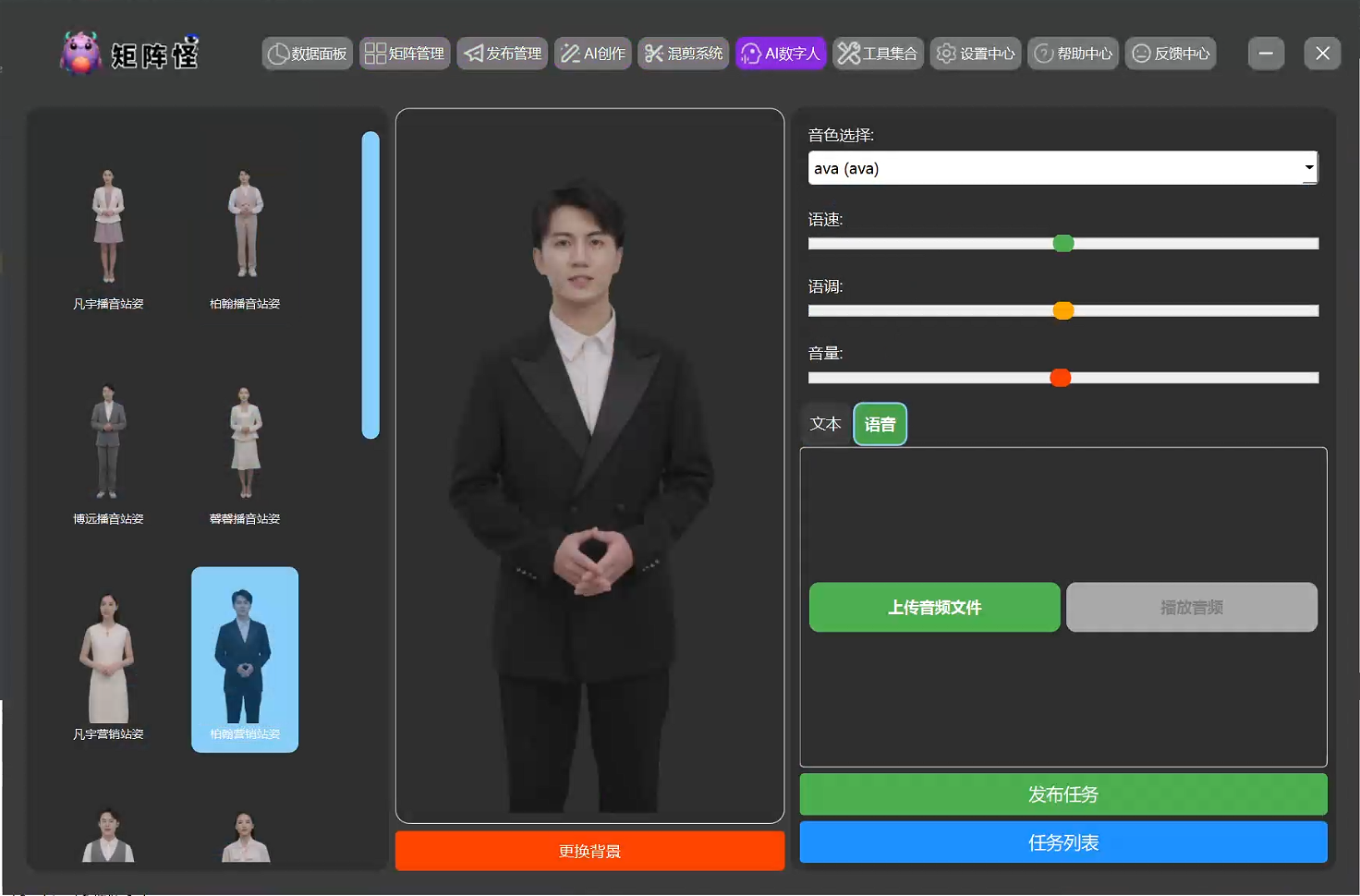
本方案的软件端采用了以下技术组成和选型：

前端技术：使用Python Selenium实现了多平台自动化操作，确保视频内容能够快速、高效地分发至各大短视频平台。

后端技术：后端采用PHP技术框架，负责处理用户请求、管理业务逻辑、数据交互等功能，确保系统的稳定性和扩展性。

数据库：采用MySQL数据库，负责存储用户数据、视频内容和发布记录，具备良好的数据存储和查询性能，能够支持大规模用户的并发操作。

AI与数字人技术：引入AI技术用于文案生成，并结合数字人技术，提供创新的内容创作工具，让用户可以通过简单操作实现高质量、个性化的视频内容制作。

通过这些技术选型和产品功能的组合，本方案不仅能为用户提供高效的多平台视频分发工具，还能提升用户的内容创作能力，帮助他们在短视频领域获得更大的成功。