U562068 - 经典多米诺

解析

首先我们需要对多米诺问题2专门进行研究得到一些性质

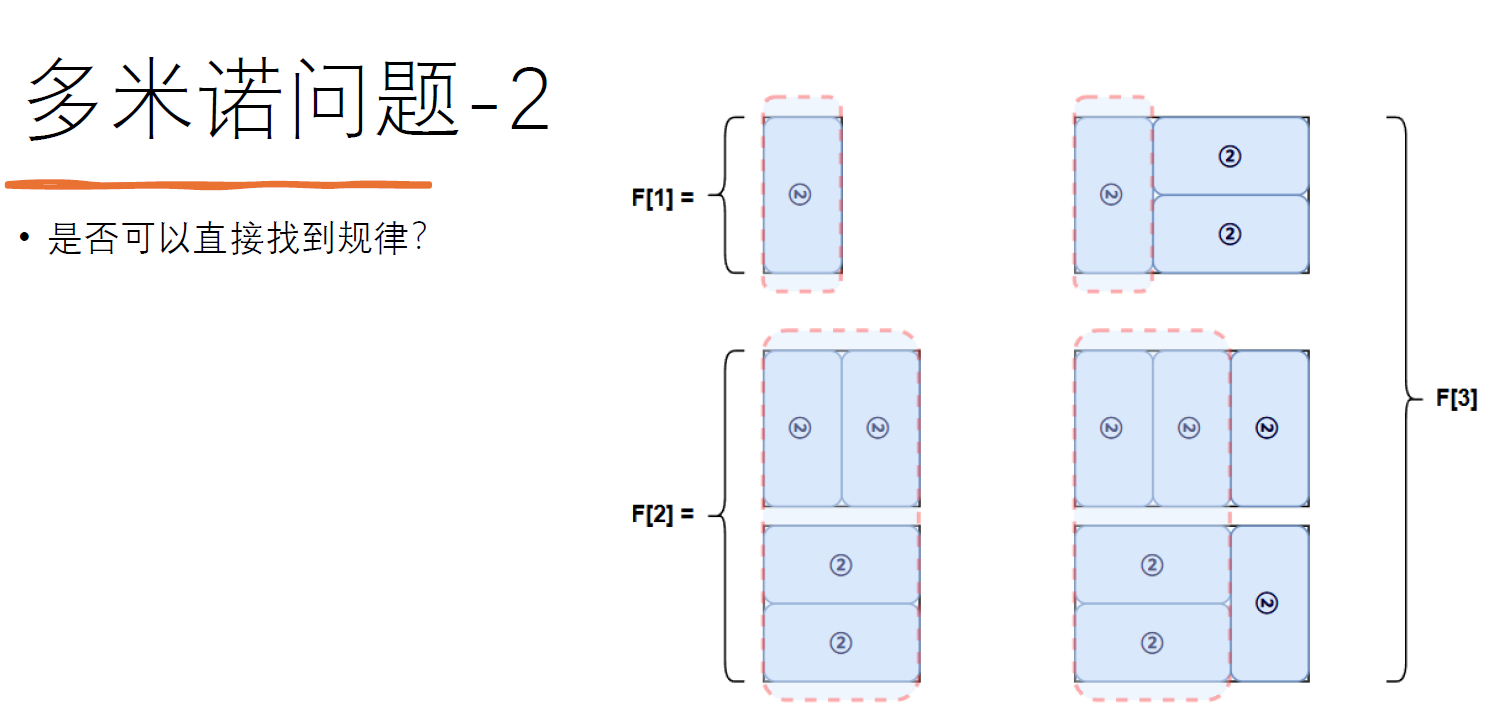
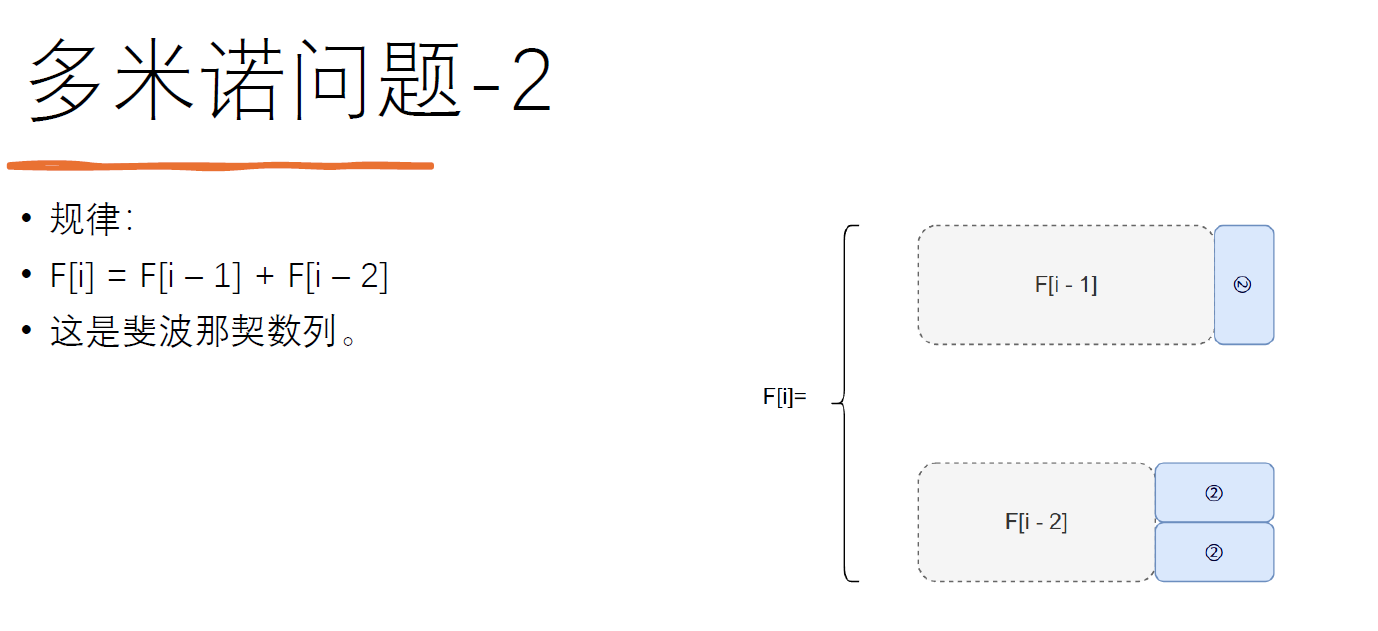
所以对于答案本身，如果不存在障碍物，那么总方案的数值就一定是一个斐波那契数。

假设如果存在障碍会有什么情况，首先障碍一定是偶数个，不然放置奇数个的话，整体的方案是一定为0的，和题意不符。

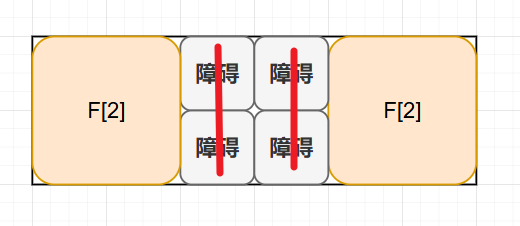
下图有两种障碍的放置方法

如果是横向放着，我们会发现，障碍的底下只能用红色横线的方法，答案固定，现在整体方案变成了左侧的方案数 乘以 右侧的方案数量。

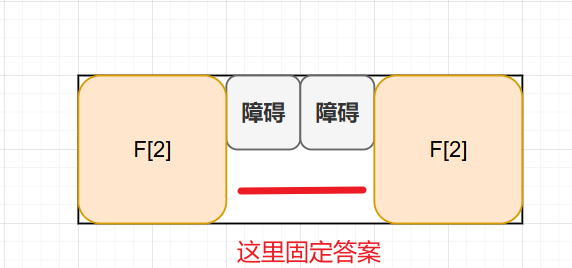
或者是竖着放置，整体方案也是变成了左侧的方案数 乘以 右侧的方案数量。

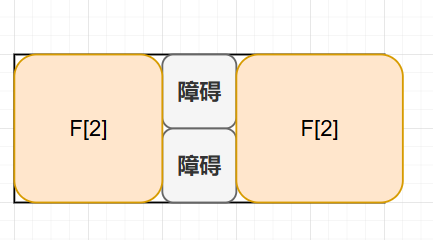
长度 \(n\) 要求最小，所以一定是竖着放置障碍，另外多列障碍和一列障碍，对方案数影响是一样的。

所以题意转换为

m是方案数，等于多个斐波那契数相乘，比如现在得到的是dp[A] 乘以 dp[B] 乘以 dp[C], 最小长度就是 A + 1 + B + 1 + C, 其中1代表竖着的一列障碍， 如下图

所以考虑用搜索将一个 \(m\) 变成多个斐波那契数相乘，找到最优解。

这里需要注意的一点是，第 \(88\) 个斐波那契数已经大于 \(1e18\) ，所以枚举范围限定在 \(1 \sim 87\) 之间， \(1\) 答案需要特殊判断。

这里可以利用最优性剪枝，和有效性剪枝，每次枚举的斐波那契数大于等于之前的，并且不能大于已有的答案。

这里提供搜索剪枝和记忆化搜索两种写法。

记忆化搜索参照：

搜索剪枝参照：