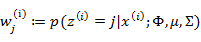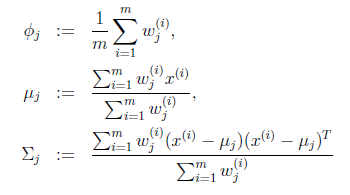混合高斯模型(Mixtures of Gaussians)
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation)。
与k-means一样,给定的训练样本是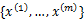 ,我们将隐含类别标签用
,我们将隐含类别标签用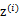 表示。与k-means的硬指定不同,我们首先认为
表示。与k-means的硬指定不同,我们首先认为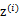 是满足一定的概率分布的,这里我们认为满足多项式分布,
是满足一定的概率分布的,这里我们认为满足多项式分布,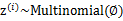 ,其中
,其中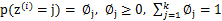 ,
,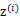 有k个值{1,…,k}可以选取。而且我们认为在给定
有k个值{1,…,k}可以选取。而且我们认为在给定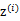 后,
后,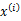 满足多值高斯分布,即
满足多值高斯分布,即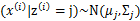 。由此可以得到联合分布
。由此可以得到联合分布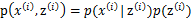 。
。
整个模型简单描述为对于每个样例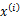 ,我们先从k个类别中按多项式分布抽取一个
,我们先从k个类别中按多项式分布抽取一个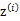 ,然后根据
,然后根据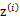 所对应的k个多值高斯分布中的一个生成样例
所对应的k个多值高斯分布中的一个生成样例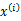 ,。整个过程称作混合高斯模型。注意的是这里的
,。整个过程称作混合高斯模型。注意的是这里的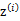 仍然是隐含随机变量。模型中还有三个变量
仍然是隐含随机变量。模型中还有三个变量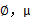 和
和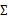 。最大似然估计为
。最大似然估计为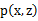 。对数化后如下:
。对数化后如下:
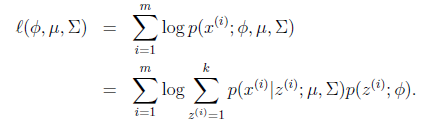
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的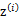 ,那么上式可以简化为:
,那么上式可以简化为:
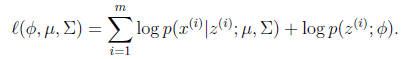
这时候我们再来对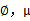 和
和 进行求导得到:
进行求导得到:
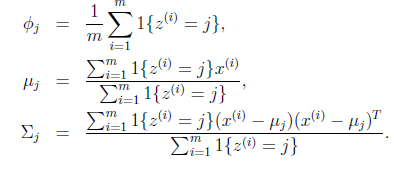
 就是样本类别中
就是样本类别中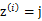 的比率。
的比率。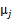 是类别为j的样本特征均值,
是类别为j的样本特征均值,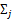 是类别为j的样例的特征的协方差矩阵。
是类别为j的样例的特征的协方差矩阵。
实际上,当知道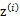 后,最大似然估计就近似于高斯判别分析模型(Gaussian discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
后,最大似然估计就近似于高斯判别分析模型(Gaussian discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了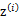 ,实际上
,实际上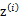 是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
|
循环下面步骤,直到收敛: { (E步)对于每一个i和j,计算
(M步),更新参数:
} |
在E步中,我们将其他参数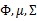 看作常量,计算
看作常量,计算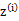 的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,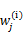 值又不对了,需要重新计算,周而复始,直至收敛。
值又不对了,需要重新计算,周而复始,直至收敛。
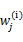 的具体计算公式如下:
的具体计算公式如下:
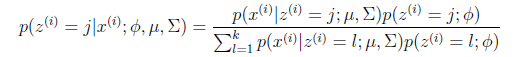
这个式子利用了贝叶斯公式。
这里我们使用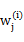 代替了前面的
代替了前面的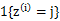 ,由简单的0/1值变成了概率值。
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别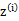 是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
虽然之前再K-means中定性描述了EM的收敛性,仍然没有定量地给出,还有一般化EM的推导过程仍然没有给出。下一篇着重介绍这些内容。
混合高斯模型(Mixtures of Gaussians)的更多相关文章
- 混合高斯模型(Mixtures of Gaussians)和EM算法
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation). 与k-means一样,给定的训练样本是,我们将隐含类别标签用表示 ...
- 混合高斯模型的EM求解(Mixtures of Gaussians)及Python实现源代码
今天为大家带来混合高斯模型的EM推导求解过程. watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQveHVhbnl1YW5zZW4=/font/5a6L5L2T/ ...
- <转>与EM相关的两个算法-K-mean算法以及混合高斯模型
转自http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html http://www.cnblogs.com/jerrylead/ ...
- EM相关两个算法 k-mean算法和混合高斯模型
转自http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html http://www.cnblogs.com/jerrylead/ ...
- 混合高斯模型(GMM)推导及实现
作者:桂. 时间:2017-03-20 06:20:54 链接:http://www.cnblogs.com/xingshansi/p/6584555.html 声明:欢迎被转载,不过记得注明出处哦 ...
- PRML读书会第九章 Mixture Models and EM(Kmeans,混合高斯模型,Expectation Maximization)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:10:56 今天的主要内容有k-means.混合高斯模型. EM算法.对于k-me ...
- Opencv混合高斯模型前景分离
#include "stdio.h" #include "string.h" #include "iostream" #include &q ...
- 混合高斯模型:opencv中MOG2的代码结构梳理
/* 头文件:OurGaussmix2.h */ #include "opencv2/core/core.hpp" #include <list> #include&q ...
- [zz] 混合高斯模型 Gaussian Mixture Model
聚类(1)——混合高斯模型 Gaussian Mixture Model http://blog.csdn.net/jwh_bupt/article/details/7663885 聚类系列: 聚类( ...
随机推荐
- 【Servlet】关于RequestDispatcher的原理
RequestDispatcher简介 RequestDispatcher 代表请求的派发者.它有2个动作:forward 和 include .客户端对于任何一个请求,可以根据业务逻辑需要,选择不同 ...
- 理解 ARC 下的循环引用
本文由 伯乐在线 - nathanw 翻译,dopcn 校稿.未经许可,禁止转载!英文出处:digitalleaves.com.欢迎加入翻译组. ARC 下的循环引用类似于日本的 B 级恐怖片.当你刚 ...
- background-size:100% 100% 时 background-position: % 失效
背景知识: background-size background-position 难题: background-size 为 100% 100% 时,background-position 部分失效 ...
- ArchLinux 添加国内镜像源
$ vim /etc/pacman.d/mirrorlist # 在最前面添加一行,这样就成功添加了网易的源: Server = http://mirrors.163.com/archlinux/$r ...
- Python面向对象之字段
类成员: 字段,方法,属性 属性是在一个函数方法前面加一个装饰器,伪造成为一个字段,调用的时候不需要加括号() 目的是把一个方法伪造成为一个字段,属性也是方法的一种,对这个方法进行改造就可以以 字段的 ...
- hdu4513完美队形II manacher
吉哥又想出了一个新的完美队形游戏! 假设有n个人按顺序站在他的面前,他们的身高分别是h[1], h[2] ... h[n],吉哥希望从中挑出一些人,让这些人形成一个新的队形,新的队形若满足以下三点要 ...
- Python模块NumPy中的tile(A,rep) 函数
from NumPy import * 函数形式: tile(A,rep) 功能:重复A的各个维度 参数类型: - A: Array类的都可以 - rep:A沿着各个维度重复的次数 这个英文单词的本意 ...
- codeforces 883H - Palindromic Cut - [字符串处理]
题目链接:http://codeforces.com/problemset/problem/883/H Time limit: 3000 ms Memory limit: 262144 kB Koly ...
- Django的视图与网址之加法计算
在最新的Django2.1中,views.py中采用的地址映射方式发生了变化,通过一个加法运算我们来看一看. 方法一:在视图views.py中定义视图逻辑,求解两个数的加法运算:c = a + b,定 ...
- iOS多线程编程之多线程简单介绍(转载)
一.进程和线程 1.什么是进程 进程是指在系统中正在运行的一个应用程序 每个进程之间是独立的,每个进程均运行在其专用且受保护的内存空间内 比如同时打开QQ.Xcode,系统就会分别启动2个进程 通过“ ...