八皇后问题的Python实现和C#实现

看到八皇后问题的解决思路， 感觉很喜欢。 我用C#实现的版本之前贴在了百度百科上（https://baike.baidu.com/item/%E5%85%AB%E7%9A%87%E5%90%8E%E9%97%AE%E9%A2%98#2_7）。百度百科已经有Python版本， 且效率比我的高一点儿， 所以决定把我的版本在博客园贴出来。相信我的版本更容易理解。 希望能够对大家有所帮助。上代码：

Python:

# EightQueens.py
def checkConflict(queenList, nextY):
    for posY in range(nextY):
        if abs(queenList[posY]-queenList[nextY])==abs(posY-nextY) or queenList[posY] == queenList[nextY]:
            return True
    return False

count = 0
def putQueen(queenCount, queenList, nextY):
    for queenList[nextY] in range(queenCount):
        if checkConflict(queenList, nextY)==False:
            nextY+=1

            if nextY < queenCount:
                putQueen(queenCount, queenList, nextY)
            else:
                global count
                count+=1
                print(str(count)+": " + ", ".join(str(pos) for pos in queenList))

            nextY-=1

# call the method
queenCount = 12
queenList = [0] * queenCount
putQueen(queenCount, queenList, 0)

C#:

// EightQueens.cs
namespace EightQueens
{
    class EightQueens
    {
        private bool checkConflict(List<int> queenList, int nextY)
        {
            for (int positionY = 0; positionY < nextY; positionY++)
            {
                if (Math.Abs(queenList[positionY] - queenList[nextY]) == Math.Abs(positionY - nextY) || queenList[positionY] == queenList[nextY])
                {
                    return true;
                }
            }
            return false;
        }

        long count = 0;
        public void putQueen(int queenCount, List<int> queenList, int nextY)
        {
            for (queenList[nextY] = 0; queenList[nextY] < queenCount; queenList[nextY]++)
            {
                if (checkConflict(queenList, nextY) == false)
                {
                    nextY++;
                    if (nextY < queenCount)
                    {
                        putQueen(queenCount, queenList, nextY);
                    }
                    else
                    {
                        count++;
                        Console.WriteLine(count.ToString() + ": " + string.Join(", ", queenList));
                    }
                    nextY--;
                }
            }
        }
    }
}

方法调用：

// Program.cs
namespace EightQueens
{
    class Program
    {
        static void Main(string[] args)
        {
            int queenCount = 12;
            List<int> queenList = new List<int>();
            for (int i = 0; i < queenCount; i++)
            {
                queenList.Add(0);
            }

            new EightQueens().putQueen(queenCount, queenList, 0);
            Console.ReadKey();
        }
    }
}

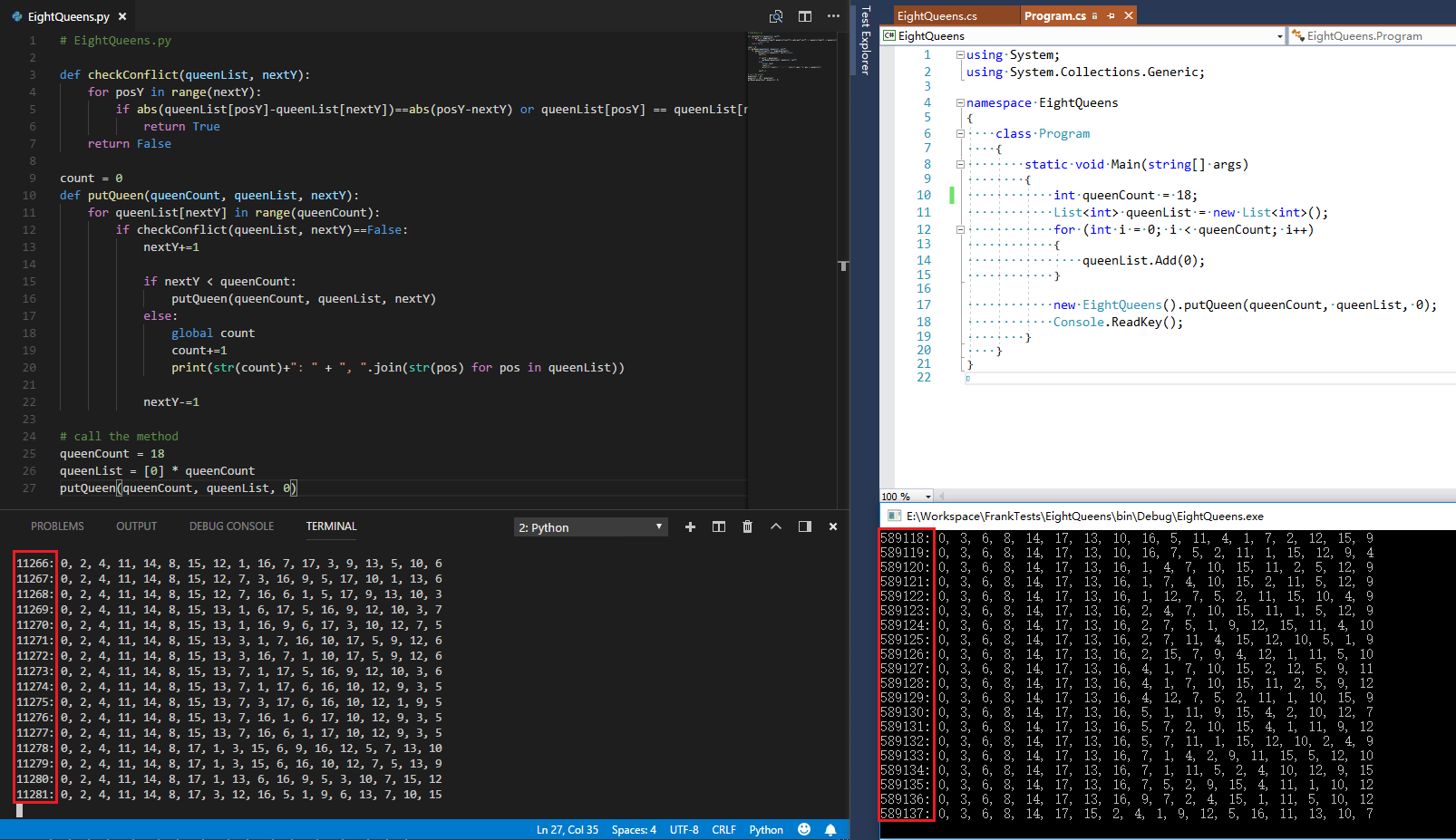
当Queen的数量越多， 可以看到Python和C#的效率差距越大。18个Queen，运行几分钟之后：