2D空间的OBB碰撞实现

OBB全称Oriented bounding box,方向包围盒算法。其表现效果和Unity的BoxCollider并无二致。由于3D空间的OBB需要多考虑一些情况

这里仅关注2D空间下的OBB。

实现效果：

网上有许多OBB的讲解，其具体步骤也未必一样，我是这么做的

在两个凸多边形中找到一根轴，凸多边形所有在这根轴上的投影点不产生相交，则这两个凸多边形不相交。

这根轴一般取每个边的垂线，逐个投影进行测试。

这里先上一个BOX的版本，如下图：

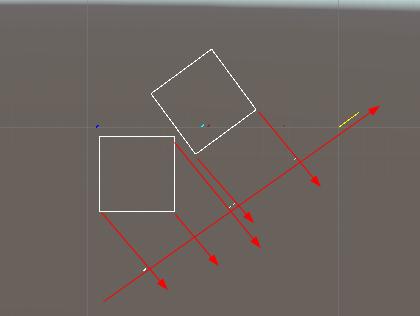
可以看见在右侧方块的投影轴上，得到了非相交结果

Box版本代码如下：

using UnityEngine;

public class OBB : MonoBehaviour
{
    public bool enableDebug;
    public int debug_axisIndex;
    int mDebugInternalAxisIndex;

    public Vector2 size;

    public Color gizmosColor = Color.white;

    Vector2 P0 { get { return transform.localToWorldMatrix.MultiplyPoint3x4(-size * 0.5f); } }
    Vector2 P1 { get { return transform.localToWorldMatrix.MultiplyPoint3x4(new Vector3(size.x * 0.5f, -size.y * 0.5f, )); } }
    Vector2 P2 { get { return transform.localToWorldMatrix.MultiplyPoint3x4(size * 0.5f); } }
    Vector2 P3 { get { return transform.localToWorldMatrix.MultiplyPoint3x4(new Vector3(-size.x * 0.5f, size.y * 0.5f, )); } }

    public bool Intersects(OBB other)
    {
        var axis1 = (P1 - P0).normalized;
        var axis2 = (P3 - P0).normalized;

        var axis3 = (other.P1 - other.P0).normalized;
        var axis4 = (other.P3 - other.P0).normalized;

        mDebugInternalAxisIndex = ;

        var isNotIntersect = false;
        isNotIntersect |= ProjectionIsNotIntersect(this, other, axis1);
        isNotIntersect |= ProjectionIsNotIntersect(this, other, axis2);
        isNotIntersect |= ProjectionIsNotIntersect(this, other, axis3);
        isNotIntersect |= ProjectionIsNotIntersect(this, other, axis4);

        return isNotIntersect ? false : true;
    }

    bool ProjectionIsNotIntersect(OBB x, OBB y, Vector2 axis)
    {
        var x_p0 = Vector3.Project(x.P0, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(x.P0, axis), axis));
        var x_p1 = Vector3.Project(x.P1, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(x.P1, axis), axis));
        var x_p2 = Vector3.Project(x.P2, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(x.P2, axis), axis));
        var x_p3 = Vector3.Project(x.P3, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(x.P3, axis), axis));

        var y_p0 = Vector3.Project(y.P0, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(y.P0, axis), axis));
        var y_p1 = Vector3.Project(y.P1, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(y.P1, axis), axis));
        var y_p2 = Vector3.Project(y.P2, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(y.P2, axis), axis));
        var y_p3 = Vector3.Project(y.P3, axis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(y.P3, axis), axis));

        var xMin = Mathf.Min(x_p0, x_p1, x_p2, x_p3);
        var xMax = Mathf.Max(x_p0, x_p1, x_p2, x_p3);
        var yMin = Mathf.Min(y_p0, y_p1, y_p2, y_p3);
        var yMax = Mathf.Max(y_p0, y_p1, y_p2, y_p3);

        if (enableDebug)
        {
            if (debug_axisIndex == mDebugInternalAxisIndex)
            {
                Debug.DrawRay(Vector3.Project(x.P0, axis), Vector3.one * 0.1f);
                Debug.DrawRay(Vector3.Project(x.P2, axis), Vector3.one * 0.1f);

                Debug.DrawRay(Vector3.Project(y.P0, axis), Vector3.one * 0.1f, Color.white * 0.9f);
                Debug.DrawRay(Vector3.Project(y.P2, axis), Vector3.one * 0.1f, Color.white * 0.9f);

                Debug.DrawRay(Vector3.zero, Vector3.one * 0.1f, Color.black);
                Debug.DrawRay(Vector3.zero, axis, Color.yellow);
                Debug.DrawRay(xMin * Vector3.right, Vector3.one * 0.1f, Color.blue);
                Debug.DrawRay(xMax * Vector3.right, Vector3.one * 0.1f, Color.cyan);
                Debug.DrawRay(yMin * Vector3.right, Vector3.one * 0.1f, Color.red * 0.5f);
                Debug.DrawRay(yMax * Vector3.right, Vector3.one * 0.1f, Color.red * 0.5f);

                Debug.Log("(yMin >= xMin && yMin <= xMax): " + (yMin >= xMin && yMin <= xMax) + " frame count: " + Time.frameCount);
                Debug.Log("(yMax >= xMin && yMax <= xMax): " + (yMax >= xMin && yMax <= xMax) + " frame count: " + Time.frameCount);
                Debug.Log("(xMin >= yMin && xMin <= yMax): " + (xMin >= yMin && xMin <= yMax) + " frame count: " + Time.frameCount);
                Debug.Log("(xMax >= yMin && xMax <= yMax): " + (xMax >= yMin && xMax <= yMax) + " frame count: " + Time.frameCount);
            }
            mDebugInternalAxisIndex++;
        }

        if (yMin >= xMin && yMin <= xMax) return false;
        if (yMax >= xMin && yMax <= xMax) return false;
        if (xMin >= yMin && xMin <= yMax) return false;
        if (xMax >= yMin && xMax <= yMax) return false;

        return true;
    }

    void OnDrawGizmos()
    {
        var cacheMatrix = Gizmos.matrix;
        var cacheColor = Gizmos.color;

        Gizmos.matrix = transform.localToWorldMatrix;

        Gizmos.color = gizmosColor;
        Gizmos.DrawWireCube(Vector3.zero, new Vector3(size.x, size.y, 1f));

        Gizmos.color = cacheColor;
        Gizmos.matrix = cacheMatrix;
    }
}

Obb.cs

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    public OBB a;
    public OBB b;

    void Update()
    {
        var isIntersects = a.Intersects(b);
        if (isIntersects)
        {
            a.gizmosColor = Color.red;
            b.gizmosColor = Color.red;
        }
        else
        {
            a.gizmosColor = Color.white;
            b.gizmosColor = Color.white;
        }
    }
}

Test.cs

增加了一个debug开关，可以单独查看每个轴的映射信息。

那么下面是凸多边形的版本，垂线通过叉乘获取：

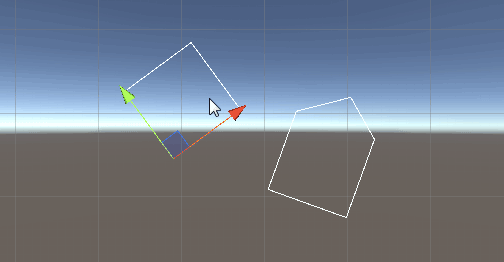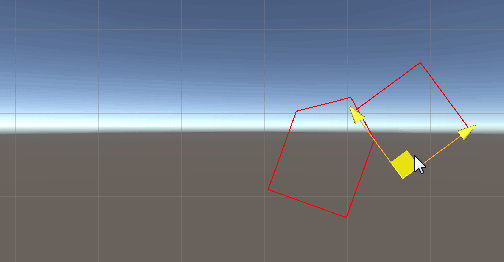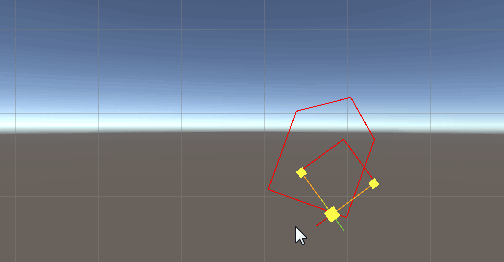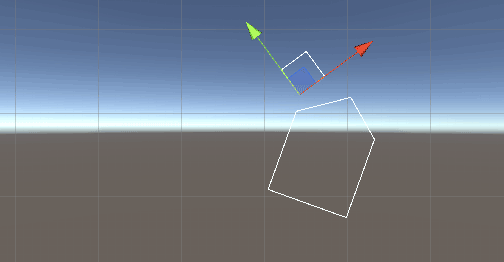
脚本如下：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class OBB : MonoBehaviour
{
    public Vector2[] points = new Vector2[];
    public int debug_Index;
    int mDebug_Index;
    public Color gizmosColor = Color.white;

    public bool Intersects(OBB other)
    {
        var isNotIntersect = false;

        mDebug_Index = ;
        for (int i = ; i <= points.Length; i++)
        {
            var p0 = transform.localToWorldMatrix.MultiplyPoint3x4(points[i - ]);
            var p1 = transform.localToWorldMatrix.MultiplyPoint3x4(points[i % points.Length]);

            var axis = Vector3.Cross((p1 - p0), Vector3.forward).normalized;
            isNotIntersect |= ProjectionIsNotIntersect(this, other, axis);

            mDebug_Index++;
        }

        return isNotIntersect ? false : true;
    }

    bool ProjectionIsNotIntersect(OBB x, OBB y, Vector2 axis)
    {
        float xMin, xMax, yMin, yMax;
        GetMinMax(x.transform.localToWorldMatrix, x.points, axis, out xMin, out xMax);
        GetMinMax(y.transform.localToWorldMatrix, y.points, axis, out yMin, out yMax);

        if (yMin >= xMin && yMin <= xMax) return false;
        if (yMax >= xMin && yMax <= xMax) return false;
        if (xMin >= yMin && xMin <= yMax) return false;
        if (xMax >= yMin && xMax <= yMax) return false;

        return true;
    }

    void GetMinMax(Matrix4x4 matrix, Vector2[] points, Vector2 projectAxis, out float min, out float max)
    {
        min = float.MaxValue;
        max = float.MinValue;

        for (int i = ; i < points.Length; i++)
        {
            var p = matrix.MultiplyPoint3x4(points[i]);

            var projectValue = Vector3.Project(p, projectAxis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(p, projectAxis), projectAxis));

            if (projectValue > max)
                max = projectValue;
        }

        for (int i = ; i < points.Length; i++)
        {
            var p = matrix.MultiplyPoint3x4(points[i]);

            var projectValue = Vector3.Project(p, projectAxis).magnitude * Mathf.Sign(Vector3.Dot(Vector3.Project(p, projectAxis), projectAxis));

            if (projectValue < min)
                min = projectValue;
        }
    }

    void OnDrawGizmos()
    {
        var cacheColor = Gizmos.color;

        Gizmos.color = gizmosColor;

        for (int i = ; i <= points.Length; i++)
        {
            var p0 = transform.localToWorldMatrix.MultiplyPoint3x4(points[i - ]);
            var p1 = transform.localToWorldMatrix.MultiplyPoint3x4(points[i % points.Length]);

            Gizmos.DrawLine(p0, p1);
        }

        Gizmos.color = cacheColor;
    }
}

OBB.cs

到这里就结束了，如果是一个具体形状和点进行比较方法其实是非常多的，而类似这样的凸包之间进行相交测试OBB倒是一个蛮实用的办法。