Linear Algebra lecture3 note
Matrix multiplication(4 ways!)
Inverse of A
Gauss-Jordan / find inverse of A
Matrix multiplication
1、点积法
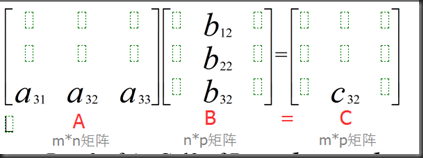
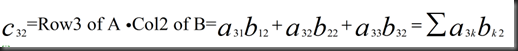
2、matrix * column=comb of columns
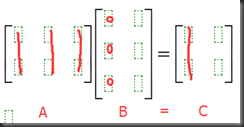
columns of C are comb of cols of A
3、matrix * row = comb of rows
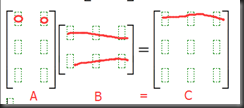
rows of C are comb of rows of B
4、matrix * matrix=comb of row*col
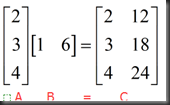
AB=sum of (cols of A )*(rows of B)
another example:
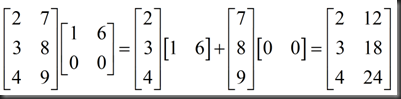
*5、Block (分块行 * 分块列)
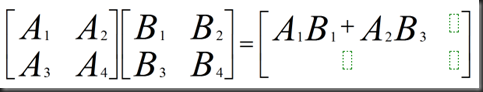
Inverses( Square matrices)
if inverse of A exits, then
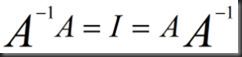
invertible, non-singular
思考如何求此矩阵的逆,矩阵及其逆应满足条件:
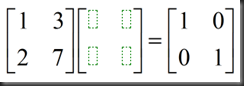
设逆矩阵由元素a,b,c,d构成,如图:
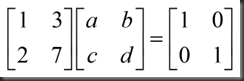
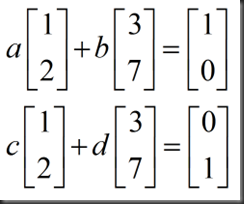
以上讨论的都是逆矩阵存在的情况,下面举例讨论逆矩阵不存在的情况(singular case,no inverse),
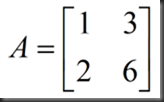
可以从以下三方面来解释:
1、行列式为0
2、假设A`存在,A中两列向量共线,所以不可能通过线性组合构成单位矩阵,AA`≠I,就没有A`的说法了
3、You can find a vector X with AX=0 (X≠0)
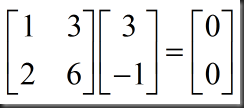
由于AX=0,假设A`存在,等式两边同时乘以A`,A`AX=A`0=0, IX=0,X=0 与 X≠0矛盾,故假设不成立
若矩阵中其中一列对线性组合毫无贡献,则矩阵不可能有逆
Gauss Jordan(solve 2 equations at once)
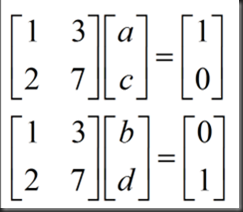
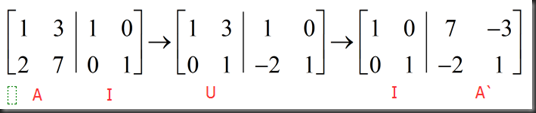
可得到A的逆矩阵形式为:

解释推导:
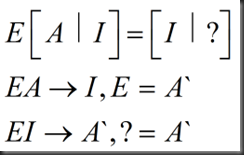
Linear Algebra lecture3 note的更多相关文章
- Linear Algebra lecture1 note
Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06 Lecture 1 ...
- Linear Algebra lecture9 note
Linear independence Spanning a space Basis and dimension 以上概念都是针对a bunch of vectors, 不是矩阵里的概念 Supp ...
- Linear Algebra lecture10 note
Four fundamental subspaces( for matrix A) if A is m by n matrix: Column space C(A) in Rm (列空间在m维实 ...
- Linear Algebra lecture8 note
Compute solution of AX=b (X=Xp+Xn) rank r r=m solutions exist r=n solutions unique example: 若想方程有解 ...
- Linear Algebra lecture7 note
Computing the nullspace (Ax=0) Pivot variables-free variables Special solutions: rref( A)=R rank o ...
- Linear Algebra lecture6 note
Vector spaces and subspaces Column space of A solving Ax=b Null space of A Vector space requiremen ...
- Linear Algebra Lecture5 note
Section 2.7 PA=LU and Section 3.1 Vector Spaces and Subspaces Transpose(转置) example: 特殊情况,对称 ...
- Linear Algebra lecture4 note
Inverse of AB,A^(A的转置) Product of elimination matrices A=LU (no row exchanges) Inverse of AB,A^(A ...
- Codeforces Gym101502 B.Linear Algebra Test-STL(map)
B. Linear Algebra Test time limit per test 3.0 s memory limit per test 256 MB input standard input ...
随机推荐
- css渐变色DIV
<!DOCTYPE html> <html lang="en" xmlns="http://www.w3.org/1999/xhtml"> ...
- DateTimePicker如何与Delphi自带Style同步
Delphi 的 DateTimePicker 组件有一个CalColors属性,可以设置 DropDown 打开的日历节目的风格.但如果不使用 Delphi 自带的 Style,在这里设置属性看不到 ...
- DOM位置参数
以chrome浏览器测试为准 scrollwidth scrollheight clientwidth clientheight offsetwidth offsetheight 对象的实际宽高 包括 ...
- H5的FormData对象完成ajax上传文件multiFile
最近工作中需要完成,ajax上传图片,可是input file +ajax是无法完成的: 于是寻找了许久,发现了H5 的一个对象FormData 使用方法如下: HTML: <form id=& ...
- apache 反向代理配置
配置前资料检查: 1.可以使用的apache 安装apache服务:打开cmd , 在apache的bin目录下执行以下命令 httpd -k install -n apache2.2 其中&q ...
- Java 自定义注解
在spring的应用中,经常使用注解进行开发,这样有利于加快开发的速度. 介绍一下自定义注解: 首先,自定义注解要新建一个@interface,这个是一个注解的接口,在此接口上有这样几个注解: @Do ...
- Install and set JAVA home on MAC OS with commandline
最近需要在MAC上做一些测试,由于测试机没有安装Java,只能自己安装,由于不能通过图形化界面访问测试机,只能通过命令行的形式来安装JAVA. 1. Download the jre/jdk inst ...
- apt-get install *** 出现 软件包***没有提供可供安装的候选者
今天,重新安装Ubuntu13.04后,在命令行输入 sudo apt-get install aptitude 提示: 软件包 aptitude 没有提供可供安装的候选者 sudo apt-get ...
- 【C】二级指针探秘 & 星号的两种用法(1.与基本类型结合形成另一种类型,比如与int结合形成int* 2.取值操作)
1)问题:二级指针到底是什么?怎么用的?怎么存放的? #include <stdio.h> #define TEST_ADDR 0x12FF40 void main() { int a = ...
- 关于Python中的文件操作(转)
总是记不住API.昨晚写的时候用到了这些,但是没记住,于是就索性整理一下吧: python中对文件.文件夹(文件操作函数)的操作需要涉及到os模块和shutil模块. 得到当前工作目录,即当前Pyth ...
