BZOJ1101 & 洛谷3455：[POI2007]ZAP——题解

https://www.luogu.org/problemnew/show/3455#sub

http://www.lydsy.com/JudgeOnline/problem.php?id=1101

Description

　　FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a
，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

Input

　　第一行包含一个正整数n，表示一共有n组询问。（1<=n<= 50000）接下来n行，每行表示一个询问，每行三个
正整数，分别为a,b,d。（1<=d<=a,b<=50000）

Output

　　对于每组询问，输出到输出文件zap.out一个正整数，表示满足条件的整数对数。

Sample Input

2
4 5 2
6 4 3

Sample Output

3
2

——————————————————————————————

%%%http://hzwer.com/4205.html

因为莫比乌斯反演才学，所以都是先看神犇博客再做。

预备知识：

1.

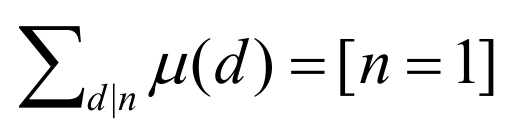
（而且hzw的博客有数学公式，我没有，所以不是特别好看，想看更加易懂的题解就戳上面吧。）

这题让你求∑∑[gcd(x,y)==d](x<=a,y<=b)的值。

显然可以化成∑∑[gcd(x,y)==1](x<=a/d,y<=b/d)

有知识1可得∑∑∑miu(c)(x<=a/d,y<=b/d,c|gcd(x,y))

又因为d|gcd(x,y)导出c|x&&c|y所以x可取值个数为a/d/c，b为b/d/c（都为整除，下同）。

所以可得∑miu(c)*a/d/c*b/d/c(c<=a/d&&c<=b/d)提取公因式得a/d/c*b/d/c*∑miu(c)。

将a/d看作整体，我们发现a/d/c又可以套用[CQOI2007]余数之和的方法分块，将复杂度减少至根号a/d。

#include<cstdio>
#include<queue>
#include<cctype>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=;
int miu[N],su[N],sum[N];
bool he[N];
void Euler(int n){
    int tot=;
    miu[]=;
    for(int i=;i<=n;i++){
    if(!he[i]){
        su[++tot]=i;
        miu[i]=-;
    }
    for(int j=;j<=tot;j++){
        if(i*su[j]>=n)break;
        he[i*su[j]]=;
        if(i%su[j]==){
        miu[i*su[j]]=;break;
        }
        else miu[i*su[j]]=-miu[i];
    }
    }
    for(int i=;i<=n;i++)sum[i]=sum[i-]+miu[i];
    return;
}
int solve(int a,int b){
    if(a>b)swap(a,b);
    int ans=,pos;
    for(int i=;i<=a;i=pos+){
    pos=min(a/(a/i),b/(b/i));
    ans+=(sum[pos]-sum[i-])*(a/i)*(b/i);
    }
    return ans;
}
int main(){
    Euler();
    int t;
    scanf("%d",&t);
    while(t--){
    int a,b,d;
    scanf("%d%d%d",&a,&b,&d);
    printf("%d\n",solve(a/d,b/d));
    }
    return ;
}