BZOJ1912 APIO2010 洛谷P3629 巡逻

Description：

在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

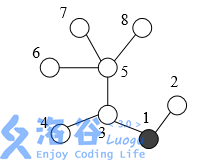
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

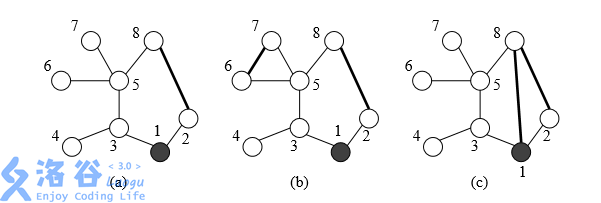
在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

Input ：

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

Output：

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

思路：K = 1时，求出树的直径L，然后把两端加一条边即可，答案就是2 * （n - 1） - L + 1

K = 2时，两个环的重叠部分会被巡逻两次，所以当求出直径L1的时候对直径上的边取反然后再求一遍直径L2就可以了（因为L2如果经过这个L1取反的部分，说明两个部分重叠，减掉L1之后重叠部分就只经过一次了，减掉（L2 - 1）相当于把重叠的部分加回来，变成“需要经过两次”），答案就是2 * (n - 1) - （L1 - 1）- （L2 - 1）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + ;

int head[N], now = ;
struct edges{
    int to,next,w;
}edge[N<<];
void add(int u ,int v, int w){ edge[++now] = {v, head[u], w}; head[u] = now;}

int n, k, dep[N], pre[N], pos1, pos2, d[N], L1, L2;
void dfs1(int x,int fa){
    for(int i = head[x]; i; i = edge[i].next){
        int v = edge[i].to;
        if(v == fa) continue;
        dep[v] = dep[x] + edge[i].w;
        dfs1(v, x);
    }
    if(dep[x] > dep[pos1])
      pos1 = x;
}
void dfs2(int x,int fa){
    for(int i = head[x]; i; i = edge[i].next){
        int v = edge[i].to;
        if(v == fa) continue;
        d[v] = d[x] + edge[i].w;
        pre[v] = i;
        dfs2(v, x);
    }
    if(d[x] > d[pos2])
      pos2 = x;
}
void work(int x){
    if(x == ) return ;
    int tmp = pre[x];
    edge[tmp].w = edge[tmp ^ ].w = -;
    work(edge[tmp ^ ].to);
}
void dp(int x, int fa){
    for(int i = head[x]; i; i = edge[i].next){
        int v = edge[i].to;
        if(v == fa) continue;
        dp(v, x);
        L2 = max(L2, d[x] + d[v] + edge[i].w);
        d[x] = max(d[x], d[v] + edge[i].w);
    }
}
int main(){
    scanf("%d%d",&n, &k);
    int x, y;
    for(int i = ; i < n; i++){
        scanf("%d%d",&x,&y);
        add(x, y, ); add(y, x, );
    }
    dfs1(, -);
    dfs2(pos1, -);
    work(pos2);
    L1 = d[pos2];
    if(k == ){
        printf("%d\n", * n - L1 - );
        return ;
    }
/*    for(x = 1; x <= n; x++){
        cout<<x<<": ";
        for(int i = head[x]; i; i = edge[i].next)
          cout<<edge[i].to<<" "<<"("<<edge[i].w<<") ";
        cout<<endl;
    }*/
    memset(d,,sizeof(d));
    dp(, -);
    printf("%d\n", * n - L1 - L2);
    return ;
}