【BZOJ3884】上帝与集合的正确用法 [欧拉定理]

上帝与集合的正确用法

Time Limit: 5 Sec  Memory Limit: 128 MB
[Submit][Status][Discuss]

Description

　　

Input

　　第一行一个T，接下来T行，每行一个正整数p，代表你需要取模的值。

Output

　　T行，每行一个正整数，为答案对p取模后的值。

Sample Input

　　3
　　2
　　3
　　6

Sample Output

　　0
　　1
　　4

HINT

　　对于100%的数据，T<=1000，p<=10^7

Solution

　　我们运用欧拉定理：

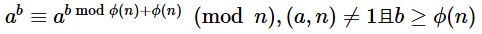
　　然后还有一个定理：一个数在执行log次操作后，值不会改变。

　　然后就可以直接求了。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const int INF = ;

 int T,x;
 int phi[ONE],pn;

 int get()
 {
         int res=,Q=;char c;
         while( (c=getchar())< || c> )
         if(c=='-')Q=-;
         res=c-;
         while( (c=getchar())>= && c<= )
         res=res*+c-;
         return res*Q;
 }

 int Quickpow(int a,int b,int MOD)
 {
         int res = ;
         while(b)
         {
             if(b & ) res = (s64)res * a % MOD;
             a = (s64)a * a % MOD;
             b >>= ;
         }
         return res;
 }

 int Getphi(int n)
 {
         int res = n;
         for(int i=; i*i<=n; i++)
         if(n % i == )
         {
             res = res/i*(i-);
             while(n % i == ) n /= i;
         }
         if(n != ) res = res/n*(n-);
         return res;
 }

 int Deal(int p)
 {
         pn = ;    phi[] = p;
         while(p != ) phi[++pn] = p = Getphi(p);
         phi[++pn] = ;

         int a = ;
         for(int i=pn; i>=; i--)
         {
             if(a >= phi[i]) a = a%phi[i] + phi[i];
             a = (s64)Quickpow(, a, phi[i-]);
             if(!a) a = phi[i-];
         }

         return a % phi[];
 }

 int main()
 {
         T = get();
         while(T--)
         {
             x = get();
             printf("%d\n", Deal(x));
         }
 }