K - Candies（最短路+差分约束）

题目大意：给N个小屁孩分糖果，每个小屁孩都有一个期望，比如A最多比B多C个，再多了就不行了，会打架的，求N最多比1多几块糖

分析：就是求一个极小极大值...试试看

这里需要用到一个查分约束的东西

下面是查分约束详解：

一直不知道差分约束是什么类型题目，最近在写最短路问题就顺带看了下，原来就是给出一些形如x-y<=b不等式的约束，问你是否满足有解的问题

好神奇的是这类问题竟然可以转换成图论里的最短路径问题，下面开始详细介绍下

比如给出三个不等式,b-a<=k1,c-b<=k2,c-a<=k3,求出c-a的最大值,我们可以把a,b,c转换成三个点，k1，k2，k3是边上的权，如图

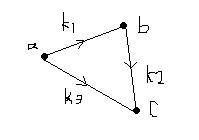
由题我们可以得知，这个有向图中，由题b-a<=k1,c-b<=k2,得出c-a<=k1+k2,因此比较k1+k2和k3的大小，求出最小的就是c-a的最大值了

根据以上的解法，我们可能会猜到求解过程实际就是求从a到c的最短路径，没错的....简单的说就是从a到c沿着某条路径后把所有权值和k求出就是c -a<=k的一个

推广的不等式约束，既然这样，满足题目的肯定是最小的k，也就是从a到c最短距离...

理解了这里之后，想做题还是比较有困难的，因为题目需要变形一下，不能单纯的算..

首先以poj3159为例,这个比较简单，就是给出两个点的最大差，然后让你求1到n的最大差，直接建图后用bellman或者spfa就可以过了

稍微难点的就是poj1364，因为他给出的不等式不是x-y<=k形式，有时候是大于号，这样需要我们去变形一下，并且给出的还是>,<没有等于，都要变形

再有就是poj1201，他要求出的是最长距离，那就要把形式变换成x-y>=k的标准形式

注意点:

1. 如果要求最大值想办法把每个不等式变为标准x-y<=k的形式,然后建立一条从y到x权值为k的边,变得时候注意x-y<k =>x-y<=k-1

如果要求最小值的话,变为x-y>=k的标准形式，然后建立一条从y到x的k边，求出最长路径即可

2.如果权值为正，用dj，spfa，bellman都可以，如果为负不能用dj，并且需要判断是否有负环，有的话就不存在

/////////////////////////////////////////////////////////////////////

队列会超时死，用栈就会过.....不要问为什么。。。。。。。为什么。。什么。。。么。。

#include<algorithm>
#include<stack>
#include<stdio.h>
#include<string.h>
#include<string>
#include<map>
#include<iostream>
using namespace std;

const int maxn = ;
const int oo = 0x3fffffff;

struct node
{
    int u, v, c, next;
}e[maxn*];
int head[maxn], dis[maxn];
bool use[maxn];

void AddAge(int u, int v, int c, int k)
{
    e[k].u = u;
    e[k].v = v;
    e[k].c = c;
    e[k].next = head[u];
    head[u] = k;
}
void spfaStack()
{
    stack<int> sta;
    sta.push();

    while(sta.size())
    {
        int i = sta.top();sta.pop();
        use[i] = false;

        for(int j=head[i]; j != ; j=e[j].next)
        {
            int u = e[j].u, v = e[j].v, c = e[j].c;

            if(dis[v] > dis[u]+c)
            {
                dis[v] = dis[u]+c;
                if(use[v] == false)
                {
                    use[v] = true;
                    sta.push(v);
                }
            }
        }
    }
}

int main()
{
    int N, M;

    while(scanf("%d%d", &N, &M) != EOF)
    {
        int i, u, v, c;

        for(i=; i<=N; i++)
            dis[i] = oo, head[i]=;
        dis[] = ;

        for(i=; i<=M; i++)
        {
            scanf("%d%d%d", &u, &v, &c);
            AddAge(u, v, c, i);
        }

        spfaStack();

        printf("%d\n", dis[N]);
    }

    return ;

}