cf D. On Sum of Fractions

http://codeforces.com/problemset/problem/397/D

题意：v(n) 表示小于等于n的最大素数，u(n)表示比n的大的第一个素数，然后求出；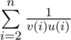

思路：把分数拆分成两个分数相减，你就会发现规律，等于1/2-1/3+1/3-1/5.。。。。。。。，找出v(n)和u(n)，答案就出来了。

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #define ll long long
 using namespace std;

 int t;
 ll n;

 ll gcd(ll a,ll b)
 {
     return b==?a:gcd(b,a%b);
 }

 int main()
 {
     scanf("%d",&t);
     while(t--)
     {
         scanf("%lld",&n);
         ll l,r;
         bool flag=true;
         for(int i=; i*i<=n; i++)
         {
             if(n%i==)
             {
                flag=false;
                break;
             }
         }
         if(flag)
         {
            r=n+;
            while(r)
            {
                int f1=;
                for(int i=; i*i<=r; i++)
                {
                    if(r%i==)
                    {
                       f1=;
                       break;
                    }
                }
                if(f1)
                {
                    break;
                }
                r++;
            }
            ll cc=*n*r;
            ll xx=n*r-*(r-);
            ll g=gcd(xx,cc);
            printf("%lld/%lld\n",xx/g,cc/g);
         }
         else
         {
            l=n-;
            while(l)
            {
               int f2=;
               for(int i=; i*i<=l; i++)
               {
                   if(l%i==)
                   {
                       f2=;
                       break;
                   }
               }
               if(f2)
               {
                   break;
               }
               l--;
            }
            r=n+;
            while(r)
            {
                int f3=;
                for(int i=; i*i<=r; i++)
                {
                    if(r%i==)
                    {
                        f3=;
                        break;
                    }
                }
                if(f3)
                {
                    break;
                }
                r++;

            }
            ll c1=*l*r;
            ll x1=l*r-*(l+r-n-);
            ll gg=gcd(x1,c1);
            printf("%lld/%lld\n",x1/gg,c1/gg);
         }
     }
     return ;
 }